结构锁解锁同步性影响因素分析

郑云青，邵济明，程芳华，刘 志

（1.上海宇航系统工程研究所，上海 201109；2.上海市空间飞行器机构重点实验室，上海 201109）

0 引言

结构锁是实现空间两飞行器刚性密封连接的主要部件之一，各锁间的运动和驱动力通过钢丝绳传递，形成锁系机构，其作用是为两飞行器提供锁紧力，保证两者刚性连接，并在对接任务完成后能同步解锁［1］。结构锁通过钢丝绳连接6套对接锁，长传动链、结构锁生产和装配的差异及工作顺序的不同，相同设计状态下结构锁钩的实际脱钩时间并不相同。首先脱钩的结构锁与最后脱钩的时间差，即结构锁解锁的同步性会直接影响两飞行器分离后的角速度。文献［2－4］分析了钢丝绳弹性变形、钢丝绳预紧力、绳轮间摩擦因数，以及锁钩间摩擦因数对结构锁同步性的影响，文献［2］定量给出了钢丝绳的弹性变形、预紧力等对同步性的影响规律；文献［3－4］明确绳轮间的摩擦因数是主要影响因素。采取文献［2－4］的控制措施后，结构锁运动的同步性得到了一定程度的改善。但上述文献分析过程中均假设同一组对接锁的性能、参数完全相同，未考虑生产、装配的差异。本文在采取上述措施的基础上，建立了结构锁解锁的力学模型，在考虑产品实际性能条件下分析了影响结构锁脱钩时间的因素，并提出了减小结构锁脱钩时间差需控制的措施。

1 结构锁工作原理

结构锁沿周向均布于对接框外侧，分为两组，每组有锁6把，其中只有1把有驱动装置（如图1所示的1＃锁），其他锁与锁间通过锁上的绳轮带动钢丝绳，经定滑轮连接到另一把结构锁的绳轮上。结构锁由主动钩组件和被动钩组件组成，运输飞船的主动钩组件与目标飞行器上对应的被动钩组件配合，而被动钩组件则安装在被预紧的碟簧组上［1］。运动时，主动钩组件由电机通过绳轮驱动偏心轴，使锁钩产生运动。锁紧时，绳轮带动偏心轴旋转，驱动主动钩在拉簧及限位板的约束下沿飞行器轴向作拉紧运动，将两飞行器拉紧；解锁时，偏心轴反转，主动钩体沿飞行器轴向作反向运动，直至偏心轴上的凸轮与偏心套上的凸轮相互作用，使主动钩体让开一定的角度，释放被动锁钩，实现解锁。主动锁钩处于解锁时的状态如图2所示［5］。

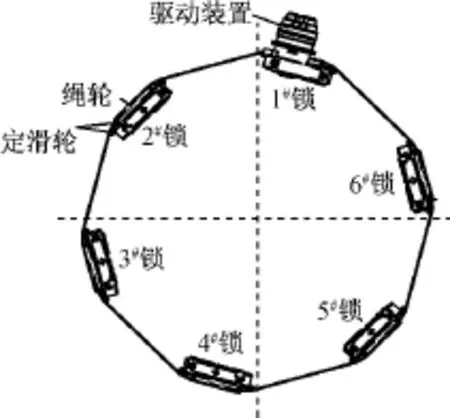
图1 一组结构锁布局Fig.1 Distributing of one group structure hooks

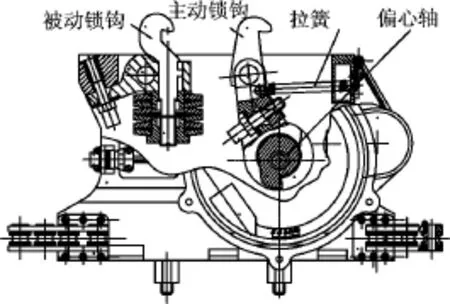
图2 结构锁（主动钩处于解锁位置）Fig.2 Schematic drawing of structure hook（active hook at released position）

2 受力分析

根据结构锁的工作原理，结构锁的解锁可分为三个阶段。

a）结构锁伸出：从结构锁的锁紧位置至结构锁处于0°位置。在该阶段，结构锁主动锁钩的销轴沿限位板直线向上运动。

b）结构锁主动锁钩被动旋转：从0°位置（如图3所示）至临界点S。在该阶段，结构锁的主动锁钩绕结构锁的旋转中心在偏心套的凸块驱动下被动旋转。

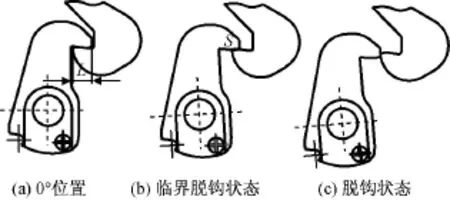
图3 主动锁钩与被动锁钩啮合状态Fig.3 Meshed state of active hook and passive hook

c）主被动锁钩自主脱离：从临界点至主被动锁钩完全分开，实现解锁。在该阶段，在主被动锁钩的相互作用下，主被动锁钩自主脱钩，实现解锁。

其中阶段b）、c）与分离有关。以下分析这两个阶段的受力。

结构锁的运动模型可简化为在XOY平面工作的曲柄滑块机构，如图4所示［6］。其中：偏心轴的偏心距为曲柄，其长度为r；偏心轴的旋转中心为曲柄的旋转中心O；主动锁销的中心为滑块的中心；限位板为滑块的滑动平面。

结构锁主动锁钩被动旋转阶段，主动锁钩（含偏心套）受被动锁钩和拉簧的作用力N，f，F1，如图4所示。其中N，f的合力在Y轴上的矢量投影与对接面间的分离力T平衡，即

式中：f＝μN。此处：μ为主被动钩间的动摩擦因数。则锁钩运动时所需的驱动力矩

式中：M为锁钩运动所需的驱动力矩；h1为被动锁钩作用于主动锁钩的合力的力臂；h2为拉簧的力臂。

图4 结构锁受力Fig.4 Force of structure hook

若M＞0，则锁钩解锁时需外部动力源驱动；若M＝0，则结构锁处于阶段b）、c）的临界点S；若M＜0，则锁钩解锁时不需外部动力源驱动，而是主动带动外部动力源运动，进入主被动锁钩自主脱离阶段。

假设从0°位置运动至临界点S所需时间

式中：θS为临界点S对应的角度；ω为电机驱动结构锁运动时的角速度。从点S至完全脱钩，运动时间为T2。根据运动学原理，某一时刻t锁钩转过的角度

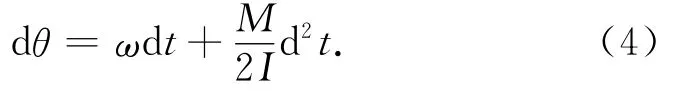
式中：I为结构锁摆动时的转动惯量。对式（4）进行积分，可得

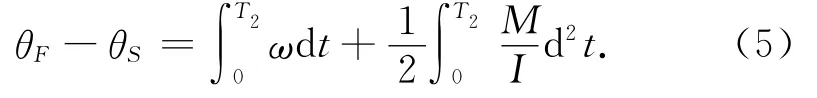
式中：θF为结构锁完全脱钩时的角度。总运动时间（脱钩时间）

结构锁实际的脱钩时间差

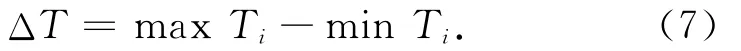
式中：i＝1～6。

由式（1）～（7）可知：结构锁的T与结构锁所受的M，ω及锁钩间的啮合长度L有关。由式（1）～（3）可知：M取决于两端面间的T，μ，F1。结构锁运动时，是由同一套驱动机构驱动，不同结构锁的ω相同，因此结构锁的脱钩时间差与L，T，μ，F1有关。

3 影响因素分析

3.1 锁钩啮合量

由于结构锁的布局和安装精度等的影响，对接时结构锁主被动锁钩间的L并不相同。根据结构设计，主动被锁钩L为9～11mm时，主被动锁钩的ΔT如图5所示。由图5可知：结构锁的ΔT与L成正比。L越大，ΔT也越大，变化率为0.49s／mm。

3.2 锁钩摩擦力

由于锁钩的加工精度、镀膜的差异以及使用时磨损程度的不同，各对结构锁钩间的摩擦因数各异，导致不同结构锁的脱钩时间也存在差异。μ为0.01～0.60时ΔT如图6所示。由图6可知：随着μ的增大，结构锁的ΔT由0s逐渐延长至1.26s。根据锁钩的材料和表面处理状态，μ为0.2～0.4时，ΔT＝0.417s。

图5 不同L的结构锁ΔTFig.5 ΔTunder various L

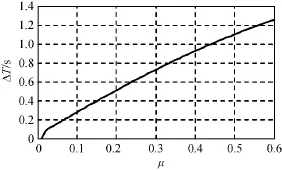
图6 不同μ的结构锁ΔTFig.6 ΔT under variousμ

3.3 拉簧力

不同F1时结构锁的ΔT如图7所示。由图可知：ΔT与F1的大小成正比。实际拉簧力的误差不超过最大值的10%，拉簧力的变化量不超过20N，ΔT＝0.02s，与摩擦因数和主被动锁钩的啮合量变化相比，拉簧力对脱钩时间差可忽略不计。

图7 不同F1的结构锁ΔTFig.7 ΔTunder various F1

3.4 端面间分离力

随着结构锁的逐渐脱钩解锁，原均匀作用于6把结构锁的端面分离力会重新分配在还未解锁的结构锁上。不同μ时，锁钩上的力为额定载荷的整数倍与结构锁脱钩时间的关系如图8所示。由图8可知：随受力锁钩数量的逐渐减少，锁钩的T将提前。提前的时间越多，越利于同步分离。

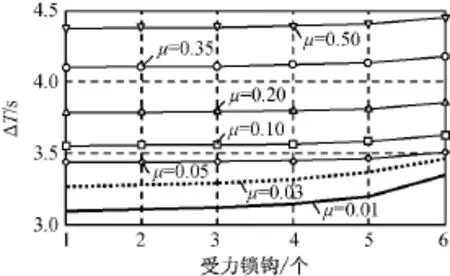
图8 不同受力锁钩数量的结构锁TFig.8 Released time under various number of stressed hooks

不同μ时，锁钩上的力为额定载荷的整数倍与结构锁ΔT的关系如图9所示。由图9可知：当μ小于0.05时，μ越小，由于锁钩受力不同导致的ΔT越大，越利于分离；当μ大于0.05时，锁钩受力不同导致的ΔT保持在稳定的水平（0.075s），不再随μ的变化而变，即端面分离力的影响可忽略不计。

图9 不同力锁钩数量的结构锁ΔTFig.9 ΔTunder various number of stressed hooks

4 结束语

本文对影响对接机构结构锁解锁同步性的因素进行了研究。建立了结构锁解锁的力学模型，研究发现：拉簧力对锁钩解锁同步性的影响可忽略不计；不同结构锁的锁钩啮合长度是影响锁钩解锁同步性的主要影响因素，应加强锁钩啮合长度的变化量控制，使锁钩的啮合长度变化量保持在较小的范围内；当负载相同时，不同结构锁摩擦因数的变化范围越大，锁钩脱钩时间变化越大，需控制摩擦因数的变化范围；考虑脱钩先后对受力的影响，当μ大于0.05时，端面分离力对同步性的影响可忽略不计。研究结果经试验验证，解决了产品研制中分离角速度过大的问题。

［1］ СЫРОМЯТНИКОВВС.空间对接机构［M］.娄汉文，曲广吉，刘济生，等（译）.北京：航空工业出版社，1992.

［2］ 郑云青，柏合民，刘 志.钢丝绳的弹性变形对锁系机构运动同步性的影响分析［J］.载人航天，2009（3）：59－63.

［3］ 肖 杰，汤树人，张 华，等.基于仿真的正交试验在对接锁系运动同步性研究中的应用［J］.宇航学报，2008，29（6）：1778－1781.

［4］ 张 华，肖余之，陈 萌，等.空间对接机构对接锁系同步性仿真研究［J］.宇航学报，2008，30（1）：310－314.

［5］ 周建平.空间交会对接技术［M］.北京：国防工业出版社，2013.

［6］ 刘志全，曹 鹏.带有偏心轮的锁钩式结构锁运动性能和力分析［J］.中国空间科学技术，2004，24（5）：43－50.