柔性太阳帆轨道－姿态－弹性振动耦合效应研究

张 瑾，翟 坤，王天舒

（清华大学 航天航空学院，北京 100084）

0 引言

太阳帆航天器是一种新型的深空探测航天器，依靠太阳光压力产生推力。太阳帆航天器自身无需携带大量的燃料用于任务，但为在微弱的光压力下获得最大推力，太阳帆有巨大的帆面及很轻的结构质量，这决定了太阳帆具大转动惯量及大挠性结构［1］。一般大挠性结构有刚度低、阻尼弱、频率低和模态密集等动力学特性，即具强非线性，这为其精确动力学模型的建立带来了困难［2］。同时在大挠性结构产生运动时，结构的振动对整体结构的动力学特性与控制的影响不可忽略［3］。

因太阳帆利用太阳光压力产生推进力，为大尺度、大挠性结构，故太阳帆是典型的姿态、轨道、振动耦合问题。目前对太阳帆的研究主要集中于太阳帆的轨道设计、姿态控制和精确受力模型三方面。在太阳帆传统的轨道设计及姿态控制中，常忽略了太阳帆的实际结构，即忽略太阳帆挠性结构的变形及振动，将太阳帆作为质点或刚体进行受力分析，并通过对姿态角的改变而调节推力的大小，从而实现对轨道的控制［4－5］。对太阳帆及类似地有挠性附件航天器来说，其弹性振动的处理方法有两种：一是将航天器结构的振动简化为影响力矩引入轨道姿态方程，二是用支撑杆的模态替代整体模态进行姿态振动耦合分析［6－9］。这两种方法都可得到与刚体模型不同的结果，说明弹性振动对太阳帆的姿态会有影响。

太阳帆在飞行过程中会不断产生变形，因帆膜刚度低，其变形较复杂，所受光压也由此变得复杂，故建立较精确的光压力模型也成为研究的目标之一［10］。通过建立精确的受力模型，可根据太阳帆实时的弹性变形得到实时受力状况［11－12］。但此种方法忽略了弹性振动对轨道、姿态的影响。文献［13］采用混合坐标法建立了柔性太阳帆动力学模型，用预应力模态完成模型降阶，建模中考虑了帆膜和支撑梁的中性面耦合变形，并通过ABAQUS／Explicit的瞬态动力学分析功能验证了该降阶模型的有效性。

对太阳帆的动力学进行了大量研究，但还没有结合了轨道、姿态、弹性振动的动力学研究。由于三者间的强烈耦合，太阳帆轨道、姿态、弹性振动的联合控制需作深入研究。本文根据文献［13］提出的柔性太阳帆动力学降阶模型，考虑天体引力及太阳光压力的作用，对柔性太阳帆在空间运行时轨道、姿态以及弹性振动的耦合效应进行了研究。

1 柔性太阳帆动力学建模

目前，太阳帆的研究多针对方形太阳帆构型，一般由支撑杆4根和三角形帆膜4块组成，在太阳帆中心可搭载小卫星等有效载荷。方形太阳帆的结构较简单，当有效帆膜面积相同时，所需支撑杆的长度更少，因此结构质量较轻，且方形太阳帆的姿态操控更简易和精确，能在行星逃逸时提供很大的转弯速度。

1.1 坐标系定义

定义地球赤道惯性坐标系O-XYZ、轨道坐标系o-xyz和太阳帆本体坐标系ob－xbybzb如图1所示。图中：Ω为升交点赤经；ω为近地点幅角；f为真近点角；i为轨道倾角。具体如下。

图1 太阳帆空间坐标系Fig.1 Coordinate systems definition for solar sail

a）O-XYZ系：坐标原点为地球质心O；OX轴指向春分点；OZ轴垂直于赤道平面；OY轴由右手法则得到。

b）o-xyz系：坐标原点为太阳帆中心在轨位置o；ox轴由地心指向航天器；oy轴垂直于轨道平面，oz轴由右手法则得到。

c）ob－xbybzb系，坐标原点为太阳帆几何中心ob；obxb，obyb轴在太阳帆平面内；obzb轴沿太阳帆法向。

初始时刻，ob－xbybzb，o-xyz系重合；点ob，o重合；太阳帆帆面指向地心。

O-XYZ，o-xyz系间的转换阵Ai2o取决于轨道所处的位置矢量r和轨道速度矢量v，有

O-XYZ系到ob－xbybzb系的转换用四元数表示为

则O-XYZ系到ob－xbybzb系的转换矩阵为

式中：

o-xyz系到ob－xbybzb系的转换矩阵可表示为

通过转换计算可得太阳帆本体系相对轨道坐标系的欧拉转角。

1.2 柔性太阳帆动力学降阶模型及方程

本文选择五点连结方形太阳帆为研究对象，如图2所示。

图2 五点连结方形太阳帆Fig.2 Five-point connected square solar sail

太阳帆的主要柔性结构包括支撑梁和帆膜。假设支撑梁为欧拉－伯努利梁，忽略其剪切变形，帆膜为薄板，跟随支撑梁产生变形。支撑梁与帆膜通过拉索在太阳帆的中心及4个端点相互连接，作为整体建模。太阳帆上任一点相对惯性系O点的矢径为

式中：RO为点ob相对O-XYZ系原点O的矢径；rf为未变形时该点相对点ob的矢径；uf为该点的变形矢量。仅考虑柔性结构的横向变形及由此引起的中性面耦合变形，uf在ob－xbybzb系中的表达式为

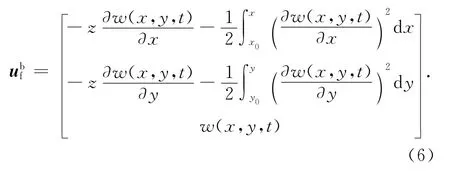
式中：w（x，y，t）为中性面的横向变形；（x0，y0）为中性面上不发生变形的点，即为点ob。

对横向变形w进行模态离散可得模态坐标表达式

式中：Φ为通过预应力模型分析得到的模态振型；q为模态坐标。数值仿真时仅保留前3阶模态完成模型降阶。用ABAQUS／Standard预应力分析，所得模型的前三阶非刚体频率及振型如图3所示。

图3 柔性太阳帆前三阶非刚体频率及振型Fig.3 Frst three non-rigid-body frequencies and mode shapes of solar sail

忽略各种天体摄动力和耗散阻力，仅考虑天体引力和太阳光压力，根据虚功率原理，有

式中：ps为作用在帆面上的太阳光压；pg为天体引力；Kf为柔性结构模态刚度矩阵；，分别为太阳帆上任一点的速度变分和模态速度变分；dm，dA分别为该点的质量与面积。

将R对时间的一、二次导代入式（8）可得柔性太阳帆轨道－姿态－振动耦合方程

式中：mtot为太阳帆的总质量；Sf为太阳帆与弹性振动耦合后的静矩；Jf为太阳帆与弹性振动耦合后的转动惯量；ω为本体系相对惯性系的角速度矢量；Ct为平动与弹性振动耦合矩阵；Cr为转动与弹性振动耦合矩阵；ΦNL为变形矢量uf相对模态坐标q求导的导数矩阵；Qft，Qfr，Qff分别为平动、转动、振动耦合产生的力及力矩；Ft，Fr，Ff分别为太阳光压力产生的力及力矩；Fgt，Fgr，Fgf分别为天体引力产生的力及力矩；（·），（··）分别为惯性系中对时间的一次导和二次导，（′），（″）分别为为本体坐标系中对时间的一次导和二次导。

用四元数Λ＝［Λ0Λ1Λ2Λ3］T描述太阳帆的姿态，则式（9）在本体系中可写成

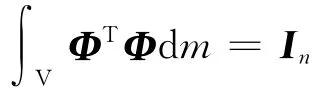
根据四元数导数与运动角速度间的关系

可将式（10）转换成状态空间方程

综上，对式（16）可直接进行数值求解，本文采用MATLAB中的龙格库塔四－五阶积分函数ode45进行数值求解。计算结果可根据各坐标系间的转换矩阵进行换算。

1.3 太阳帆模型参数

如图2所示，太阳帆包含支撑梁4根和等腰直角三角形帆膜4个，每个帆膜通过绳索3根与支撑梁连接，太阳帆法线方向有控制杆。在太阳帆支撑梁的4个端点有质量0.58kg的姿控小帆，在太阳帆中心有质量54.84kg的盒舱，在控制杆末端有质量228kg的有效负载。太阳帆的结构参数见表1。

因控制杆末端存在较大质量的有效负载，故太阳帆质心与中心（本体系原点）不重合，太阳帆质心在本体系中可表示为

太阳帆受到的引力梯度力矩

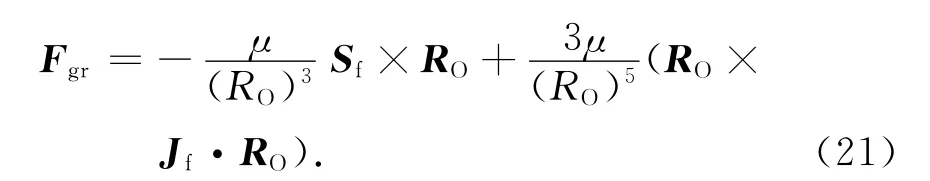
式中：μ为地球引力常数。可看出：由于太阳帆的偏心质量，太阳帆所受的引力梯度力矩有所增大，其转动角位移也会明显增大。同时，由式（9）也可发现：由于轨道与姿态的耦合性，由光压力引起的轨道偏差亦会对太阳帆的姿态产生影响。

2 轨道－姿态－弹性振动耦合效应

文献［14］研究了刚体帆在大偏心率地球椭圆轨道上太阳帆帆面对地指向及对日指向的姿态控制过程。由于地心轨道的引力较大，并且大偏心率椭圆轨道的引力及重力梯度力矩变化较大，更有利于检验太阳帆轨道－姿态－振动耦合效应，因此本文对柔性太阳帆在大偏心率椭圆轨道进行动力学分析，检验其轨道－姿态－振动耦合效应。

不考虑对太阳帆的控制，令太阳帆只依靠天体引力运行，地心椭圆轨道相应轨道要素为a＝46 428km，e＝0.819 6，i＝12°，f0＝0°；在地球轨道上的太阳光压力大小为ps＝9.12×10－6Pa。假设太阳帆初始时刻本体坐标系与轨道坐标系重合，即帆面指向地心，太阳帆相对地球惯性坐标系初始角速度为0。

由于太阳帆耦合动力学方程中是对其轨道、姿态及模态坐标同时进行求解，而三者的数值量级存在很大差异，为保证姿态与模态坐标的求解精度，在方程求解时积分的绝对误差与相对误差分别取为10－12，10－10。MATLAB中ode45积分函数是变步长积分函数，为节约输出内存并完整体现太阳帆的振动特性，根据太阳帆的自然频率可选定输出步长为3s。

表1 太阳帆结构参数Tab.1 Structural parameters of solar sail

2.1 刚性太阳帆动力学

先不考虑太阳帆的柔性，则式（9）可退化为轨道、姿态耦合方程

在地心椭圆轨道进行2个轨道周期的数值仿真。仿真结果如图4～12所示。

太阳帆运行轨道在地球赤道惯性系XOY平面上的投影如图4所示。由图可知：在太阳光压力的作用下，太阳帆的轨道出现了偏差，轨道半长轴最大偏移量369.206km。

图4 太阳帆XY平面内轨道Fig.4 Representation of orbit inXYplane for solar sail

对一般航天器，在无光压力及其他摄动力作用时，航天器仅受轨道平面法线方向上的重力梯度力矩作用，将只存在轨道平面法线方向上的角速度和角位移。由于太阳帆在大偏心率的椭圆轨道上运动，引力梯度力矩随轨道半径变化出现较大变化，轨道角速度也发生明显变化，且由于太阳帆质心与中心不重合，会存在较大引力梯度力矩，太阳帆相对轨道坐标系y向会出现较大的角位移。同时由于太阳帆动力学方程的耦合性，在太阳光压力作用下，太阳帆相对轨道坐标系x、z向也出现了较大角位移，如图5～7所示。由图可知：太阳帆相对x向欧拉角在±50°间振荡。相对y、z向也存在大范围的变化，由图8～10可知：太阳帆在轨道坐标系三个方向的角速度的量级相同，且呈持续振荡，其最大振幅均为0.1（°）／s。

由上述刚性太阳帆在大偏心率地心椭圆轨道上的动力学分析可知：太阳光压力引起了太阳帆相对原轨道的偏差。由于太阳帆质心与中心的不重合，在太阳光压力的作用下，太阳帆会在3个方向上均出现大幅的角位移变化。

图5 太阳帆相对轨道坐标系x轴角位移Fig.5 Representation of angular displacement atx-axis for solar sail

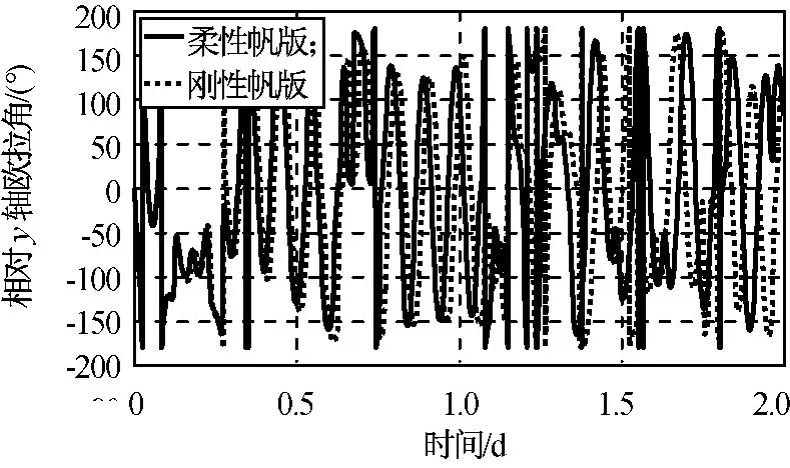
图6 太阳帆相对轨道坐标系y轴角位移Fig.6 Representation of angular displacement aty-axis for solar sail

图7 太阳帆相对轨道坐标系z轴角位移Fig.7 Representation of angular displacement atz-axis for solar sail

2.2 柔性太阳帆动力学

考虑太阳帆的柔性，动力学方程为式（9），对柔性太阳帆在地心椭圆轨道上进行2个轨道周期的动力学仿真。

太阳帆轨道在地球赤道惯性系XOY平面的投影如图4所示。在太阳光压力以及自身弹性振动的作用下，太阳帆运行轨道产生了偏差，其轨道半长轴的最大偏移量369.216km，与刚性太阳帆的结果近似。可见，太阳光压力是太阳帆轨道产生偏差的主要原因，太阳帆柔性结构振动对其轨道影响很小。

图8 太阳帆相对轨道坐标系x轴角速度Fig.8 Representation of angular velocity atx-axis for solar sail

图9 太阳帆相对轨道坐标系y轴角速度Fig.9 Representation of angular velocity aty-axis for solar sail

图10 太阳帆相对轨道坐标系z轴角速度Fig.10 Representation of angular velocity atz-axis for solar sail

与刚性太阳帆相同，柔性太阳帆相对轨道坐标系x、y、z向均出现了较大的角位移变化，太阳帆相对x向欧拉角在±70°间振荡，相对y、z向欧拉角变化范围更大。与刚性太阳帆相比，柔性太阳帆虽在三个方向上同样存在大幅转角，但在结构振动的作用下，其角位移随着时间的增长逐渐出现差异，并随着时间的增长偏差逐渐增大，说明太阳帆的柔性对其姿态的影响具有时间的累积效应，且这种影响不可忽视。

由太阳帆相对轨道坐标系三个方向的角速度可知：与刚性太阳帆相似，柔性太阳帆三个方向的角速度也有相同量级，其最大振幅均为0.1（°）／s。同样的，柔性太阳帆与刚性太阳帆的角速度变化曲线类似，但是在太阳帆柔性的影响下，太阳帆角速度曲线逐渐出现偏差，并随着时间的增长偏差逐渐增大。

柔性太阳帆端点1处的横向变形及伸长变形分别如图11～12所示。太阳帆端点1处最大横向变形0.65m，最大伸长变形0.002 5m。由局部放大图可知：在端点变形的增大与减小过程中，太阳帆的柔性结构仍存在小幅高频的弹性振动，其振动周期约38s。

图11 太阳帆端点1处横向变形Fig.11 Deflection deformation at tip 1for solar sail

由柔性太阳帆在大偏心率地心椭圆轨道上的动力学分析可知：太阳光压力引起了太阳帆轨道的偏差，以及柔性结构的弹性变形及振动。由于大偏心率椭圆轨道上引力梯度力矩的较大变化，以及太阳帆质心与中心的不重合，在太阳光压力的作用下太阳帆会产生较大幅度的转动角位移和角速度，进而引起太阳帆柔性结构较大幅度的弹性变形及振动。同时，太阳帆柔性结构的振动也会导致其姿态产生与刚性太阳帆不同的姿态变化，而这种影响是一个长时间的积累效应，且其影响不可忽视。

图12 太阳帆端点1处伸长变形Fig.12 Stretching deformation at tip 1for solar sail

3 结束语

本文建立了柔性太阳帆轨道－姿态－弹性振动耦合的动力学降阶模型，研究了太阳帆轨道、姿态和结构弹性振动的耦合效应。研究表明：太阳光压力是引起太阳帆轨道产生偏差的主要原因，同时会引起太阳帆柔性结构的弹性变形及振动；当太阳帆质心与中心不重合时，较大的引力梯度力矩以及轨道和姿态的耦合特性会引起太阳帆姿态的大幅变化；太阳帆柔性结构的振动会随时间的增加引起姿态的偏差，这种随时间积累的偏差在长期的深空探测任务中非常重要。同时，通过分析也可发现：由于在地球轨道上太阳帆所受的引力较大，会对太阳帆姿态和弹性变形产生较大的影响，因此，为更好地发挥太阳帆的推力优势，应将太阳帆用于深空探测任务中。为克服太阳帆偏心对其姿态的影响，可通过适当的姿态控制方案保持其姿态的稳定，进而实现轨道的稳定。柔性太阳帆在空间飞行是一个轨道、姿态、弹性振动强烈耦合的复杂问题，其耦合效应的研究对其长期深空探测任务的完成具有重要意义。

［1］ 王伟志.太阳帆技术综述［J］.航天返回与遥感，2007（2）：1-4.

［2］ 司洪伟，李东旭，陈卫东.大挠性航天桁架结构动力学及其主动控制研究进展［J］.力学进展，2008，38（2）：167-176.

［3］ 刘 军，韩 潮.挠性航天器大角度机动的振动抑制控制［J］.系统仿真学报，2008，20（7）：1880-1883.

［4］ WIE B.Thrust vector control analysis and design for solar-sail spacecraft［J］.Journal of Spacecraft and Rockets，2007，44（3）：545-557.

［5］ GONG Seng－ping，LI Jun-feng，BAOYIN He-xi.Passive stability design for the solar sail on displaced orbits［J］.Journal of Spacecraft and Rockets，2007，44（5）：1071-1079.

［6］ 李争学，王本利，马兴瑞.带挠性附件航天器的鲁棒姿态跟踪控制［J］.宇航学报，2009，30（3）：974-981.

［7］ LIU Ying－ying，ZHOU Jun.Dynamics model and simulation for flexible satellite with orbit control force［C］／／Proceedings of the 2010 3rd IEEE International Conference on Computer Science and Information Technology （ICCSIT 2010）.Piscataway：IEEE Press，2010，9：227-230.

［8］ SMITH S W，SONG H B.Flexible models for solar sail control［C］／／46th AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics ＆ Materials Conference.Austin：American Inst Aeronautics and Astronautics Inc，2005，1：11-40.

［9］ LIU Jia-fu，RONG Si-yuan，LI Jian-guo，et al.Attitude dynamics modeling and control of large flexible solar sail spacecraft［C］／／ 2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics （ISSCAA 2010）.Piscataway：IEEE Press，2010：243-247.

［10］ WANG C G，MAO L N，DU X W，et al.Influence parameter analysis and wrinkling control of space membrane structures［J］.Mechanics of advanced materials and structures，2010，17（1）：49-59.

［11］ SAKAMOTO H，MIYAZAKI Y，PARKT K C.Finite element modeling of sail deformation under solar radiation pressure［J］.Journal of Spacecraft and Rockets，2007，44（3）：514-521.

［12］ DAVID M，THOMAS T.Solar sail propulsion modeling［C］／／ 48th AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics，and Materials Conference.Reston： American Institute of Aeronautics and Astronautics Inc，2007，2：1452-1468.

［13］ LI Qing，WANG Tian-shu，MA Xing-rui，Reduced model of flexible sail-boom interaction for solar sail dynamics［C］／／60th International Astronautical Congress 2009（IAC 2009）.Paris：International Astro-nautical Federation，2009，6：5045-5055.

［14］ WIE B，Solar sail attitude control and dynamics（part 1）［J］.Journal of Guidance，Control，and Dynamics，2004.27（4）：526-535.