PU／P（MMA－EA）互穿网络热分解研究

刘晓宁，左海丽，朱 勇，黄洪勇，张 兵

（1.中国人民解放军海军驻上海地区航天系统军事代表室，上海 201109；2.上海航天动力技术研究所，浙江 湖州 313000）

0 引言

近年来利用IPN技术改性聚氨酯以提高高分子材料性能成为研究热点。互穿网络聚合物（IPN）是两种或两种以上交联聚合物相互贯穿而形成的交织网络聚合物，作为聚合物共混与复合的重要物质，可充分发挥各网络的优势，目前已用于提高推进剂黏合剂体系性能［1］。文献［2］在原有丁羟推进剂黏合剂体系中添加甲基丙烯酸B酯作为塑料相，降低了预聚物黏度，改善了加工工艺性能并提高了力学性能。文献［3］通过复合固化方法制备了一种非均相的海岛状互穿网络结构的聚合物，其中一个体系是由SM6204丙烯酸酯与BP／BE复合光引发剂组成的UV固化体系组成，另一个体系是由HTPB与IPDI组成的热固化体系。文献［1］分析了IPN的技术特点，综述了IPN在固体推进剂黏合剂固化体系中提高固体推进剂力学性能、改善加工工艺性能和增强抗蠕变性能等方面的应用前景，并概述了IPN在固体推进剂衬层和包覆层中的应用［4］。文献［5］将互穿网络作为调整NEPE推进剂黏合剂网络结构的主要措施之一。目前，已对互穿聚合物网络在推进剂中的应用进行了研究，但对互穿聚合物网热分解动力学的研究相对较少，本文采用非等温法研究了聚氨酯和聚丙烯酸酯形成互穿网络聚合物的各阶段的热分解，以及相关动力学参数和机理函数。

1 实验

1.1 实验材料

端羟基聚丁二烯（HTPB），黎明化工研究院；异佛尔酮二异氰酸酯（IPDI），黎明化工研究院；甲基丙烯酸甲酯（MMA），化学纯，上海凌风化学试剂有限公司；丙烯酸乙酯（EA），化学纯，上海凌风化学试剂有限公司。

1.2 PU／P（MMA－EA）制备

将计量好的HTPB，IPDI与按一定比例称取的MMA，EA置于烧杯中混合均匀，并加入催化剂和引发剂，室温下充分搅拌后减压脱泡，浇注到喷涂有聚四氟乙烯的模具中，60℃固化7d后脱模可得PU／P（MMA－EA）胶片。

1.3 热重／微熵热重（TG／DTG）分析

用TG／DTA6200型 TGA仪进行 TG／DTG分析。样品是PU／P（MMA－EA）配比分别为100／0，90／10，70／30，PU／P（MMA－EA）质量（0.8±0.01）mg，测试气氛为氮气，氮气流速为30.0mL／min，升温速率分别为5，10，15，20K／min，温度为50～800℃。

2 结果与讨论

2.1 PU／P（MMA－EA）热分解过程

对不同升温速率和不同PU／P（MMA－EA）配比的互穿体系进行TG测试。其中PU／P（MMAEA）配比为90／10的氮气气氛中TG，DTG曲线如图1所示。由图1可知：随着升温速率的增加，互穿网络结构的失重峰向高温推移（见表1）。在热分析过程中，随着温度的升高，试样的分子链运动逐渐加剧，进而产生断链，当升温速率提高时，分子链运动的松弛时间跟不上实验观察时间，表现为失重峰向高温推移。因分子链运动及分解的活化能间接表达了分子链松弛与温度的关系，故用DTG热分析法可分析分解动力学。

图1 不同升温速率下PU／P（MMA－EA）的TG／DTG曲线Fig.1 TG／DTG curves of thermal decomposition of PU／P（MMA－EA）at different heating rates

另由图1可知：PU，PU／P（MMA－EA）的热分解分为两个阶段，预示整个热解过程主要是由两个阶段组成。其中：第一阶段主要为聚氨酯网络中硬段的氨基甲酸酯基团的分解，质量损失约29%，与体系设计的硬段含量（30%）基本一致；第二阶段为软段长链高分子裂解和聚烯烃网络的分解，质量损失约69%。

a）Kissinger法求PU／P（MMA－EA）反应活化能

不同升温速率下DTG曲线的三个Gaussian峰的峰温数据见表1，用Kissinger法求PU／P（MMAEA）反应活化能

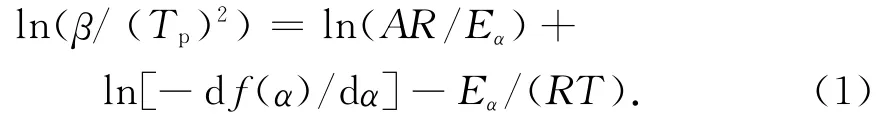
式中：β为升温速率；TP为DTG曲线上的峰温；A为指前因子，R为气体普适常数；Eα为活化能；α为转化率（反应深度）；f（α）为反应机理函数的微分形式［6］。

将ln（β／（TP）2）对1／T作图，由直线的斜率可求出PU／P（MMA－EA）热分解两个阶段的反应活化能，由截距可得A，结果见表2。表中：E为聚氨酯硬段区氨基甲酸酯基分解活化能。

表1 图1中PU／P（MMA－EA）＝90／10分解出各峰的特征量Tab.1 Eigenvalues of each separated peak of PU／P（MMA－EA）＝90／10in Fig.1

表2 Kissinger，Ozawa法计算PU／P（MMA－EA）各阶段动力学参数Tab.2 Kinetic parameters of each stage of PU／P（MMA－EA）obtained by Kissinger and Ozawa methods

由表2可知：随着丙烯酸树脂含量增加，E略有降 低，由 PU／P（MMA－EA）配 比 为 100／0 的114kJ／mol降低至配比为70／30的88kJ／mol，这可能是由于丙烯酸体系的引入，带来1，3－二丁烯和4－乙烯环己烯等低分子量碳氢化合物的挥发所致［6］。第二分解阶段则随着丙烯酸树脂含量的增加，体系的活化能有较大幅的增大，这是因为互穿网络基体之间相互作用使键断裂能增大。本文三种配比的PU／P（MMA－EA）体系中，90／10的互穿程度较好，表现为活化能也较高，由无互穿体系的153kJ／mol增至223kJ／mol。可见，互穿体系的引入有利于提高体系的热稳定性。

b）Ozawa法求PU／P（MMA－EA）反应活化能

Ozawa法避开了反应机理来求取活化能，常用于检验其他方法求出的活化能值，有

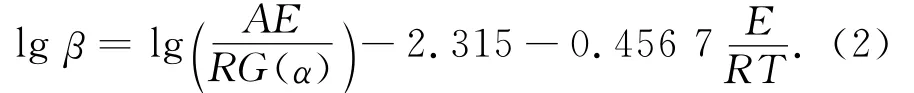
式中：G（α）为反应机理函数［6］。

假设在不同升温速率的峰温处TG曲线有相近的转化率（反应深度）。根据表1特征量，用Ozawa法，根据式（2）将lnβ对1／T作图，由直线斜率可求出活化能，结果见表2。由表2可知：用Ozawa法求得的活化能分别为158，223，219kJ／mol，与 Kissinger法的结果基本一致。

为了解整个PU／P（MMA－EA）分解过程中活化能随反应深度的变化，用Ozawa法求解整个过程的活化能。α为0.1～1.0时lnβ－1／T曲线如图2所示，由直线斜率求得的不同α时活化能如图4所示。由图3可知：PU／P（MMA－EA）的活化能变化也存在两个阶段，第一阶段α＝0.10～0.30，平均活化能111kJ／mol，第二阶段α＝0.60～0.95，平均活化能238kJ／mol。由此可见，PU／P（MMA－EA）的确存在两个阶段的热分解，其活化能值与用特征量求解的结果基本一致。

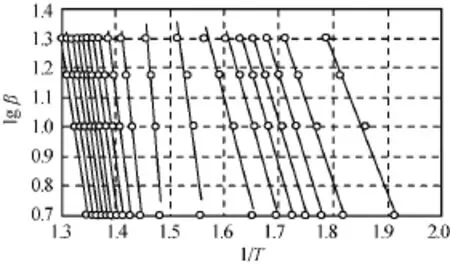
图2 α为0.1～1.0时PU／P（MMA－EA）lgβ－1／T曲线Fig.2 lgβ－1／Tcurves of PU／P（MMA－EA）atα＝0.1～1.0

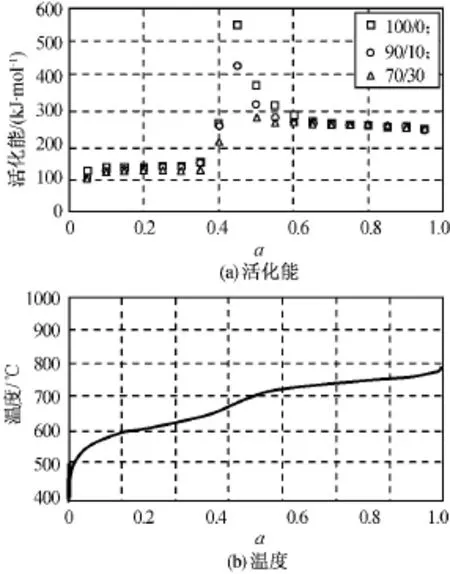
图3 不同α时PU／P（MMA－EA）活化能和温度Fig.3 Activation energy and reaction temperature of PU／P（MMA－EA）with differentα

2.2 PU／P（MMA－EA）热分解最概然机理函数推断

在非等温动力学分析中，最概然机理函数的推断有多种方法。本文将

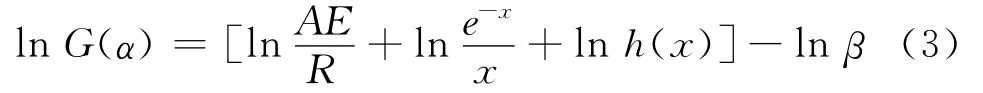
用于估算G（α）［7－8］。将相同温度下不同加热速率对应的失重率α代入表3中反应机理对应的G（α）的数学表达式中，由lnG（α）对lnβ的线性关系可获得斜率和相关系数，反应机理为直线的斜率，最接近－1，且相关系数更高者，以PU／P（MMA－EA）配比90／10第一阶段分解为例，计算结果见表3，PU／P（MMA－EA）配比100／0，70／30的结果见表4。

表3 与反应机理对应G（α），f（α）数学表达式及计算结果Tab.3 Algebraic expressions of functions G（α），f（α）corresponding mechanism and calculation results

表4 不同PU／P（MMA－EA）配比各阶段与反应机理对应G（α）数学表达式及计算结果Tab.4 Algebraic expressions of functions G（α）with different PU／P（MMA－EA）at different stage corresponding mechanism and calculation results

由表3可知：6＃动力学函数斜率最接近－1，且相关系数较好，由此可判定PU／P（MMA－EA）第一阶段的热分解反应遵循动力学函数为6＃，其积分形式G（α）＝（1－α）－3－1，微分形式f（α）＝1／3（1－α）4。由表4可知：PU／P（MMA－EA）配比分别为100／0，90／10，70／30第一阶段热分解所遵循的动力学函数号分别为13＃，6＃，5＃，第二阶段热分解所遵循的动力学函数号分别为30＃，30＃，11＃。

3 结论

根据PU／P（MMA－EA）热分解DTG曲线的特点，其热分解过程可分为两个阶段，用Kissinger法求得PU／P（MMA－EA）配比为100／0，90／10，70／30三种体系两个阶段的活化能。从第二阶段的热分解活化能可发现在PU体系中引入互穿体系后，活化能有所增加，由无互穿体系的153kJ／mol增至PU／P（MMA－EA）配比90／10的223kJ／mol，可见该配比的互穿程度较好，利于提高体系的热稳定性。用Ozawa法求得的活化能与Kissinger法基本一致。用最概然机理函数推断出每种配方各阶段所遵循的函数，其中 PU／P（MMA－EA）配比为90／10的第一、二阶段遵循的动力学函数的积分形式分别为G（α）＝（1－α）－3－1，G（α）＝（（1－α）－1／3－1）2。

［1］ 高建宾，张宏元，陶永杰.互穿聚合物网络技术在固体推进剂中的应用前景［J］.化学推进剂与高分子材料，2003，1（4）：11－14.

［2］ 张 磊，范夕萍，谭惠民.互穿聚合物网络技术对丁羟推进剂粘合剂体系性能的改善［J］.精细化工，2006，23（10）：1019－1022.

［3］ 杨时敏.固体火箭发动机复合固化衬层的研制［D］.长沙：国防科学技术大学，2008.

［4］ PARTHIBAN S，RAGHUNANADAN B N，JIAN S R.Interpenetrating polymer networks as binders for solid composite propellants［J］.Defence Science Journal，1992，42（3）：147－156.

［5］ 刘晶如，宋雪晶，杨 寅.NEPE推进剂粘合剂网络结构调节研究［J］.固体火箭技术，2010，33（1）：72－76.

［6］ 刘子如.含能材料热分析［M］.北京：国防工业出版社，2008.

［7］ LI Z J，SHEN X Q，FENG X，et al.Non－isothermal kinetics studies on the thermal decomposition of zinc hydroxide carbonate［J］.Thermochimica Acta，2005，438（1／2）：102－106.

［8］ VLAEV L，NEDELCHEV N，GYUROVA K，et al.A comparative study of non－isothermal kinetics of decomposition of calcium oxalate monohydrate［J］.Journal of Analytical and Applied Pyrolysis，2008，81（2）：253－262.