结合第一性原理和热力学计算对HfO2晶体本征点缺陷的预测
2015-12-29刘凤明刘廷禹李海心
刘凤明 刘廷禹 刘 检 李海心
(上海理工大学理学院,上海200093)
结合第一性原理和热力学计算对HfO2晶体本征点缺陷的预测
刘凤明 刘廷禹*刘 检 李海心
(上海理工大学理学院,上海200093)
基于第一性原理和热动力学方法模拟计算得到了不同温度和氧分压下HfO2晶体本征点缺陷的形成能,并讨论了各种点缺陷的形成能随费米能级变化的规律.结果表明:当费米能级在价带顶附近时,随着温度和氧分压的变化,出现了不同的最稳定点缺陷(O0i、V2+O3和Hfi4+).当费米能级大于3.40 eV时,主要点缺陷是带-4价的Hf空位.该晶体除Hf空位在价带顶附近出现了奇数价态,其它的点缺陷都只显现偶数价态,这表明该晶体的点缺陷具有典型的negative-U特性.本文还计算得到了该晶体可能存在的最稳定点缺陷在温度、氧分压和费米能级三维空间的分布,这为分析该晶体在不同条件下可能出现的点缺陷类型提供清晰的图像,为调控晶体点缺陷的形成提供参考.
密度泛函理论;点缺陷;热力学;二氧化铪晶体
1 引言
二氧化铪(HfO2)是一种重要的宽禁带过渡金属氧化物,因为它具有高硬度、高熔点、高化学稳定性、高中子吸收横截面、完美的介电性能和在可见光及紫外区具有良好的透明特性等优良物理化学性能,HfO2作为绝缘体在光学涂层及电子和光学设备等领域得到广泛的应用.1,2因此该晶体受到广泛的关注.
©Editorial office ofActa Physico-Chimica Sinica
当二氧化硅(SiO2)作为栅极绝缘层材料时,随着其物理厚度的减小,栅极漏电可能性急剧增加.研究者正在努力寻找可以替代SiO2的材料,高介电常数的金属氧化物介质进入大家的视野,并且最近成为热点.3-16在所有的金属氧化物半导体中,HfO2不管从氧化物的高介电特性及较宽的带隙,还是从生产工艺上的优势(在Si上具有优良的化学稳定性和热稳定性,以保证其在金属氧化物半导体场效应管的生产工艺过程中不与Si发生反应,且相互扩散要小,可以防止形成厚的SiOx界面层和硅化物层),是最有可能成为晶体管栅极绝缘层材料,而成为替代SiO2首选材料.17然而,二氧化铪薄膜作为栅极绝缘层受到各类晶体缺陷的影响.比如,退火过程产生的填隙氧等带电缺陷会产生很强的电场而引起能带弯曲,它们对介电损耗的贡献及在电场中的扩散影响了其作为栅极绝缘层的性能.17-23因此,对HfO2本征缺陷的研究对改善其电学性能十分重要.
随着计算机技术和计算理论的发展,计算机模拟技术在各研究领域已经得到广泛的应用.24国内外对利用计算机模拟技术对HfO2本征缺陷开展了大量研究.Robertson等25,26的研究结果表明在HfO2晶体中氧空位是主要的电子陷阱.Foster等27对HfO2的本征点缺陷形成能和能级进行了大量的研究表明氧填隙和带正电的氧空位都是主要的电子陷阱.Shen等28的研究证明了在HfO2中氧空位和氧填隙具有negative-U特性.Kang等29的研究提出经过淬火后出现带正电的缺陷是由于在复杂环境条件下氧空位和氢填隙结合为“Vo-H”缺陷簇.Zheng等30研究了富氧和缺氧条件下的本征缺陷的基本性质.
然而,所有以上这些对该材料本征缺陷的研究都只局限于富氧和缺氧两种极端条件下的讨论,而没有考虑一般的条件下(不同的环境温度和氧偏压)对缺陷形成能(DFE)的影响,从而影响了对该晶体中本征点缺陷一般规律的认识.因此,本文将通过研究该晶体本征点缺陷的形成能与环境温度、氧分压和费米能级的具体关系,得到外部条件对缺陷稳定性的影响,为调控该晶体点缺陷提供理论指导.
2 计算方法
2.1 电子结构计算
本文使用VASP软件包对HfO2晶体进行模拟计算.交换关联泛函使用广义梯度近似(GGA-PBE),31-34Hf的价电子为5p65d26s2,O的价电子为2s22p4,平面波截断动能为500 eV,本文采用Monkhorst-Pack k点取样方法对布里渊区进行积分,k网格点为6×6× 6.以上参数都经过收敛测试确定.HfO2在室温下主要以单斜结构相存在,所以本文将对该晶体的单斜结构进行研究,在单斜结构HfO2晶体中存在两种不同的氧位置,分别记为O3和O4,O3代表氧最近邻有3个金属离子,O4代表氧最近邻有4个金属离子,而Hf离子最近邻有7个氧原子.本文以12个原子的原胞为基础建立2×2×2超晶胞(含96个原子)作为计算模型.单斜相HfO2(m-HfO2)晶体原胞如图1所示.
2.2 缺陷形成能的计算
点缺陷的吉布斯自由能是关于缺陷种类α,带电态q,氧分压p和温度T的函数,具体表达式如下:

上式中,Etotal(α,q)代表带电量为q的α缺陷的超晶胞经弛豫后的总能,Etotal(perfect)则是完整晶体的超晶胞经弛豫后的总能,它们利用VASP计算获得.nα值是指从超晶胞中移除或者添加α原子的数量.比如nα=nO=-1意味着超晶胞增加了一个氧填隙,nα=nHf=1则是超晶胞中有一个Hf空位.μα(T,p)是对应原子随温度和氧分压变化的化学势,它通过VASP和热力学计算获得,后面有详细的描述.EVBM是价带顶的能级,EF是指电子相对价带顶的费米能级,费米能级随缺陷浓度和样品中杂质的浓度以及环境条件而变化.ΔV为含缺陷的超晶胞与完整的超晶胞间的平均静电势之差,35振动熵对缺陷形成能影响较小,因此本文未予考虑.
2.3 热力学部分
氧的化学势关于温度与氧分压的函数,具体关系如下36,37

图1 m-HfO2的晶胞结构Fig.1 Structure of m-HfO2crystal cell

3 结果与讨论
3.1 热力学跃迁能级
热力学跃迁能级指同一种点缺陷不同带电态q1和q2具有相同的缺陷形成能时,两者相对应的费米能级,即E(defect q1/q2),通过方程(1)计算得到,各种点缺陷的热力学跃迁能级在禁带中的分布如图2所示.图中VO3,VO4和VHf代表O3,O4和Hf的空位,Oi和Hfi分别代表O和Hf的填隙.从图2中可以发现,所有的施主缺陷(VO3,VO4和Hfi的各种价态)都有深的热力学跃迁能级,而受主缺陷(Oi和VHf的各种价态)中除了E(Oi,-1/0)外都为浅的热力学跃迁能级,这些浅的热力学跃迁能级意味着缺陷的价态转换比较容易发生.分析氧空位的热力学跃迁能级发现,它的转换不是正常的顺序,而是0/+1的跃迁能级在+1/+2之下,即费米能级在禁带区域内的变化,+1的氧空位缺陷形成能比0或者+2价的氧空位的缺陷形成能都高,因此没有一个费米能级的位置使得带+1价的氧空位是热力学稳定的,这就是典型的negative-U特性,跟Shen等28的研究一致.从图2中可以看出,除了Hf空位热力学跃迁能级是正常排序,其他所有的本征点缺陷都表现类似的特性,即negative-U特性.25-28

图2 主要缺陷的热力学跃迁能级E(defect q1/q2)的计算结果Fig.2 Calculated thermodynamics defect transition levels E(defect q1/q2)for the major defects
3.2 缺陷形成能和结果讨论
结合方程(1)和方程(2),可以知道各类缺陷形成能是关于温度、氧分压和费米能级的三元函数.为了全面研究缺陷形成能与它们的关系,本文在整个三维空间计算了缺陷形成能随温度、氧分压和费米能级变化的分布,图3中的曲面是两种最稳定的点缺陷转化的分界面(即在这个分界面上两种点缺陷的形成能相等).该图很好地表达了晶体中主要点缺陷在温度、氧分压和费米能级三维空间的分布,清晰地展现了不同条件下的主要点缺陷的类型.
从图3区域1发现:当费米能级处于1.18-3.40 eV之间,在曲面3下方是最稳定的缺陷;而从费米能级处于3.40-5.90 eV之间时,在任何温度和氧分压下都是最稳定的点缺陷类型.在区域2(在曲面2与曲面3之间)中发现,当费米能级处于0.41到3.40 eV之间时,最稳定的点缺陷为带负二价的氧填隙和零价的氧填隙区域3中(在曲面1与曲面2之间),费米能级从0到2.95 eV变化时,是最稳定的点缺陷.在图中区域4,即高温、低氧分压和较小费米能级环境下,是主要的点缺陷.

图3 随温度、费米能级和氧分压变化的最稳定点缺陷分布的三维图Fig.3 Three-dimensional scheme of the most stable defects distribution as functions of temperature, Fermi energy,and oxygen partial pressure
材料的实际费米能级会随着杂质或者掺杂浓度的不同而改变,另外还受温度与氧分压的影响,因此本文有必要讨论费米能级在整个禁带里变化对缺陷形成能的影响.为了更详细的描述温度、氧分压和费米能级三者与缺陷形成能的关系,本文作了进一步的分类讨论.首先,本文分别选取了不同温度压强下,各种缺陷形成能与费米能级变化的关系,如图4所示.从图中可以看出点缺陷的形成能与温度和费米能级的改变有很大的关系.图4(a3,b3,c3)为在还原条件(lg(pO2)=-10)下,没有掺杂的HfO2中VHf、Hfi、VO、Oi、HfO(Hf替换O)和OHf的缺陷形成能随费米能级变化的关系.在常温和低氧分压下,费米能级从0 eV上升到5.90 eV的过程中(图4a3),最稳定的点缺陷依次是和而当费米能级在1 eV附近时,和的缺陷形成能比较接近,说明在这种条件下,这些缺陷都有可能同时存在.随着费米能级的增加,Hf填隙电子态转换是从+4到+2再到0,而不会出现奇数价态,偶数的电子态缺陷是最容易形成而最稳定.在T=300 K和pO2=10-10Pa条件下,费米能级从1.14到5.90 eV的变化区间受主型点缺陷一直是最稳定.然而,在相同的温度与氧分压条件下,当EF=0-0.53 eV和EF= 0.53-1.14 eV时,最稳定点缺陷分别为和在HfO2中,当费米能级靠近导带底时,的缺陷形成能是最低的,表明在该条件下是HfO2中最稳定的本征点缺陷.
从图4中还可以看出,不管温度、氧分压和费米能级如何变化,的缺陷形成能总比的缺陷形成能低0.63 eV(跟Foster等27的研究接近).而的缺陷形成能总比的缺陷形成能高0.13 eV.本文中,氧空位一直是偶数价态,即与图2结论和实验中证实HfO2中氧空位具有negative-U特性一致.28

图4 缺陷形成能(DFE)在不同氧分压、温度条件下关于费米能级的函数Fig.4 Calculated defect formation energy(DFE)of point defects as function of Fermi level at different oxygen partial pressures and temperatures
在10-5Pa氧分压下,当费米能级从0到5.90 eV逐渐变化时,在温度分别为300、900和1800 K时,对应的最稳定点缺陷分别为(图4a2),(图4b2)(与Zheng中提出的一般情况下的最稳定缺陷形成能吻合)和(图4c2).然而,当温度固定为900 K,费米能级从0到5.90 eV逐渐变化时,在不同的氧分压103、10-5和10-10Pa下,对应最稳定点缺陷排序却分别为(图4b1),(图4b2),(图4b3).当氧分压和温度都不同时,最稳定点缺陷随费米能级的变化所对应的点缺陷又变为(图4a1,300 K和103Pa),(图4b2,900 K和10-5Pa),(图4c3, 1800 K和10-10Pa).在富氧条件下(图4a1),本文研究结果与Zheng等30在极限条件下的研究结论基本一致.在图4c3低氧分压下,当费米能级在接近价带时,为最稳定缺陷(Zheng等30的研究结论是为最稳定点缺陷,和形成能相差极小),随着费米能级的增加,替代成为最主要点缺陷,跟Zheng等的研究结果基本一致.本文中当费米能级继续增加时,最稳定点缺陷为而Zheng等的研究结果为(随着费米能级的增加最稳定缺陷依次为由于Zheng等的结论是在缺氧极限条件下得到的,比本文给出的化学势更低,所以得到比更加稳定的结论,与的缺陷形成能几乎相等,说明了氧分压对缺陷形成能有非常重要的作用.
通过比较图4中c1,c2和c3,当温度不变时,的缺陷形成能改变很明显,而的缺陷形成能只改变1 eV,从中可以得出对氧分压比敏感得多.这是由于随着氧分压的改变,O和Hf的化学势都发生改变,而改变的大小趋势是相反的.
图5描述的是在几种典型的不同费米能级EF下,最稳定的点缺陷在氧偏压和温度的二维空间的分布,结合4个图可以看出最稳定点缺陷随着费米能级而改变.在费米能级为0.50 eV时,随着温度下降氧分压上升,出现的最稳定点缺陷分别是和(图5a)(跟Zheng等30的研究结果即在缺氧、一般条件和富氧条件下价带附近出现的最稳定点缺陷吻合),与三维图吻合.即在650到1800 K温度区间,10-8.5到0 Pa氧分压条件下,是最主要的稳定点缺陷.当费米能级为1.00 eV时,最稳定点缺陷只有和(图5b).费米能级增加到1.50 eV时,在氧化条件下开始出现(图5c).在还原条件下,费米能级为0.50、1.50和3.40 eV时,对应的最稳定本征点缺陷为和从图5d中可以看出当费米能级超过3.40 eV时,是最主要的点缺陷.这个结果进一步说明了本征缺陷的分布对微小变化的杂质和缺陷浓度引起的费米能级变化非常敏感.
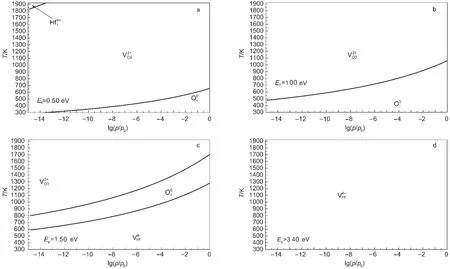
图5 四种不同费米能级下计算的温度与氧分压的缺陷形成能二维图Fig.5 Two-dimensional defect formation energies as functions of temperature and oxygen partial pressure calculated at four different Fermi levels
前文讨论了本征点缺陷随环境条件和费米能级变化的基本规律.然而,根据晶体局部电中性的要求,带电点缺陷一般不会孤立存在于晶体中,而是作为电中性缺陷族的一部分,其中最典型的就是弗伦克尔、反弗伦克尔和肖特基缺陷.本文采用如下方法计算弗伦克尔、反弗伦克尔和肖特基的缺陷形成能这里Etotal(α,q)和Etotal(perfect)跟方程(1)的意义相同,其中为弗伦克尔缺陷,为反弗伦克尔缺陷,为肖特基缺陷,-q为带电荷数,µHf与µO分别为Hf与O的化学势.
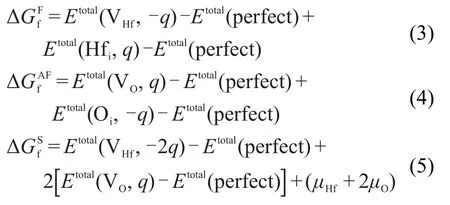
这里的缺陷族是考虑带电缺陷或者电中性缺陷的结合,而缺陷族的总带电量为零.因此,对三种不同的弗伦克尔缺陷进行考虑:和反弗伦克尔缺陷和肖特基缺陷组合方法类似,由于缺陷族的总带电量为零,所以不需要再考虑费米能级的作用,缺陷簇形成能如图6所示.
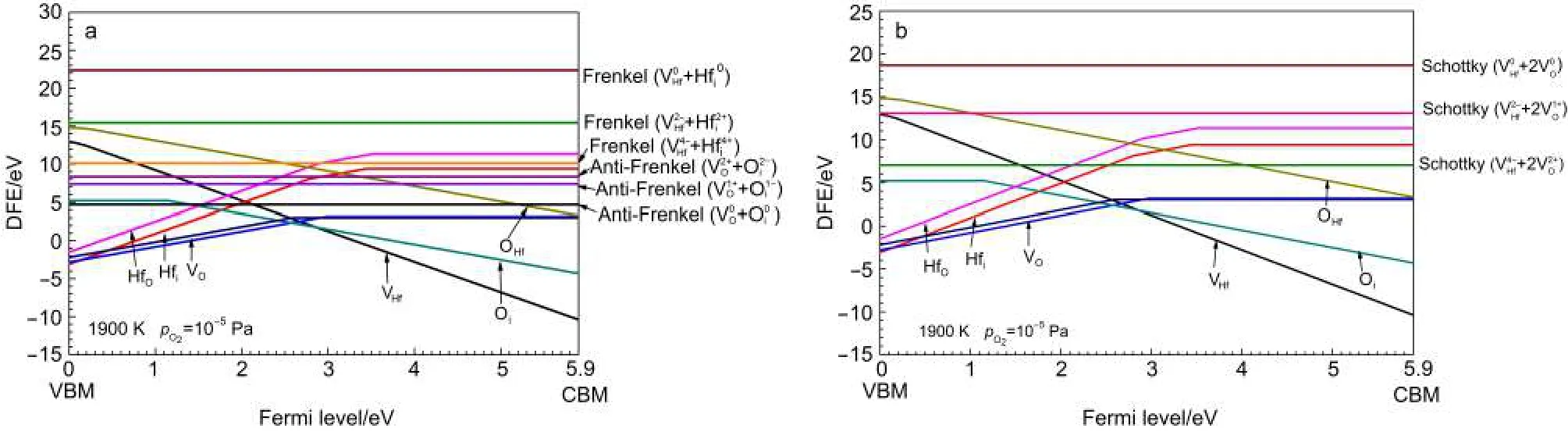
图6 计算的缺陷族形成能Fig.6 Calculated defect formation energies of defect complexes
从图6中可以发现,对于弗伦克尔缺陷和肖特基缺陷,带电缺陷结合的缺陷族形成能比中性缺陷结合的缺陷族的形成能低.例如,的形成能比的形成能低,而对于反弗伦克尔则有相反的规律,如图6a,的形成能明显比低.从图中可以知道,反弗伦克尔缺陷总比弗伦克尔缺陷更易形成,并且和异常接近.而从图6b中可以看到不同的肖特基缺陷族的形成能相差很大,从7.01到18.67 eV范围变化.
4 结论
基于密度泛函理论,结合热力学方法,在温度、氧分压和费米能级三者都连续变化时,对HfO2的本征点缺陷进行研究.通过作图分析发现:随着温度、氧分压和费米能级的改变,最稳定点缺陷也随着改变,在同等条件下(富氧和缺氧),本文得到的结论与实验及其它课题组的结论基本一致.而本文给出了一般条件下点缺陷的分布规律.该晶体中的主要点缺陷都是只有带偶数电荷时是稳定的,这体现为negative-U特性,与实验结果一致.从三维图中可知,和占据三维空间的大部分区域,即和是HfO2的主要本征点缺陷.在费米能级大于3.40 eV时,不管温度和氧分压如何变化,都是主要点缺陷.在缺陷族中,反弗伦克尔缺陷比弗伦克尔缺陷更加稳定,而不同类型的肖特基缺陷形成能变化很大.在HfO2晶体所有本征点缺陷中,对于温度、氧分压和费米能级都非常敏感.
(1)Chow,R.S.;Falabella,G.E.;Loomis,F.;Rainer,C.J.;Stolz, M.;Kozlowski,R.Appl.Opt.1993,32,5567.doi:10.1364/ AO.32.005567
(2)Waldorf,A.J.;Dobrowolski,J.;Sullivan,A.B.T.;Plante,L.M. Appl.Opt.1993,32,5583.doi:10.1364/AO.32.005583
(3)Houssa,M.High-k Gate Dielectrics;Institute of Physics: Bristol and Philadelphia,2004.
(4)Copel,M.;Gribelyuk,M.;Gusev,E.Appl.Phys.Lett.2000,76, 436.doi:10.1063/1.125779
(5)Jeon,T.S.;White,J.M.;Kwong,D.L.Appl.Phys.Lett.2001,78,368.doi:10.1063/1.1339994
(6)Qi,W.J.;Nieh,R.;Lee,B.H.;Kang,L.;Joen,Y.J.;Lee,J.C. Appl.Phys.Lett.2000,77,3269.doi:10.1063/1.1326482
(7)Gusev,E.P.;Cartier,E.D.;Buchanan,A.;Gribelyuk,M.; Copel,M.;Okorn-Schmidt,H.;Emic,C.D.Microelectron.Eng.2001,59,341.doi:10.1016/S0167-9317(01)00667-0
(8)Wilk,G.D.;Wallace,R.M.;Anthony,J.M.J.Appl.Phys.2001,89,5243.doi:10.1063/1.1361065
(9)Houssa,M.;Afanas'ev,V.V.;Stesmans,A.;Heyns,M.M.Appl. Phys.Lett.2000,77,1885.doi:10.1063/1.1310635
(10)Lee,B.H.;Kang,L.;Nieh,R.;Qi,W.J.;Lee,J.C.Appl.Phys. Lett.2000,76,1926.doi:10.1063/1.126214
(11)Gusev,E.P.;Cabral,C.;Copel,J.M.;D'Emic,C.;Gribelyuk, M.Microelectron.Eng.2003,69,145.doi:10.1016/S0167-9317 (03)00291-0
(12)Lee,S.J.;Jeon,T.S.;Kwong,D.L.;Clark,R.J.Appl.Phys.2002,92,2807.doi:10.1063/1.1500420
(13)Kukli,K.;Ritala,M.;Sundqvist,J.;Aarik,J.;Lu,J.;Sajavaara, T.;Leskela,M.;Harsta,A.J.Appl.Phys.2002,92,5698.doi: 10.1063/1.1515107
(14)Cho,M.H.;Roh,Y.S.;Whang,C.N.;Jeong,K.;Nahm,S.W.; Ko,D.H.;Lee,J.H.;Lee,N.I.;Fujihara,K.Appl.Phys.Lett.2002,81,472.doi:10.1063/1.1487923
(15)Kim,J.;Kim,S.;Jeon,H.;Cho,M.H.;Chung,K.B.;Bae,C. Appl.Phys.Lett.2005,87,053108.doi:10.1063/1.2005370
(16)Lee,S.J.;Choi,C.H.;Kamath,A.;Clark,R.;Kwong,D.L. IEEE Electron Device Lett.2003,24,105.doi:10.1109/ LED.2002.807712
(17)Huff,H.R.Microelectron.Eng.2003,69,152.doi:10.1016/ S0167-9317(03)00292-2
(18)Busch,B.W.;Schulte,W.H.;Garfunkel,E.;Gustafsson,T.;Qi, W.;Nieh,R.;Lee,J.Phys.Rev.B2000,62,13290.doi:10.1103/ PhysRevB.62.R13290
(19)Brossman,U.;Wurschum,R.W.;Sodervall,U.;Schaefer,H.E. J.Appl.Phys.1999,85,7646.doi:10.1063/1.370567
(20)Martin,D.;Duprez,D.J.Phys.Chem.1996,100,9429.doi: 10.1021/jp9531568
(21)Chavez,J.R.;Devine,R.A.B.;Koltunski,L.J.Appl.Phys.2001,90,4284.doi:10.1063/1.1401796
(22)Foster,A.S.;Sulimov,V.B.;Gejo,F.L.;Shluger,A.L.; Nieminen,R.M.Phys.Rev.B2001,64,224108.doi:10.1103/ PhysRevB.64.224108
(23)Deng,Z.W.;Guo,W.M.;Liu,H.M.;Cao,L.L.Acta Phys.-Chim.Sin.1999,15,528.[邓宗武,郭伟民,刘焕明,曹立礼.物理化学学报,1999,15,528.]doi:10.3866/PKU. WHXB19990609
(24)Wang,F.F.;Cao,Z.M.;Chen,J.;Xing,X.R.Acta Phys.-Chim. Sin.2014,30,1432.[王方方,曹战民,陈 骏,邢献然.物理化学学报,2014,30,1432.]doi:10.3866/PKU. WHXB201405281
(25)Robertson,J.;Xiong,K.;Falabretti,B.IEEE Trans.Device Mater.Reliab.2005,1,84.
(26)Xiong,K.;Robertson,J.;Gibson,M.C.;Clark,S.J.Appl.Phys. Lett.2005,87,183505.doi:10.1063/1.2119425
(27)Foster,A.S.;Gejo,F.L.;Shluger,A.L.;Nieminen,R.M.Phys. Rev.B2002,65,174117.doi:10.1103/PhysRevB.65.174117
(28)Shen,C.;Li,M.F.;Wang,X.P.;Yu,H.Y.;Feng,Y.P.;Lim,A. T.L.;Yeo,Y.C.;Chan,Y.D.S.H.;Kwong,D.L.Tech.Dig. Int.Electron Devices Meet.2004,733.
(29)Kang,J.;Lee,E.C.;Chang,K.J.;Jin,Y.G.Appl.Phys.Lett.2004,84,3894.doi:10.1063/1.1738946
(30)Zheng,J.X.;Ceder,G.;Maxisch,T.;Chim,W.K.;Choi,W.K. Phys.Rev.B2007,75,104112.doi:10.1103/PhysRevB.75. 104112
(31)Perdew,J.P.;Burke,K.;Ernzerhof,M.Phys.Rev.Lett.1996,77,3865.doi:10.1103/PhysRevLett.77.3865
(32)Kresse,G.;Furthmüller,J.Phys.Rev.B1996,54,11169.doi: 10.1103/PhysRevB.54.11169
(33)Kresse,G.;Joubert,D.Phys.Rev.B1999,59,1758.
(34)Blöchl,P.E.Phys.Rev.B1994,50,17953.doi:10.1103/ PhysRevB.50.17953
(35)Lee,J.;Han,S.Phys.Chem.Chem.Phys.2013,15,18906.
(36)Batyrev,I.G.;Alavi,A.;Finnis,M.W.Phys.Rev.B2000,62, 4698.
(37)Finnis,M.W.;Lozovoi,A.Y.;Alavi,A.Ann.Rev.Mat.Res.2005,35,167.doi:10.1146/annurev.matsci.35.101503.091652
(38)Lide,D.R.CRC Handbook of Chemistry and Physics,Internet Version 2005(http://www.hbcpnetbase.com);CRC Press:Boca Raton,FL,2005.
Prediction of Native Point Defects in HfO2Crystals Using First Principles and Thermodynamic Calculations
LIU Feng-Ming LIU Ting-Yu*LIU Jian LI Hai-Xin
(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,P.R.China)
Based on first principles and thermodynamics the intrinsic point defect formation energy was calculated at different temperatures and oxygen partial pressures in HfO2crystals.The stability of all kinds of point defects as well as the formation of charged point defects and their sensitivity to the Fermi energy was analyzed.We also discuss rules that govern the formation of various point defects that vary with Fermi level. The results show that with a change in temperature and oxygen partial pressure the most stable point defects are obtained(O0i,V2+O3and Hfi4+)when the Fermi level is close to the valence band.The main point defect was the Hf vacancy at a-4 charge when the Fermi level was higher than 3.40 eV.Apart from the Hf vacancy almost no other point defect had an odd charge and they showed negative-U behavior.Using the most stable intrinsic defect as a function of the Fermi level,the oxygen partial pressure and the temperature were determined using three-dimensional defect formation enthalpy diagrams.This diagram provides information that allows for the control of point defects in the crystal.
Density functional theory;Point defect;Thermodynamics;HfO2crystal
The project was supported by the Foundation of Hujiang,China(B14004).
沪江基金(B14004)资助项目
O641
10.3866/PKU.WHXB201412301www.whxb.pku.edu.cn
Received:October 8,2014;Revised:December 30,2014;Published on Web:December 30,2014.∗
