抛物线内切伴随圆族的方程及性质
2015-12-29田颖辉
田颖辉
(阜新高等专科学校,辽宁阜新123000)
曲线的伴随圆是指与曲线相关的圆.文献[1]探讨了抛物线的一类伴随圆——内切圆族的方程和性质.在此基础上,笔者对抛物线y2=2px(p>0)的内切伴随圆族的方程与性质进行了进一步的探讨,得到了一些结论.
1 相关定义
1.1 内切圆
在抛物线的内部,与抛物线有且只有一个交点的圆,叫做抛物线的内切圆(图1).
1.2 内切圆族
与抛物线内切,且具有共性的一族圆称为抛物线的内切圆族(图1).
2 相切于一点的内切圆族

图1 内切圆与内切圆族
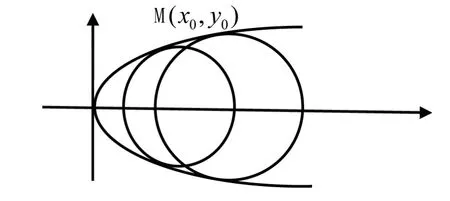
图2 引理1内切圆族
引理1[1]设抛物线C的方程为y2=2px(p>0),设M(x0,y0)是抛物线上的一点,则与抛物线内切圆族的方程为(x-p-x0)2+y2=p2+2px0(x0是参数,x0≥0),其圆心轨迹为以(p,0)为端点且与x轴正方向同向的射线.
引理中所描述的内切圆族情形如图2所示.
由引理1可知,对于抛物线上的固定点M(x0,y0),其内切圆为(x-p-x0)2+y2=p2+2px0(x0≥0),点(x0,y0)关于x轴的对称点为(x0,-y0)也在圆上,显然,该圆是内切于M(x0,y0)的圆中最大的内切圆.
定理1 设抛物线C:y2=2px(p>0),内切于抛物线上的定点M(x0,y0)的最大内切圆为

在圆(Ⅰ)内部可作一系列与点M(x0,y0)相切的圆,显然这些圆都是抛物线的内切圆,它们构成了一类抛物线的内切伴随圆族(图3).
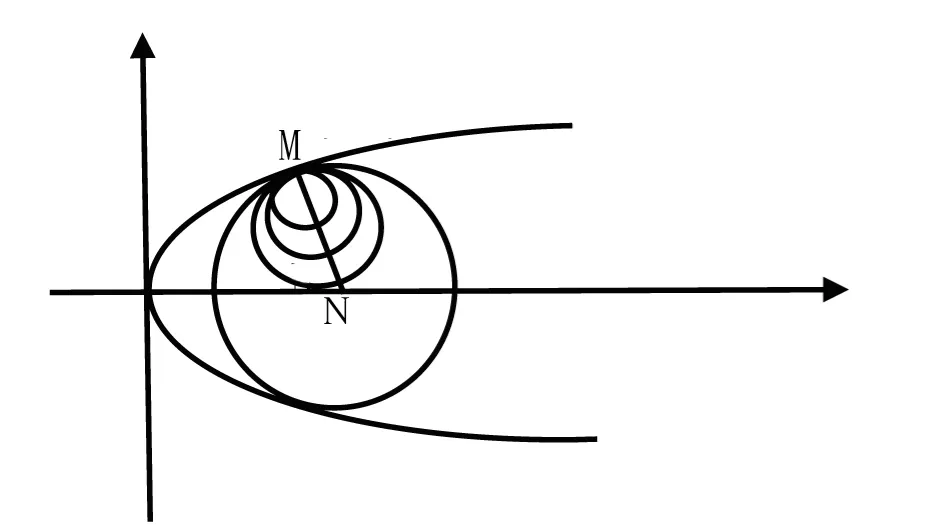
图3 定理1抛物线的内切伴随圆族
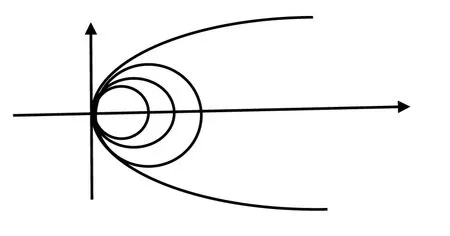
图4 推论3内切伴随圆族
推论1 与抛物线C:y2=2px(p>0)相切于抛物线上的定点M(x0,y0)的内切伴随圆族的圆心轨迹为线段MN(去掉端点M),其中N(x0+p,0)(图3).
令x0=0,则y0=0,即此时M点为抛物线的顶点(0,0),由此得如下结论.
推论2 与抛物线C:y2=2px(p>0)相切与顶点的最大内切伴随圆为(x-p)2+y2=p2.
推论3 与抛物线C:y2=2px(p>0)相切与顶点的内切伴随圆族的方程为(x-a)2+y2=a2(0<a≤p)(图4).
3 以定长为半径的内切伴随圆族
抛物线C:y2=2px(p>0)的最大内切圆族中最小的一个圆的半径为p,这里仅取定长r(0<r≤p)为半径作抛物线的内切伴随圆.当该圆沿抛物线内侧移动时,这些圆是抛物线的一类内切伴随圆族.
定理2 半径为定长r(0<r≤p),与抛物线C:y2=2px(p>0)内切伴随的圆族的圆心方程为

证明 设抛物线C的参数方程为
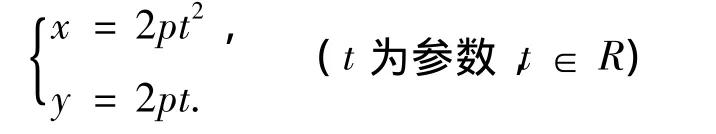
定长为r(0 < r≤p),圆心为(x0,y0)的圆方程为(x-x0)2+(y-y0)=r2,与抛物线C内切于点(x1,y1).过点(x1,y1)与抛物线相切的直线的斜率为k=y'=,则
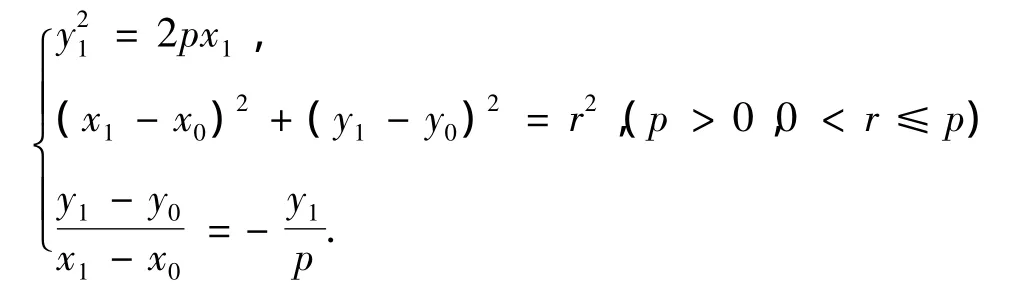
解方程组得

由于内切圆心位于抛物线内,且在过切点(x1,y1)的法线上,所以x0>x1将x1=2pt2,y1=2pt代入上式,最终得到定长为r的内切伴随圆的圆心参数方程
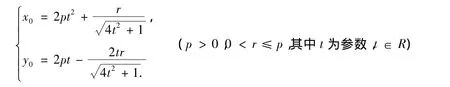
其圆心轨迹是夹在抛物线y2=2px(p>0)与抛物线y2=2(p-r)x间的类似抛物线(p>0,0<r≤p),随着r的增减在两抛物线间伸缩(图5,图6).
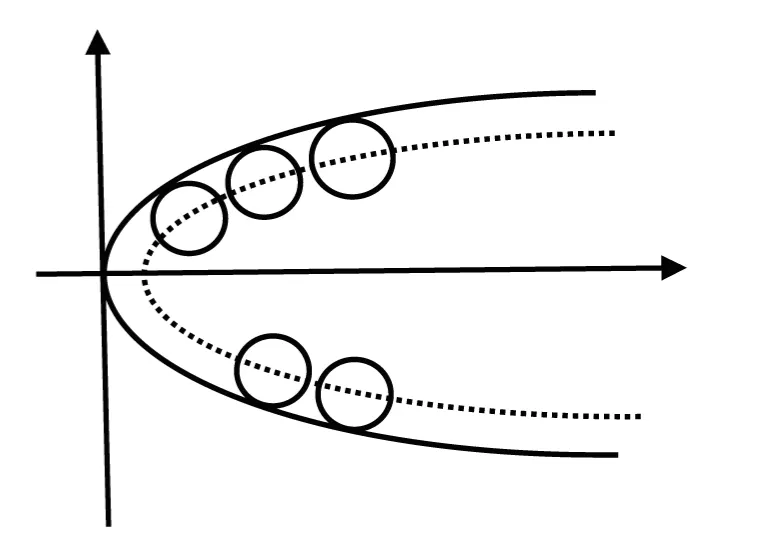
图6 抛物线的一类内切伴随圆族随着r减小的圆心轨迹

图5 抛物线的一类内切伴随圆族随着r增加的圆心轨迹
[1]刘耀斌,顾越岭.抛物线的伴随圆系及其性质[J].数学通报,2007,46(3):38 -40.
[2]梁双凤,李宝荣,梁林.椭圆的内切圆与曲率圆的方程及图像研究[J].玉溪师范学院学报,2010,26(8):8-13.
