灵活选用 简捷解题
2015-12-28李君
李君
苏科版八年级上册第97页中有这样一道题:
在△ABC中,∠C=90°.
(1) 已知AC=5,BC=12,求AB;
(2) 已知AC=2,BC=3,求AB;
(3) 已知AB=25,AC=24,求AC.

本题是勾股定理的应用,即可以直接应用勾股定理的表达式a2+b2=c2来解决,但在上述解题过程中,我们应用了它的变式:c= ,b= .很明显,这样的解题过程更简捷.因此,我们在解题时,要注意根据题目的具体特点来选择勾股定理的表达式及其变式,以优化解题过程.下面举例说明.
例1 如图1,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M表示的数是( ).
【点评】这是在数轴上寻找表示无理数的点,说明数轴上的点与实数是一一对应的,体现了数形结合的思想.
例2 在Rt△ABC中,已知两边长分别是5和12,则其周长为________.
【分析】5和12可以是直角边,也可以是一条斜边和一条直角边,分两种情况用勾股定理表达式的变式求解较简捷.
解:当5和12为直角边时,由勾股定理表达式的变式可知,斜边为 =13,此时Rt△ABC的周长为5+12+13=30;当12为斜边时,5为直角边,则由勾股定理表达式的变式可知,另一条直角边为 ,此时Rt△ABC的周长为5+12+ .综上,周长为30或17+ .
【点评】已知直角三角形两边长求第三边,要注意分两种情况思考:一是这两边为直角边,二是这两边中较大边为斜边,较小边为直角边,要谨防漏解.
例3 (2015·江苏泰州)如图2,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为_______.
【分析】设BE交CD于点G,由折叠的性质可知EP=AP,∠E=∠A=90°,BE=AB=8,由ASA可证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=6-x,DG=x,求出CG、BG,再由勾股定理的表达式列方程求解较简捷.
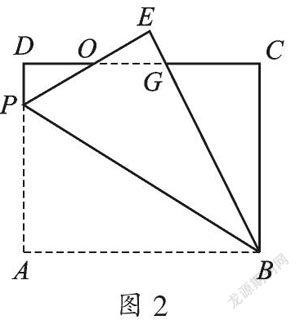
解:∵四边形ABCD是矩形,∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,根据题意得△ABP≌△EBP,∴EP=AP,∠E=∠A=90°,BE=AB=8,又△ODP≌△OEG(ASA),∴OP=OG,PD=GE,∴DG=EP,设AP=EP=x,则PD=GE=6-x,DG=x,∴CG=8-x,BG=8-(6-x)=2+x,根据勾股定理得:BC2+CG2=BG2,即62+(8-x)2=(x+2)2,解得:x=4.8,∴AP=4.8.
【点评】熟练掌握翻折变换和矩形(长方形)的性质,借助AP=x,并用x表示出其他未知量,再利用勾股定理列出方程是解决问题的关键.
(作者单位:江苏省兴化市楚水初级中学)
