切比雪夫多项式在精密星历拟合中的应用

张 奇李慕清李立瑞赖山东

（1.中南电力设计院 湖北武汉 430000；2.江西省基础测绘院 江西南昌 330001）

切比雪夫多项式在精密星历拟合中的应用

张 奇1李慕清1李立瑞1赖山东2

（1.中南电力设计院 湖北武汉 430000；2.江西省基础测绘院 江西南昌 330001）

在GPS高精度定位中，通常采用精密星历来获取观测卫星的位置。而当前一些国际组织发布的精密星历的采样率有限，因此，在GPS数据后处理中，用户需要采用一定的方法才能获得任意时刻卫星的位置。采用切比雪夫正交多项式来拟合卫星的轨道，其精度完全符合要求。

精密星历拟合；切比雪夫

1 引言

在GPS测量中，卫星坐标的计算是一项基本的工作。目前主要利用广播星历和精密星历来获取卫星的位置信息，前者是调制在导航电文中通过卫星实时播发给用户，其精度较低，约为2m，难以满足高精度定位用户的要求。鉴于此，IGS (TheInternationalGNSSService，国际GNSS服务)等国际组织发布了GPS精密星历，其最终精度优于5cm，被广泛应用于高精度定位中。然而，IGS精密星历是以15分钟的采样率给出卫星在ITRF(InternationalTerrestrial ReferenceFrame，国际地球参考框架)中的三维坐标及卫星钟差，在GPS数据后处理中用户需要选择合适的方法才能获得任意时刻观测卫星的位置信息。本文将采用切比雪夫正交多项式来拟合GPS卫星轨道，并对其精度进行分析。

2 切比雪夫多项式拟合的原理

切比雪夫多项式拟合就是根据给定的数据拟合出一个函数，使其在给定点的函数值与给定值之间的方差和最小，且该函数是以切比雪夫多项式为基函数构成的函数。第一类切比雪夫多项式定义为：

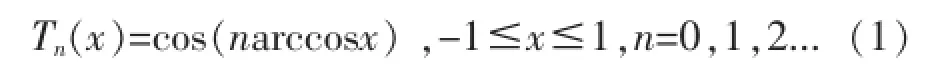
本文主要采用第一类切比雪夫多项式为基函数来拟合卫星轨道，以下简称切比雪夫多项式。

GPS卫星的轨道变化是一个连续的过程。因此，可以将卫星星历表示为时间的一个函数，将一定时间间隔的卫星坐标拟合成一个关于时间的多项式，在以后需要计算卫星坐标时只要调出多项式系数就可以计算得到卫星坐标，这大大提高了数据处理的效率。

假设需要在时间间隔［t0，t0+△t］内计算n阶切比雪夫多项式系数。其中t0为起始历元时刻，△t为拟合时间区间的长度。首先将变量t∈［t0，t0+△t］变换成τ∈［-1，1］：

则卫星的坐标X、Y、Z可表示为：

式中，n为切比雪夫多项式的阶数。CXi、CYi、CZi分别为X坐标分量、Y坐标分量、Z坐标分量的切比雪夫多项式系数。

切比雪夫多项式Ti可以根据递推公式求得

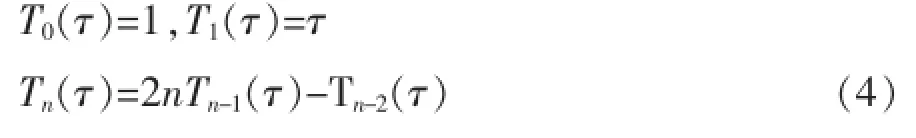
下面仅以X坐标分量为例叙述求解切比雪夫多项式系数的步骤。

根据精密星历提供的τk（k=1，2…m）时刻的卫星位置（Xk，Yk，Zk）组成坐标文件。设Xk为观测值，则误差方程为

则误差方程可写为：V=BM-L

由最小二乘原理可得：M＝（BTB）-1BTL

同理，Y、Z分量的切比雪夫多项式拟合系数也可求得。根据求得的切比雪夫多项式拟合系数CXi、CYi、CZi和式（2）、（3）和（4）即可求得计算区间［t，t+△t］内任意时刻的卫星坐标。

3 算例分析

本文采用从中国地壳运动观测网络（www.igs. org.cn）下载的2008年3月20日全天的精密星历数据（SP3格式）进行分析。数据包括32颗卫星的精密坐标，采样率为15分钟。现把PG02卫星的坐标数据拟合成采样间隔为1分钟的坐标数据。

为了验证算法的精度，采用拟合差表示算法的精度，拟合差是指精密星历提供的坐标值与对应时刻的拟合值的差值。如图1为采用15阶切比雪夫多项式时X、Y、Z分量的拟合差值图，横轴为时刻（从0时到23时45分，用累计分钟数表示时刻），纵轴为拟合差，单位为米。

从图1可以看出，15阶切比雪夫拟合多项式的精度比较低，只能达到米级。由于切比雪夫多项式的阶数与所选取的时间间隔都会对拟合精度产生影响，下面将对两者分别进行试验分析。图2、图3和图4分别18、20、25阶时X分量的拟合差值图（拟合时间间隔为1分钟）。

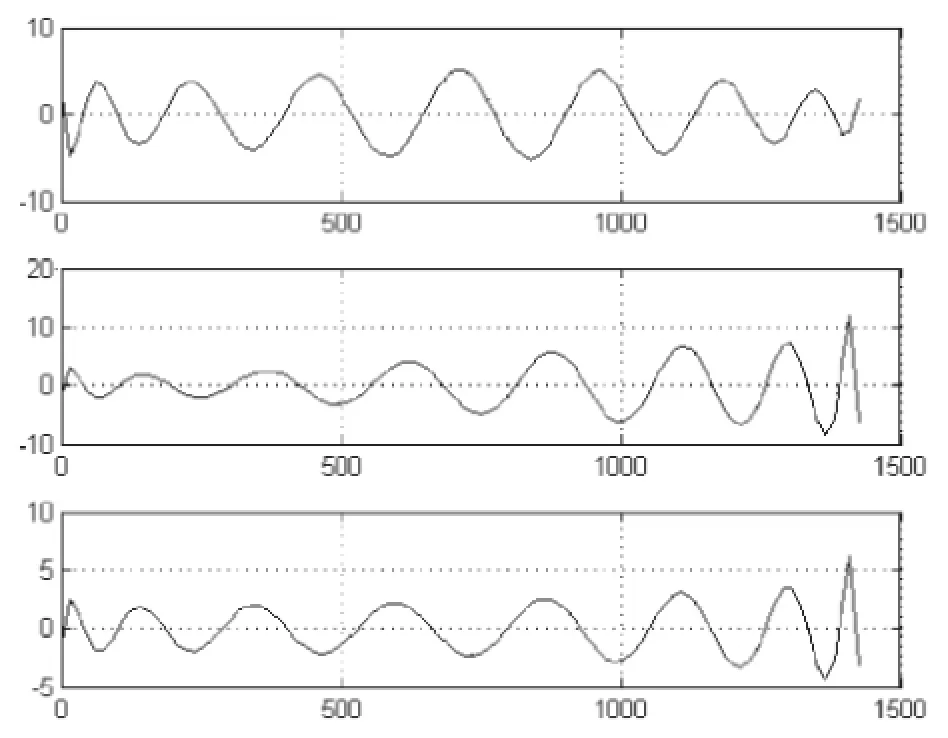
图1 采用15阶切比雪夫多项式时X、Y、Z分量的拟合差值图

图2 采用18阶切比雪夫多项式时X分量的拟合差值图

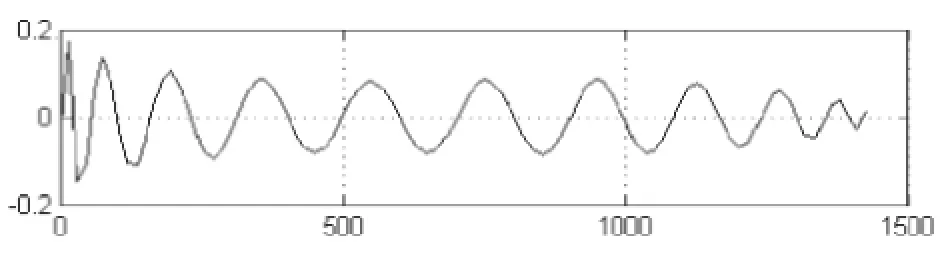
图3 采用20阶切比雪夫多项式时X分量的拟合差值图

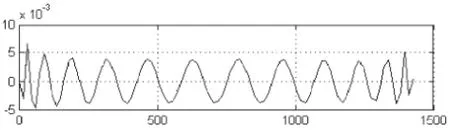
图4 采用25阶切比雪夫多项式时X分量的拟合差值图

从图2、图3和图4可以看出，拟合阶数越高，拟合差越小，拟合精度越高。本例中当取到21阶时，拟合差已经达到厘米级；取到25阶时，拟合差已经达到毫米级，满足实际应用的要求，继续增加拟合阶数，已经没有实际意义。

当固定拟合阶数为20阶时，分别选取1分钟、3分钟、5分钟的时间间隔，分量的拟合差如图5、图6和图7。

图5 采用20阶切比雪夫多项式1分钟时间间隔时X分量的拟合差值图

图6 采用20阶切比雪夫多项式3分钟时间间隔时X分量的拟合差值图

图7 采用20阶切比雪夫多项式5分钟时间间隔时X分量的拟合差值图

从图5、图6、图7可以看出，分别取1分、3分、5分的时间间隔时，拟合差值图没有变化。在计算中也发现，时间间隔对拟合差值影响不大。

4 结论

从以上的算例分析中可以得到以下结论：

4.1 利用切比雪夫多项式拟合精密星历是可行的，当取到一定阶数后，精度能满足要求；

4.2 在本文的算例分析计算中发现，切比雪夫多项式的阶数越高，拟合精度越高。如本例中，当阶数从20增加到25时，拟合精度从分米级提高到毫米级；

4.3 在本文算例中，拟合时间间隔的大小对拟合精度影响不大；而拟合时间间隔对任意时刻的卫星坐标精度的影响程度，由于不知道真实的卫星坐标，其大小也未知；

(4)本文的结论都是基于试验得到的，在实际的计算中，拟合阶数取到多少才合适还应根据具体的试验确定。

［1］李庆扬，王能超，等.数值分析［M］.北京:清华大学出版社，2001.

［2］余鹏，孙学金，赵世军.GPS定位中卫星坐标计算的切比雪夫多项式拟合法［J］.气象科技.2004年6月，第32卷，第3期.