形变方式对H62黄铜模压形变等效应变分布的影响
2015-12-28张植琼林雪慧
张植琼,林雪慧,2
(1. 福州大学 机械工程及自动化学院,福建 福州 350108; 2. 江汉大学 化学与环境工程学院,湖北 武汉 430056)
形变方式对H62黄铜模压形变等效应变分布的影响
张植琼1,林雪慧1,2
(1. 福州大学 机械工程及自动化学院,福建 福州 350108; 2. 江汉大学 化学与环境工程学院,湖北 武汉 430056)
摘要:采用三维有限元法(FEM)模拟H62黄铜交叉模压形变过程和平行模压形变过程,分析了这两种不同模压形变方式对试样模压形变后等效应变分布的影响,并与试验结果进行了比较。结果表明,随着模压周期的增加,与平行模压形变相比,交叉模压形变方式下试样等效应变累积值会更高,等效应变分布也会更均匀;其模拟结果中等效应变的分布规律与试验材料显微硬度的分布规律相对应。
关键词:H62黄铜;模压形变;有限元;等效应变
0引言
模压形变技术是Shin[1]等人提出的一种大塑性变形方法,它可以实现将金属材料晶粒细化到亚微米级甚至纳米级,从而获得物理和力学等各方面性能都很优异的超细晶材料[2]。与其他大塑性变形方法相比,由于模压形变技术具有工艺简单,生产成本低的特点而逐渐引起人们的关注,目前已应用该技术成功制备了超细晶纯铝和纯铜等材料[3-5]。苏丽凤[6]等人首次将模压形变法应用在对H62黄铜的细化研究上,并取得了很好的成果,相继研究了材料厚度[7]、模齿宽度[8]和模压道次[9]对模压形变的影响,并应用有限元法模拟了模压形变过程[9],对了解模压形变的实质和对试验的指导很有帮助,所以利用有限元法对模压形变过程进行模拟很有必要。
张莹[10]等人在平行模压形变的基础上提出了交叉模压形变方法,发现利用交叉模压形变方法获得的试样比平行模压形变后的试样具有更好的组织均匀性和更高的硬度值。为了更好地了解两者的差异,采用ABAQUS软件模拟在这两种模压形式下的H62黄铜模压形变过程,分析不同形变方式下试样等效应变的分布规律,并与试验结果进行对比,为研究其他材料的模压形变过程打下基础。
1模型建立
1.1模压形变工艺原理
模压形变工艺的原理如图1所示,图1(a)为模压形变工艺初始装配状态,其中弯模模具的倾角θ为45°,锯齿齿宽为t,板状试样置于两弯模中间。1) 进行第1次压弯过程(图1(b)),使平台部分的试样不发生变形,在模具倾斜面部分的试样受到剪切变形,累积等效应变为0.58。2) 如图1(c)所示,使用一对平模将试样压平,倾斜部分受到反向的剪切变形,积累等效应变为1.16,而平台部分试样的等效应变仍为0。3) 移动试样一个齿宽t的距离(图1(d)),再进行第2次压弯、压平,使未变形的部分累积等效应变为1.16,这样整个试样累积的等效应变均为1.16,以上所述过程称为1周期平行模压形变过程。如果在进行1周期平行模压形变之后,将试样沿y轴旋转90°,再经过1周期的平行模压形变,则称之为1周期的交叉模压形变过程。试样进行多周期模压形变处理,可以在试样上累积大的等效应变。
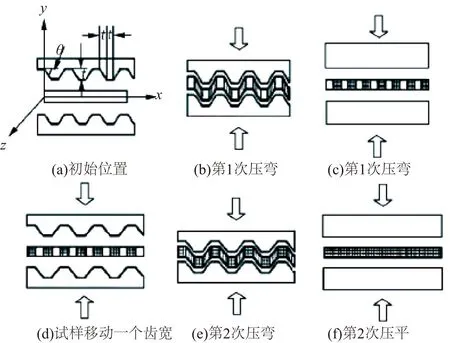
图1 模压形变示意图
1.2有限元模型的建立
由于交叉模压变形要绕着y轴旋转90°,因此,采用ABAQUS软件中弹塑性三维有限元模型模拟交叉模压形变过程,而平行模压形变过程虽然可近似认为沿着z方向的变化是一致的而采用二维有限元模型模拟,但是为了能和交叉模压形变过程进行很好的比较,也采用三维有限元模拟平行模压形变过程。两种模压形变采用的试样尺寸为50mm×50mm×2mm,采用C3D8R单元划分网格,单元尺寸为0.5mm,单元形状为六面体,初始单元数为40000个。模型中弯模齿宽t为7mm,倾角θ为45°。模具定义为解析刚体,不需要进行网格划分和单元选择。令试样和模具之间接触的摩擦系数为0.1(金属冷成型过程中摩擦系数范围为0.05-0.15)。赋以试样为黄铜材料,即弹性模量为105GPa,泊松比为0.3,模拟所用的真实应力-应变曲线如图2所示,该曲线是在Instron Model-1185型万能机上单向拉伸H62黄铜试验获得。真实应变εtrue是由塑性应变εpl和弹性应变εel两部分构成,在ABAQUS中定义塑性材料参数时,需要使用塑性应变εpl,其表达式为:
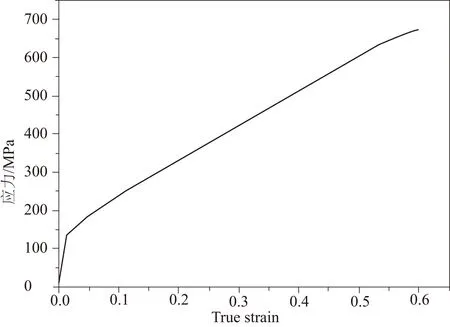
图2 H62黄铜的真实应力应变曲线
2模拟结果讨论
图3和图4分别为平行模压1周期和交叉模压1周期的等效应变分布云图。从图中可以看出,与图3相比,图4交叉模压1周期后,不论是长度方向还是宽度方向,其等效应变的分布均匀性得到了改善。同时,三维模拟交叉模压形变也存在着端部效应[9],即试样周围的等效应变积累量最小,试样中心区域等效应变累积量最大,其余部分则介于两者之间。这是因为整个交叉模压形变过程中试样周围未受到模具限制,可随着交叉模压形变过程的进行而自由伸长,大大降低了模具对其剪切和挤压作用;试样中心等效应变累积量最大部分在整个交叉模压形变过程中除了受到模具的挤压、剪切作用外,还受到周围试样的挤压及其内部金属流动的作用,使其等效应变累积量最大,且图中深色区域主要对应在模具齿顶拐角附近;随着与中心的距离的加大,试样受其内部挤压及金属流动作用逐渐变小,端部效应影响加大,使得试样其余部分的等效应变累积量逐渐变小。

图3 平行模压1周期后等效应变分布云图

图4 交叉模压1周期后等效应变分布云图
为了更清楚地了解交叉模压和平行模压这两种模压形式对试样经过多周期模压形变后等效应变分布的影响,图5给出了这两种模压形式下试样经等周期模压形变后沿长度方向等效应变分布曲线。由于同周期内,交叉模压形变压弯压平次数多于平行模压形变,通过图5(a)、图5(b)可以看出,经过1周期交叉模压形变处理后的试样上累积的等效应变明显多于平行模压形变处理的试样,尤其是试样中心,从这2个图还可以看出,两种模压形式下等效应变分布均匀性差不多,交叉模压的等效应变分布均匀性略好于平行模压。随着周期的增加即模压形变3周期后(如图5(c)、图5(d)所示),两种模压形式下等效应变累积值的差距会变小;对于均匀性,平行模压试样表面等效应变累积量稳定性很差,且各等效应变峰值间相差比较大,使得等效应变分布不均,严重影响材料的物理及力学性能,而经交叉模压形变处理后的试样,等效应变峰值间差距明显缩短,各点间等效应变值平稳过渡,不会存在过大的波动,使等效应变在整个试样上能够相对均匀分布。综上所述,随着周期的增加,交叉模压形变方式要比平行模压形变方式更能有效的改善等效应变在试样上的分布均匀性。
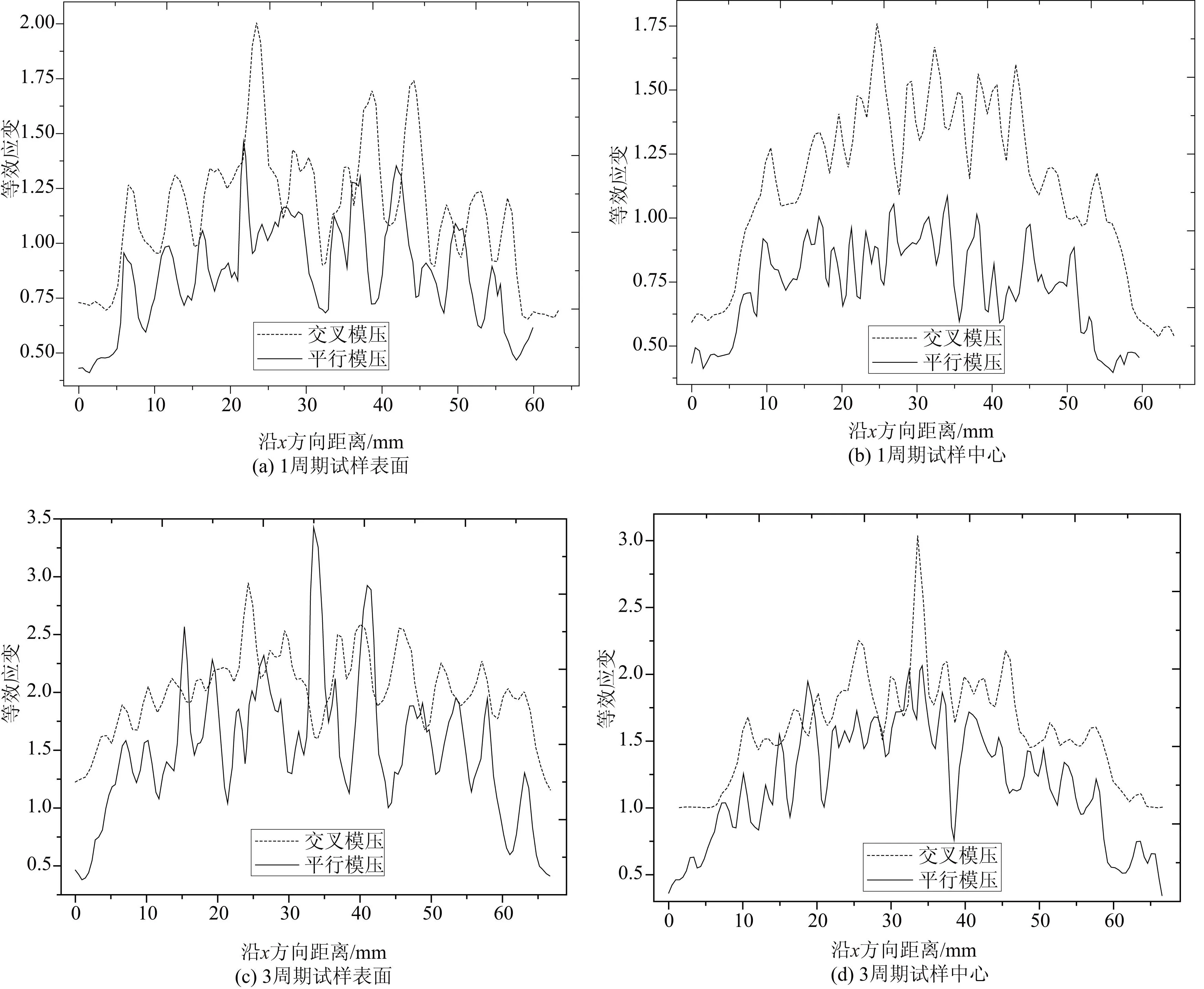
图5 不同形变方式下模压等周期后试样等效应变分布曲线
交叉模压1周期相当于平行模压2周期,其积累的等效应变很显然会高于平行模压1周期,为了得到在相同压弯压平次数后,两种模压形式对等效应变的影响,图6给出了4次压弯压平即交叉模压1周期和平行模压2周期后试样沿长度方向等效应变分布曲线图。通过几条曲线可以看出无论试样表面还是中心,交叉模压形变1周期后的等效应变累积量仍略高于平行模压形变2周期后的试样。平行模压形变2周期后,在试样表面部分区域的等效应变累积量值明显高于其他部分,严重影响了整个试样上等效应变分布的均匀性;在试样中间虽然不会出现等效应变值急剧升高的现象,但各点间的等效应变累积量还存在明显的差距。分析交叉模压形变1周期后的等效应变分布曲线,试样表面和中心上各点间等效应变值不会像平行模压处理的试样发生特别明显波动,说明经过1周期交叉模压形变处理后的试样,与平行模压2周期相比,不但在等效应变累积量上有所提升,等效应变分布均匀性也会得到明显改善。

图6 相同压弯压平次数后试样沿长度方向等效应变分布曲线
通过以上分析可知,不管是在相同压弯压平次数下还是相同周期下,与平行模压相比,采用交叉模压形变,能获得更高的等效应变累积值和更好的均匀性,这与张莹等人的试验结果(随着周期的增加,交叉模压形变方式所获得的试样比平行模压形变方式所获得的的试样有更好的均匀性和更高的硬度值)是相对应的。
3结语
1) 交叉模压1周期相当于平行模压2周期,即使在相同压弯压平条件下,交叉模压1周期试样累积的等效应变值仍略高于平行模压2周期试样,且等效应变分布均匀性也比平行模压方式下的试样要好。
2) 在相同周期条件下,交叉模压形变试样所获得的等效应变肯定会高于平行模压形变的试样,但是随着周期的增加,差距会缩小,除此之外,交叉模压形变试样等效应变分布均匀性比平行模压形变试样要好的多。
3) 模压形变有限元模拟结果中等效应变的分布规律与实际试验中显微硬度的分布规律是一致的。
参考文献:
[1] Shin D H, Park J J, Kim Y S, et al. Constrained groove pressing and its application to grain refinement of aluminum [J]. Materials and Science Engineering A, 2002, 328: 98-103.
[2] Valiev R Z. Structure and mechanical properties of ultra-fine grained metals [J]. Mater Sci Eng A,1997,234:59-66.
[3] Lee J.W,Park J.J. Numerical and experimental investigations of constrained groove pressing and rolling for grain refinement [J]. Journal of Materials Processing Technology,2002,130-131:208-213.
[4] Krishnaiah A,Chakkingal U,Venugopal P. Applicability of the groove pressing technique for grain refinement in commercial purity copper [J]. Materials Science and Engineering,2005,410-411:337-340.
[5] Krishnaiah A,Chakkingal U,Venugopal P. Production of ultrafine grain sizes in aluminum sheets by severe plastic deformation using the technique of groove pressing [J]. Scripta Materialia, 2005,52(12):12.
[6] 苏丽凤,彭开萍,肖林钢. 反复模压形变法细化H62黄铜的研究[J]. 机械工程材料,2007, 31(7):15-18.
[7] 曾佳伟,牟雪萍,彭开萍. 材料厚度对H62黄铜模压形变等效应变分布的影响[J]. 机械工程材料,2011,35(2):92-96.
[8] 张萤,彭开萍. 模齿宽度对模压变形纯铜晶粒尺寸与力学性能的影响[J]. 机械工程材料,2009,33(10):13-16.
[9] 曾佳伟,彭开萍. H62黄铜模压形变有限元模拟[J]. 金属热处理,2010,35(5):83-86.
[10] 张萤,彭开萍,林雪慧. 形变方式对模压形变H62黄铜组织的影响[J]. 材料热处理学报,2009,30(4):114-119.
Effect of Groove Pressing Mode on Distribution of Equivalent
Strain During Groove Pressing Process of H62 Brass
ZHANG Zhi-qiong1, LIN Xue-hui1,2
(1. School of Mechanical Engineering and Automation,Fuzhou University, Fuzhou 350108, China;
2. School of Chemical and Environmental Engineering, Jianghan University, Wuhan 430056, China)
Abstract:A three-dimensional finite element method is used to simulate the deformation process of H62 brass during cross groove pressing and parallel groove pressing. The influence of these two different groove pressing modes on equivalent strain distribution of the specimen after groove pressing is analyzed. and compared with the experimental results. The results shows that compared with the result of parallel groove pressing mode, the equivalent strain of the specimen after cross groove pressing is higher on cumulative value and more uniform on distribution with the increase of the grooving pressing cycles. The distribution of simulated equivalent strain is corresponded to the distribution of material micro hardness.
Keywords:H62 brass; groove pressing; finite element method; equivalent strain
收稿日期:2014-12-02
中图分类号:TP391.4
文献标志码:B
文章编号:1671-5276(2015)03-0127-04
作者简介:张植琼(1990-),女,湖北荆州人,硕士研究生,主要研究方向为新材料力学行为。
