基于故障树和模糊推理petri网的塞拉门系统可靠性分析
2015-12-28刘光武蔡昌俊陈刚杨玲芝邢宗义
刘光武,蔡昌俊,陈刚,杨玲芝,邢宗义
(1. 广州市地下铁道总公司,广东 广州 510030; 2. 南京理工大学 自动化学院,江苏 南京 210094)
基于故障树和模糊推理petri网的塞拉门系统可靠性分析
刘光武1,蔡昌俊1,陈刚1,杨玲芝1,邢宗义2
(1. 广州市地下铁道总公司,广东 广州 510030; 2. 南京理工大学 自动化学院,江苏 南京 210094)
摘要:对车门系统可靠性分析,提出了FTA定性分析和模糊推理Petri网定量分析相结合的方法。首先,在分析了车门系统的故障模式及故障事件的因果关系的基础上,建立了车门系统故障树模型;其次,通过FTA-FRPN的图形转化规则得到Petri网模型,最后,将模糊推理Petri网的推理算法应用于车门系统的可靠性分析,计算得到目标事件的故障率和初始事件的重要度及排序。结果验证了基于FTA和FRPN的可靠性分析方法的有效性,计算结果有助于技术人员和维修人员分析车门系统的运营状况。
关键词:可靠性分析;塞拉门;故障树分析;模糊Petri网
0引言
城市地铁车辆车门是复杂的机械和电气相结合的系统。由于地铁列车运营线路站距短,车门高频次地开启和关闭,极易导致车门的门控电气元件和机械零部件损坏,造成正线运营时列车车门故障频发,故障程度较轻的情形则需要切除该车门,故障较重则会导致列车的掉线、停运给正常的生活和城市的有序运转带来不利影响。对此,进行了车门可靠性研究。
近年国内外学者对车门系统可靠性进行了一些研究,朱小娟[1]、周俊龙[2]等通过建立地铁车门系统的故障树,分析得到导致车门故障的薄弱环节,以此给出了提高车门可靠性的建议。周黎明[3]提出用基于蒙特卡罗仿真和故障树分析的方法进行地铁车门可靠性分析。由于缺乏有效的数学表达方法,FTA方法不容易自动进行进一步的定量分析[4],无法有效地描述故障的传播。Petri网是对离散事件动态系统建模和分析的重要工具,而故障的产生和传播是一个典型的动态过程,利用Petri网可以很好地描述故障的产生和传播过程[5-7]。模糊推理Petri网的形式化推理算法,能很好地表示和处理模糊知识和模糊故障信息,可实现智能推理,准确有效地控制故障传播[8]。
在对地铁车辆进行故障模式分析的基础上,采用基于故障树和模糊推理Petri网的形式化推理算法,建立地铁车辆车门FRPN分析模型,定量分析车门系统的可靠性,据此给出提高系统可靠性的建议。
1FRPN及推理算法
1.1FRPN基本概念
模糊推理Petri网(FRPN, Fuzzy Reasoning Petri Net)是一个在Petri网基础上扩展而来的图形化的数学建模工具,非常适合于人类知识的表示和人工智能领域,被广泛应用于通信、制造、运输等领域。文中将模糊Petri网应用于更具一般性的推理过程中,运用矩阵运算来实现形式化推理,使模糊推理过程更加简单和易于实现。在一个FRPN模型中,在库所中标识的token的值与一个0到1之间的真实值关联,变迁与一个0到1之间的CF关联,CF表示变迁为真的置信度;而规则推理过程用推理Petri网中变迁的触发表示。FRPN定义为一个八元组:

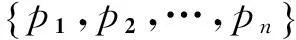
1.2FRPN的构建
在知识表达的模糊推理Petri网中,网的框架代表基于产生式规则的知识结构,故障树分析法(Fault Tree Analysis,简称FTA)是一种将系统故障原因按树枝状逐级细化的图形演绎方法。从推理机制与故障描述来看,FRPN与故障树分析法[9]很相似,根据已发展成熟的故障树进行FRPN映射建模[10]。
a) 一般地,故障树与petri网之间的转换规则如下:
1) 故障树中的事件可转换为Petri网中的库所;故障树中的基本事件对应petri网中的初始库所,故障树的顶事件对应petri网中的目标库所。
2) 故障树中事件发生的因果关系可转换为Petri网中的变迁;
3) 故障树中的逻辑门,应根据不同含义进行转换,其中与门和或门可以按照图1中所示,转换成Petri网中的符号。特别是故障树中的复合逻辑门,可用若干个基本逻辑门描述。为方便起见,故障树中的复合逻辑门经过简化后再转化为Petri网模型。
b) 故障树中的逻辑门转化为Petri网表示时,运算规则需要同时更新,如图1所示。主要的规则如下:
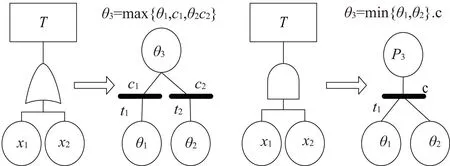
图1 与/或门对应的Petri网表示
1) 如果一个变迁被触发,库所中的托肯将会被送入上一级库所中。
2) 如有变迁结构类似与门结构,上一级库所的真度值由输入库所的最小值真度值确定;如果变迁结构类似或门机构,则上一级库所的真度值由输入库所的最大真度值确定。
1.3FRPN的推理算法
采用一种实用的不确定推理方法,即MYCIN置信度方法[11]来进行正向推理。该方法被广泛的应用与不确定推理,它的主要思路是模糊命题合取式的真值取各子式真值的最小值,模糊命题析取式的真值取各子式真值的最大值。引入极大代数中的两个算子:

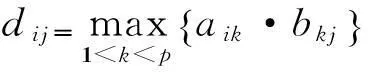
FRPN的推理规则包括使能规则和激发规则[4],为了更好地表示FRPN的推理规则,文中使用了上述运算符计算得到控制向量ρ和激发向量μ。
(1)
其中,采用“neg”算子得到变迁的多个输入库所中托肯的最小值(即对应命题为真的可信度)。
(2)
当一组规则被激发后,FRPN的真度向量和标识向量变为
(3)
由此,可以得到推理算法如下所示:
步骤1,根据FEPN模型得到I,O,H,C,θ0,γ0;
步骤2,令k= 0;
步骤3,根据式(1)~(3),由θk计算得到θk+1;
步骤4,如果θk+1≠θk,令k=k+1,重复步骤3;如果θk+1=θk,推理结束。
2车门系统的故障树模型
地铁车门主要有开门、关门、警示灯/蜂鸣器、障碍物探测(关门防夹、开门时障碍物探测)、车门退出服务、紧急解锁等功能。地铁车辆自动塞拉门系统由门扇、机构和控制系统组成;门扇包括门板、玻璃、胶条和其它零件等;机构包括基础部件、驱动锁闭装置、承载导向装置、内外操作开关等;控制系统包括电子门控器(EDCU)、执行器件、检测器件等。其中承载导向机构由短导柱、挂架、长导柱、携门架、导向滚轮、上下导轨构成;驱动锁闭装置包括车门电机、丝杆螺母副和锁闭装置。车门系统示意图如图2所示。
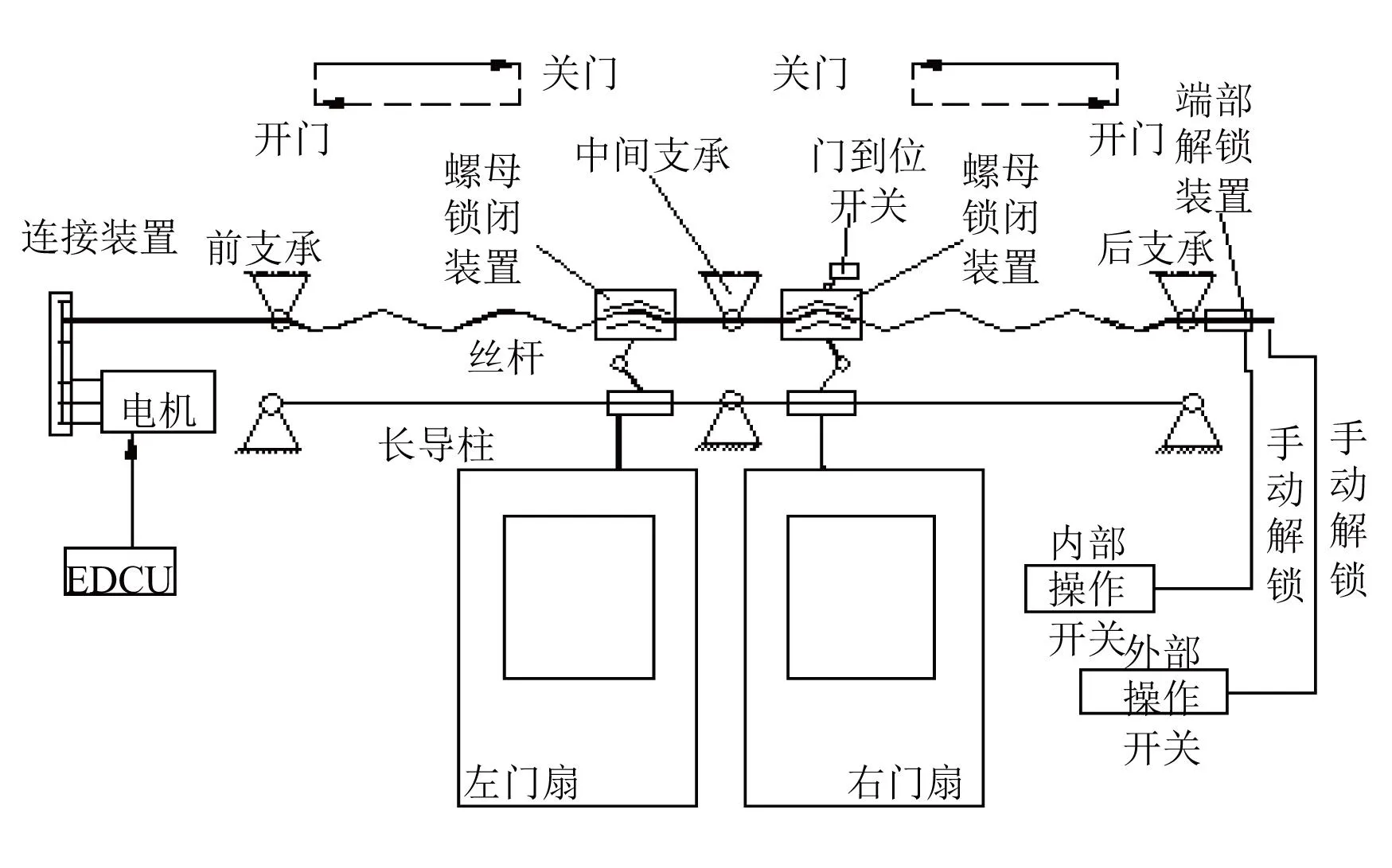
图2 车门系统原理图
车门故障可以分为机械故障和电器故障,通过分析列车运行历史数据可得到,电器故障主要表现为EDCU、车门电机、继电器、限位开关等引起的开、关门问题等;机械故障主要是车门尺寸变形、解锁装置、传动部件卡滞、丝杆螺母磨损开裂、螺丝松动松脱等引起的车门品质减弱问题。
针对车门故障进行详细、系统的分析,通过对影响车门功能的各个中间事件进行分析,逐步分解引起故障的原因,建立车门故障树。图3为车门系统失效故障树,其中标识对应的事件见表1。

图3 地铁车门系统的故障树模型

标识(FTA)标识(FRPN)事件标识(FTA)标识(FRPN)事件TP23地铁车门故障x5P4紧急解锁开关S3y1P20控制系统失效x6P7EDCU内部模块故障y2P12行程开关故障x7P6继电器故障y3P13门控信号错误x8P5ATP故障y4P19驱动系统失效x9P8齿轮组件故障y5P21解锁失效x10P9电机组件故障y6/解锁信号故障x11P10电源故障y7P22机械传动失效x12P14内部操作单元x1P11开/关门按钮故障x13P15解锁组件失效x2P1锁闭开关S1x14P16导轨卡滞x3P2关门行程开关S4x15P17丝杆/螺母副卡滞x4P3隔离开关S2x16P18压轮过紧
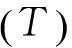
3基于FRPN的车门可靠性分析
3.1车门系统的FRPN模型
车门系统的FRPN模型由上一章节中的故障树模型转换得到,如图4所示。其中的初始库所为P1,P2,P3,P4,P5,P6,P7,P8,P9,P10,P11,P14,P15,P16,P17,P18。其中故障树的事件“解锁信号错误”依据吸收原则[12]在FRPN模型中省略。车门系统FRPN模型包含有23个库所和22个变迁,FRPN模型中库所对应的事件如表1所示。
3.2基于FRPN的车门可靠性分析
对地铁车门系统进行事故诊断,由图4可得该Petri网的输入矩阵I、输出矩阵O、互补矩阵H:


图4 车门系统的FRPN模型
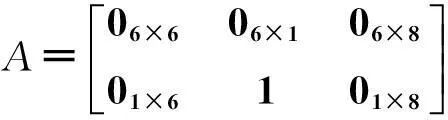

B2=

给定各事件传播关系(规则)的可信度为C22×22=diag(0.9, 0.8, 0.7, 0.7, 0.95, 0.7, 0.9, 0.8, 0.85, 0.7,0.7, 0.85, 0.95, 0.8, 0.7, 0.7, 0.8, 0.75, 0.8, 0.9, 0.85, 0.75)。
则由推理算法得到:
θ1(θi,i=12,13,19,20,21,22,23)=(0.72, 0.81, 0.51, 0.28, 0.42, 0.56, 0)
θ2(θi,i=12,13,19,20,21,22,23)=(0.72, 0.81, 0.51,0.7695, 0.42, 0.56, 0.42)
θ3(θi,i=12,13,19,20,21,22,23)=(0.72, 0.82, 0.51, 0.28, 0.42, 0.56, 0.6925)
θ4(θi,i=12,13,19,20,21,22,23)=(0.72, 0.82, 0.51, 0.28, 0.42, 0.56, 0.6925)
由于θ4=θ3,推理过程结束。在初始条件θ0下,系统真度值为θ4(θi,i=12,13,19,20,21,22,23)=(0.72, 0.82, 0.51, 0.28, 0.42, 0.56, 0.6925)。则系统目标事件发生的最大可信度为0.69255。
为了评估基本事件对系统整体性能的影响,定义当只有一个故障发生时,通过FRPN推理算法计算得到的目标事件的真度值为基本事件重要度指标Iotd。底事件重要度计算结果如表2所示。计算结果表明,p7,p1,p2,p17的重要度值最大,表明事件“EDCU模块故障”、“锁闭开关S1故障”、“关门到位开关S4故障”、“丝杆/螺母副卡滞”是最重要的事件。由于初始库所的重要度指标值越大,对系统性能的影响就越严重,工程人员可依据计算结果制定维修策略,加强对这些薄弱环节的维护。
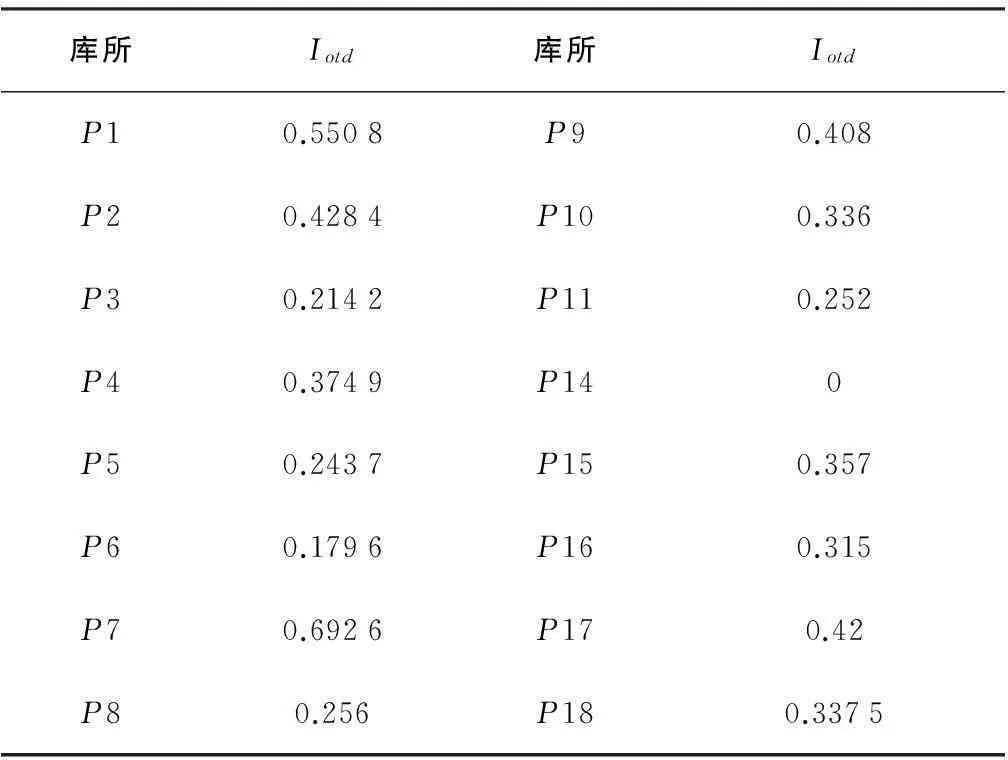
表2 初始库所的重要度指标
5结语
文中研究地铁车门系统的可靠性,首先建立车门系统故障树模型,然后通过FTA-FRPN的图形转化规则得到Petri网模型,最后将模糊推理Petri网的推理算法应用于车门系统整体的可靠性分析,计算得到目标事件的故障率和初始事件的重要度。计算结果展示了影响车门运行性能的故障排序,有助于技术人员和维修人员分析车门系统的运营状况,并且通过采用恰当的维修策略提高系统性能。其有效的模糊推理过程及智能推理能力便于计算机编程求解复杂过程。
参考文献:
[1] 朱小娟,王建兵,印臻民. 上海地铁车辆客室车门可靠性技术研究[J]. 城市轨道交通研究,2006,(3):31-34.
[2] 周俊龙,王建兵. 上海地铁车辆客室车门可靠性和安全性技术研究[J]. 电力机车与城轨车辆, 2006,29(4):7-10.
[3] Zhou Liming, Yang Jianwei, Cai Guoqiang. Monte-Carlo Simulation Based on FTA in Reliability Analysis of Door System[J]. ICCAE,2010. The 2nd International Conference on (Volume:5 ) 26-28 Feb, 2010 page(s):713-717.
[4] Wu Jianing, Yan Shaoze, Xie Liyang. Reliability analysis method of a solar array by using fault tree analysis and fuzzy reasoning Petri net[J]. Acta Astronautica. 2011,(69) 960-968.
[5] 刘心,印桂生,张磊. 基于FRPN的水下机器人故障诊断[J]. 计算机工程与应用, 2010, 46(19): 217-219.
[6] 高梅梅,吴智铭. 模糊推理Petri网及其在故障诊断中的应用[J]. 自动化学报, 2009, 26(5): 677-680.
[7] 陈茹雯. 基于广义随机Petri网的轨道车辆门系统可靠性分析[J]. 科学技术与工程, 2013, 13(4): 1095-1098.
[8] 马小平, 李明, 鲍海勇. 基于模糊推理Petri 网的胶带运输系统故障诊断[J]. 东南大学学报, 2003, 33(sup): 127-129.
[9] 全达,孙秀芳,王缅. 基于故障树分析法的识别单元可靠性分析[J]. 现代制造工程, 2012, 4 : 122-125,93.
[10] 黄光球,朱华平,郑彦全. 基于模糊Petri网的事故树模糊分析方法研究[J]. 湖南科技大学学报, 2006, 21(2):34-39.
[11] Lu Qiuqin, Huang Guangqiu. Fuzzy Analysis of Accidents Diagnosis Based on Fuzzy Petri Net[J]. International Journal of Systems and Control, 2007, 2(3): 228-236.
[12] 张永发,蔡琦,赵新文. 一种基于Petri网模型进行故障树分析的改进算法[J]. 强度与环境, 2007, 34(6): 51-56.
欢迎投稿欢迎刊登广告欢迎订阅
Reliability Analysis of Metro Door System Using FTA and Fuzzy Reasoning Petri Net
LIU Guang-wu1, CAI Chang-jun1, CHEN Gang1, YANG Ling-zhi1, XING Zong-yi2
(1. Guangzhou Metro Corporation, Guangzhou 510030, China;
2. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China)
Abstract:In order to carry out door system reliability analysis, a methodology involving qualitative modeling using FTA and quantitative analysis using FRPN method is proposed in this paper. The fault tree model of the door system is established on the basis of analyzing the door system and cause. and-effect relationship of events, the FRPN model is converted from a fault tree model to through graphical transformation rules; and then, the reasoning algorithm is used in door system reliability analysis, and the failure rate of target event and the importance and sorting of initial events are calculated. The results are helpful to the technical personnel and maintenance personnel for analyzing the systems’ behavior.
Keywords:reliability analysis; sliding plug door; FTA; fuzzy Petri net
基金项目:国家自然科学基金(51175262);江苏省产学研前瞻项目(SBY201220116);江苏省杰出青年基金(SBK201210111)
收稿日期:2014-12-09
中图分类号:U231;TB114.3
文献标志码:A
文章编号:1671-5276(2015)03-0146-04
作者简介:刘光武(1956-),男,广东广州人,高级工程师,从事城市轨道交通运输系统研究。
