灰色模型在疲劳寿命预测中的应用
2015-12-28王海山刘峰曹燕龙陈金池
王海山,刘峰,曹燕龙,陈金池
(辽宁石油化工大学,辽宁 抚顺 113001)
灰色模型在疲劳寿命预测中的应用
王海山,刘峰,曹燕龙,陈金池
(辽宁石油化工大学,辽宁 抚顺 113001)
摘要:疲劳寿命预测的问题是疲劳研究中的重要课题。影响疲劳寿命的因素多且复杂,利用灰色理论方法进行疲劳寿命预测,提出了非等间距GM(1,1)模型和中心逼近式GM(1,1)模型两种预测疲劳寿命的方法。通过对实验数据进行分析和整理,然后建立微分方程,利用MATLAB软件计算得到灰色预测值。与实验数据值进行比较,得出结果表明灰色模型方法具有很高的预测精度,证明灰色理论是一种简单可行的、可靠的分析方法。
关键词:疲劳寿命;灰色理论;非等间距GM(1,1)模型;中心逼近式GM(1,1)模型
0引言
材料的疲劳是指材料在循环载荷作用下所发生的性能的变化。美国ASTM对疲劳定义为:在某点或某些点承受足够多的循环扰动之后,形成裂纹或者完全断裂的材料中所发生的局部性、永久性的结构变化的发展过程[1]。因为影响疲劳寿命的因素众多,并且某些因素对疲劳寿命的影响是未知或不确定的[2],所以准确预测疲劳寿命十分困难,这是疲劳寿命问题没有得到解决的原因。目前,预测材料疲劳寿命的方法很多,但是很多是建立在确定性理论的基础上的,由于实验数据的缺乏而无法预测。然而,灰色理论把疲劳现象看作一个小样本、贫信息的不确定性系统,所需要的实验数据少,真实地反映了疲劳现象的客观规律,为疲劳寿命的预测提供了一种新的方法[3]。
1灰色系统理论的基本原理
灰色系统是指即含有已知信息、又含有未知信息的系统,也称为贫信息系统。灰色系统理论中,称抽象系统的逆过程为灰色模型,亦称GM,通常GM表示为GM(n,h),当n=h=1时可以表示为单变量一阶灰色预测模型[4]。灰色预测将一组信息不完全、具有很大随机性的原始数据进行m次累加处理后,利用这些信息,建立灰色预测模型,从而确定系统未来的变化趋势[5]。在所建模型中,单数列微分模型GM(1,1) 由于具有较好的拟合性与外推特性[6],比较适合于可靠性分析中的疲劳寿命预测。
文中主要用非等间距GM(1,1)模型和中心逼近式灰色GM(1,1)模型两种方法进行疲劳寿命预测,以及两种方法得出结果的精确性比较。
2非等间距GM(1,1)模型
在实际的工作和试验中得到的数据并不都是等间距或者有规律性的,而初始的GM(1,1)模型却要求建模的数据序列必须是等间距的,所以,需要得到一组等间距的数据序列才能完成建模。这样做就不可避免的产生随机误差,致使建模的精度降低。因此,利用非等间距GM(1,1)模型可以解决等间距数据处理带来的误差,用此方法找出非等间距数据间的内在联系,从而可以进行数据预测。
2.1建立非等间距GM(1,1)模型
设初始序列为[7]:
X(0)(σ)={x(0)(σ1),x(0)(σ2),…,x(0)(σn)}Δσk=σk-σk-1≠c,c为常数。称X(0)(σ)为非等间距序列。
X(1)(σ)={x(1)(σ1),x(1)(σ2),…,x(1)(σn)}为X(0)(σ)的一次累加(1-AGO)序列。
Z(1)(σ)={z(1)(σ1),z(1)(σ1),…,z(1)(σn)}为X(0)(σ)的紧邻均值序列,
(1)
由此可以将GM(1,1)模型的表达式X(0)(σ)+aZ(1)(σ)=u转化为:
X(0)(σk)+aZ(1)(σk)Δσk=uΔσk
(2)
式(2)称为灰色模型。
式中:Δσk=σk-σk-1,a和u是模型参数。此时模型的白化方程为:
(3)
式(3)求解得:
X(1)(σ)=[x(0)(σ1)-u/a]e-a(σ-σ1)+u/a
(4)
同时得到非等间距GM(1,1)模型的响应式为:
(5)
其中:

(6)

(7)
2.2实例分析
从文献[8] 的弯曲实验的S-N曲线(图1)中采集到41Cr4材料的疲劳寿命随应力变化的数据(表1)。

表1 疲劳寿命随应力变化的关系

图1 S-N曲线
将原始数据处理x(0)(σi)=Ni/106得:
X(0)(σ)={0.87,0.155,0.047,0.021,0.0116,0.009}
Z(1)(σ)={0.9475,1.0485,1.0825,1.0988,1.1091}
Δσk={7.5,7.5,6.1,5.2,2.5}
将上面的数据代入式(6)和式(7),用MATLAB软件计算得:
即a=-0.1247,u=0.1383。
取x(0)(21.2)=0.87,可以得到非等间距GM(1,1)模型的时间响应为式(8):
(8)
将σk和Δσk的值代入式(8)中可以得到不同应力下的疲劳寿命预测值。预测值与实验数据的比较如表2。
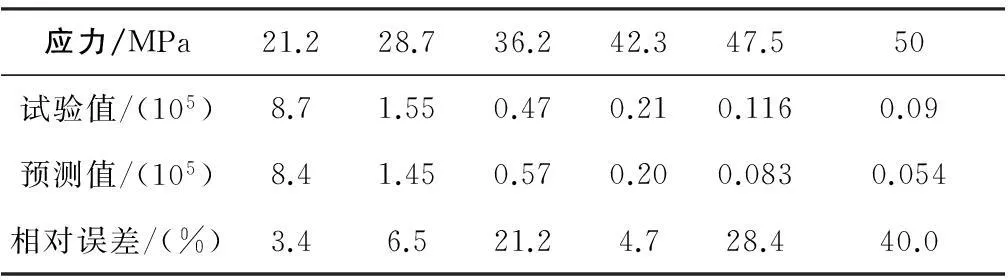
表2 预测值与实验数据的比较
由表2中的结果可以得出平均误差为104.4%/6=17.4%,按照误差等级评价17.4%<35%属于好的等级范围。为了更好的说明模型具有很高的拟合性,把寿命预测数据与试验数据用origin软件绘制如图2。

图2 试验寿命曲线与预测寿命曲线
从图2中可以看出,在预测寿命曲线上中间点处与曲线总体走势不符合,原因可能是由于试验条件的改变导致误差的产生。虽然两条曲线在一些地方偏离较大,但是总体的拟合性还是很好的,说明非等间距GM(1,1)模型建模精度较高,对于非等间距序列的建模是非常实用和有效的[9]。
3中心逼近式灰色GM(1,1)模型
中心逼近式灰色GM(1,1)模型是针对等间距序列建模的。方法以及求解过程如下:
设x(0)={x(0)(1),x(0)(2),…,x(0)(n)}为正离散点列,一次累加后的序列为:
x(1)={x(1)(1),x(1)(2),…,x(1)(n)}
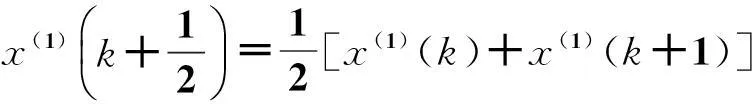

图3 曲线斜率与导数的关系
设一系统x(t)=aeut,则:
x(k+1)-x(k)=aeku(eu-1)
当u→0时,上面两式子的右端接近,也可以说,当x(t)变化不大时,以x(k+1)与x(k)的差作为t=k+1/2时刻的导数更加合理。
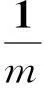
其中离散形式的时间相应式为:
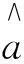
式中:
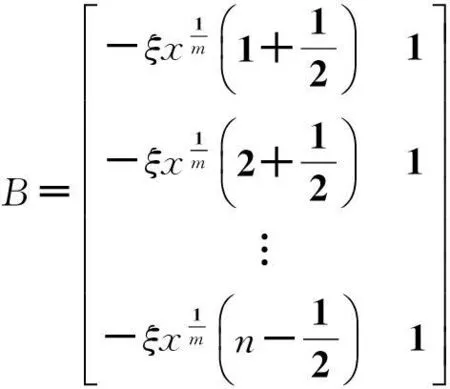
(9)
(10)
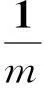
3.1实例分析
由于中心逼近式灰色GM(1,1)模型需要的数据是等间距的,所以从图1的S-N曲线及表1的数据组中选择等间距的4个应力22MPa,20MPa,18MPa,16MPa所对应的疲劳寿命8.2×105,10.9×105,15.2×105,23.1×105作为原始序列。求解如下:
x(0)=(8.2,10.9,15.2,23.1)作为原始序列,对此取m=2,且x(0)呈现指数规律,对x(0)直接建模,
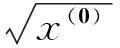
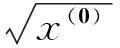
把上面数据代入式(7),式(8)得:

用MATLAB软件计算得[a,u]T=[-0.3730,-0.7243]T,
即a=-0.3730,u=-0.7243。
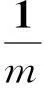
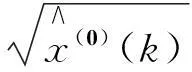
(11)
将K=1,2,3,···,n,代入平方得x(0)的预测值与实验数据的比较如表3所示。
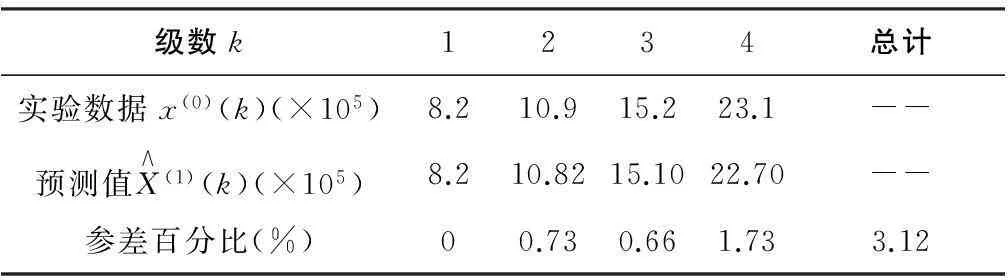
表3 预测值与实验数据的比较
平均误差为3.12%/4=0.78%,预测精度p=1-0.78%=99.22%。将k=5,6,···,代入式(11)得,即为14MPa,12MPa,···,的疲劳寿命预测值[9]。
4结果与讨论
两种灰色建模方法的预测结果及精度比较见表4。

表4 两种建模方法精度比较
从表4中数据可以看出非等间距GM(1,1)模型的预测精度小于中心逼近式GM(1,1)模型的预测精度。说明中心逼近式GM(1,1)模型精确度更高,预测效果更好。但是非等间距GM(1,1)模型的使用范围很广,操作简便,数据预测没有局限性。而中心逼近式GM(1,1)模型需要取等间距的序列,就带来了数据取值的局限性,同时数据预测也具有局限性,这样就造成中心逼近式GM(1,1)模型的使用性降低。
5结论
疲劳现象是一个发展变化受众多因素影响的复杂过程,文中视疲劳问题为一个灰色系统,提出了非等间距GM(1,1)模型和中心逼近式GM(1,1)模型两种预测疲劳寿命的方法。通过建立微分方程,求解预测出的实验数据,然后与实际数据进行比较得到预测值具有很高的精度,这是传统的疲劳寿命预测方法无法做到的。与一般的试验数据处理方法相比,灰色系统理论中的灰色模型不仅需要的数据少,而且还避开了复杂繁琐的模型建立,操作简单实用性强。并且两种灰色模型具有良好的通用性与准确性,为准确地确定疲劳寿命值提供了一种实用的分析方法。
参考文献:
[1] 雷冬. 疲劳寿命预测若干方法的研究[D]. 合肥:中国科学技术大学博士论文,2006:01-03.
[2] 姚卫星. 结构疲劳寿命分析[M]. 北京:国防工业出版社,2003.
[3] 孙玉兰,王茂廷. 基于灰色模型GM(1,1)的疲劳寿命预测[J]. 科学技术与工程,2011,11(3):560-562.
[4] 刘思峰,等. 灰色系统理论及其应用[M]. 北京:科学出版社,1999.
[5] 熊和金,徐华中. 灰色控制[M]. 北京:国防工业出版社,2005.
[6] 徐春龙,徐元利,等. 灰色系统理论在内燃机疲劳寿命预测中的应用[J]. 车用发动机,2011,131(1):23-25.
[7] 邓聚龙. 灰理论基础[M]. 武汉:华中科技大学出版社, 2002.
[8] 郦明,奥脱·布克斯鲍姆. 结构抗疲劳设计[M]. 北京:机械工业出版社,1987.
[9] 史雪荣,王作雷,张正娣. 变参数非等间距GM(1,1)模型及应用[J]. 数学的实践与认识,2006,36(6):216-220.
Application of Gray Model in Fatigue Life Forecast
WANG Hai-shan, LIU Feng, CAO Yan-long, CHEN Jin-chi
(Liaoning Shihua University, Fushun 113001, China)
Abstract:Forecasting fatigue flife is an important issue in the study of fatigue. The factors that affect the fatigue life are complex and uncertain. By using gray theory, the non-equidistance GM (1, 1) model and center approach gray GM (1, 1) model are proposed in this article, which are used to forecast the fatigue life. After analysing experimental data and building differential equation, MATLAB software is used to calculate the gray forecast. Compared with the experimental data, it comes to conclusion that the prediction accuracy is very high and it is proved that the gray theory is a simple and feasible approach.
Keywords:fatigue life; gray theory; non-equidistance GM (1, 1) model; center approximation type GM (1, 1) model
收稿日期:2014-12-09
中图分类号:TH123+.1
文献标志码:B
文章编号:1671-5276(2015)03-0123-04
作者简介:王海山(1987-),男,硕士研究生,研究方向:材料疲劳寿命预测。
