PTW整环的t-全变换与t-平坦扩环
2015-12-28万吉湘,徐龙玉
PTW整环的t-全变换与t-平坦扩环
万吉湘1,徐龙玉2
(1.绵阳师范学院数学与计算机科学学院,四川绵阳621000;2.西南科技大学理学院,四川绵阳621010)
摘要:利用素理想在星型算子研究中的特殊性,引入t-全变换的概念,对PTW整环进行了讨论,证明了R是PTW的SM整环,则Rtg=K.给出了PTW整环与其t-平坦扩环也是PTW整环的等价描述,进一步对PTW整环进行了探讨.
关键词:PTW整环; t-全变换;t-平坦扩环
收稿日期:2015-05-20
基金项目:绵阳师范学院2014年度自然科学重点项目“乘法理想理论中的Gorenstein同调法”(2014A04)
作者简介:万吉湘(1981—),女,四川泸州人.讲师,主要从事交换代数与同调代数研究.
中图分类号:O153.3文献标志码:A
本文恒设R是整环,K为其商域,R的扩环T是指T为R-模,且R⊆T⊆K.对于K中的任意R模A,令
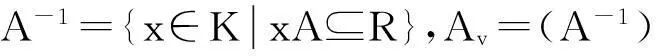
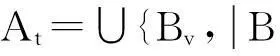
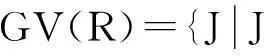
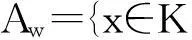
F(R)上的映射I→I,I→Iv,I→It,I→Iw分别称为R的d-,v-,t-,w-算子.
在前人的研究中,素理想的特殊性在星型算子的研究中没有得到体现.2006年,文[1-3]中提出了PTW整环的概念,即R是PTW整环当且仅当R的任何素w-理想是t-理想,并说明了PTW是TW整环的推广.本文在此基础上对PTW整环做进一步的研究,讨论PTW整环R与其t-全变换、t-平坦扩环之间的关系.
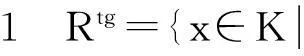
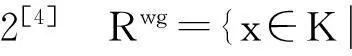
定义3[5]所谓t-平坦扩环T是指T是整环R的扩环,且对T中任意极大t-理想Q,TQ=RQ∩R.
在[5]中指出T是R的t-平坦扩环当且仅当存在广义乘法集Σ,使得T=RΣ,且对任意A∈Σ,(AT)t1=T.
定理1若R是Mori整环,则Rwg不是平坦R-模.
证明:R是Mori整环,由[4],Rwg是Mori整环.对R中任意极大w-理想A,我们说(ARwg)-1=Rwg.事实上,Rwg⊆(ARwg)-1显然.现证(ARwg)-1⊆Rwg.令x∈(ARwg)-1,则xARwg⊆Rwg,从而xA⊆Rwg.由R是Mori整环,存在有限生成理想B⊆A,使得Bv=Av,故xB⊆Rwg.由于B有限生成,故存在极大w-理想C1,…,Cn,使得xAC1…Cn⊆xAvC1…Cn=xBvC1…Cn⊆(xBC1…Cn)v⊆R.从而x∈Rwg.故Rwg=(ARwg)-1.
若Rwg是平坦R-模,A为R的极大w-理想,从而是t-理想,则ARwg是Rwg的t-理想.下面我们证ARwg是极大w-理想.若否,则存在Rwg的极大w-理想Q,使得ARwg⊆Q,从而Qv1=Rwg.Rwg是Mori整环,则Q是v-理想,故矛盾.因此ARwg是极大w-理想,从而与(ARwg)-1=Rwg矛盾.故Rwg不是平坦R-模.
注:根据定理1进一步设R是SM整环,R是PTW整环当且仅当若扩环T是平坦R-模,且T⊂Rwg,则T是PTW整环.
证明:由定义3即得.
定理2Rtg是R的w-扩环.
证明:令x∈(Rtg)w,则存在J∈GV(R),使得Jx⊆Rtg.J有限生成,于是存在素t-理想M1,…,Mk,使得M1…MkJx⊆R.由Jw=R,我们有M1…Mkx⊆(M1…Mkx)w⊆R.故x∈Rtg,从而Rtg=(Rtg)w,Rtg是R的w-扩环.
引理1[6]设R是SM整环,I是R的w-理想,则I上只有有限个极小素理想,且都可以表示为(I:x),其中x∈R-I.
定理3R是PTW的SM整环,则Rtg=K.
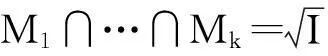
((M1…Mk)n)w=((I1…Ik)n)w⊆Iw=I,
因此(M1…Mk)n⊆I=(R:x),x∈Rtg,从而Rtg=K.
推论2R是SM整环,w-dim(R)=1,则Rtg=K.
定理4R为v-凝聚整环,则以下等价.
(1) R是PTW整环.
(2)若t-平坦扩环T为v-凝聚整环,则T也是PTW整环.
(3)若t-平坦扩环T是平坦R-模,则T是PTW整环.
证明:根据定理3以及t-平坦扩环的定义即可证得.
参考文献:
[1] 万吉湘, 王芳贵.PTW整环的刻画[J].四川师范大学学报:自然科学版, 2006(4):392-396 .
[2] 万吉湘, 王芳贵. PT整环的研究[J].四川师范大学学报:自然科学版, 2010(1):27-31.
[3] 万吉湘, 王芳贵. 关于PTW整环的多项式环[J].绵阳师范学院学报:自然科学版, 2010(11):15-17 .
[4] M.H.Park.OnoverringsofStrongMoridomains[J].Pure. Appl.Algebra, 2002(1):79-85.
[5] D.J.Kwak,Y.S.Park.Ont-flatoverrings[J].Chinese Journal of Mathematics, 1995(1) :17-24.
[6] Wang Fanggui, R.L.McCasland.OnStrongMoridomains[J].J.Pure.Appl.Algebra, 1999(6):155-165.
[责任编辑范藻]
The t-global Transform and t-flat Overring of PTW Domain
WAN Jixiang1,XU Longyu2
(1. Mathematics and Computer Science School of Mianyang Normal University, Mianyang Sichuan 621000;
2. Science College of Southwest University of Science and Technology, Mianyang Sichuan 621010, China)
Abstract:In this paper, by the particularity of prime ideal in study of star operator, the concept of t-global transform is imported to further discuss PTW domain. We prove that if R is SM domain of PTW, then Rtg=K. Moreover, we show when a ring is PTW domain if and only if its t-flat overring is also PTW domain. So the theories about PTW domain are enriched consumedly.
Key words:PTW domain; t-global transform; t-flat overring
