支撑形式对钢弹簧浮置板轨道减振性能的影响
2015-12-28刘维宁彭智勇
金 浩,刘维宁,赵 磊,马 蒙,彭智勇
(1.绍兴文理学院 土木工程学院,浙江 绍兴 312000;2.北京交通大学 土木建筑工程学院,北京 100044;3.中国铁道科学研究院 铁道建筑研究所,北京 100081)
支撑形式对钢弹簧浮置板轨道减振性能的影响
金 浩1,刘维宁2,赵 磊2,马 蒙3,彭智勇2
(1.绍兴文理学院 土木工程学院,浙江 绍兴 312000;2.北京交通大学 土木建筑工程学院,北京 100044;3.中国铁道科学研究院 铁道建筑研究所,北京 100081)
为了改善钢弹簧浮置板轨道的减振性能,以现有液压弹簧阻尼器的布置形式为基础,设计了一种全新的液压弹簧阻尼器布置形式。利用ABAQUS数值模拟软件建立显式计算有限元模型,施加现场实测的定点轮轨力。通过MATLAB编程软件;分析两种布置形式下,轨道板和基底的振动加速度时程、三分之一倍频程以及Z振级。结果表明在列车轮轨力作用下,现有钢弹簧浮置板轨道的轨道板振动幅值大于新型钢弹簧浮置板轨道;同时,基底振动加速度三分之一倍频程和Z振级分析都证实了在低频区,新型钢弹簧浮置板轨道具有更好的减振效果。
振动与波;钢弹簧浮置板;时程分析;Z振级
近几年,随着我国城市轨道交通的大量投入运营,由轮轨耦合振动引起的环境振动问题日益突出。具有完善减振措施的钢弹簧浮置板轨道,相比于其它轨道减振型式[1,2],从进入中国轨道交通市场起,在地铁减振方面一直发挥着重要作用。
目前,对于钢弹簧浮置板轨道的研究,大致可归纳为理论解析分析、数值模拟分析(自编程序或者商业软件)以及测试分析(实验室或者现场)。2006年,郭亚娟等[3]利用ANSYS软件,建立了浮置板轨道系统的有限元模型。采用Newmark时间积分方法,模拟了列车荷载作用下,浮置板轨道结构的瞬态响应。2008年,丁德云等[4]应用MIDAS/GTS软件,对浮置板轨道进行了三维模态分析。2009年,谷爱军等[5]建立了三维钢弹簧浮置板轨道有限元模型,针对不同设计参数和激振频率,研究了该轨道结构的动力传递特性和隔振效率。2011年,丁德云等[6]采用MIDAS/GTS软件对钢弹簧浮置板轨道进行了动力特性研究。刘维宁等[7]利用“北京交通大学轨道减振与振动控制试验室”进行了钢弹簧浮置板轨道低频特征测试,研究了钢弹簧浮置板轨道弹簧刚度和支承间距等参数变化对低频振动的影响,并比较了钢弹簧浮置板轨道和普通轨道的低频减振效果。2012年,肖安鑫等[8]通过不同钢弹簧浮置板轨道地段车内噪声的对比测试,分析了钢弹簧浮置板轨道对车内噪声的影响。韦红亮等[9]分别采用有限元和现场试验方法,从时频域角度对高架钢弹簧浮置板轨道结构的减振特性进行了分析。2013年,蒋崇达等[10]利用ANSYS软件建立了钢弹簧浮置板轨道系统的双层梁动力学模型,通过瞬态分析模拟了列车移动荷载通过钢弹簧浮置板轨道时的动力响应。
在以上研究的基础上,本文探讨了一种全新的液压弹簧阻尼器布置形式。通过时程分析、1/3倍频程分析以及Z振级分析,比较了新型液压弹簧阻尼器布置形式对钢弹簧浮置板轨道振动特性的影响。
1 液压弹簧阻尼器位置
现有钢弹簧浮置板(以下简称SSFS-1)板长6.0 m,截面为3.5 m×0.45 m,液压弹簧阻尼器设置在浮置板两侧,相邻间距1.2 m,如图1所示。

图1 SSFS-1结构尺寸及液压弹簧阻尼器位置
在现有液压弹簧阻尼器布置形式的基础上,设计了另外一种液压弹簧阻尼器布置形式。将图1(a)中的液压弹簧阻尼器#2、#4、#7、#9去掉,在对应横断面中部设置液压弹簧阻尼器#N2和#N4。新型液压弹簧阻尼器布置形式的钢弹簧浮置板轨道(以下简称SSFS-2)如图2所示。
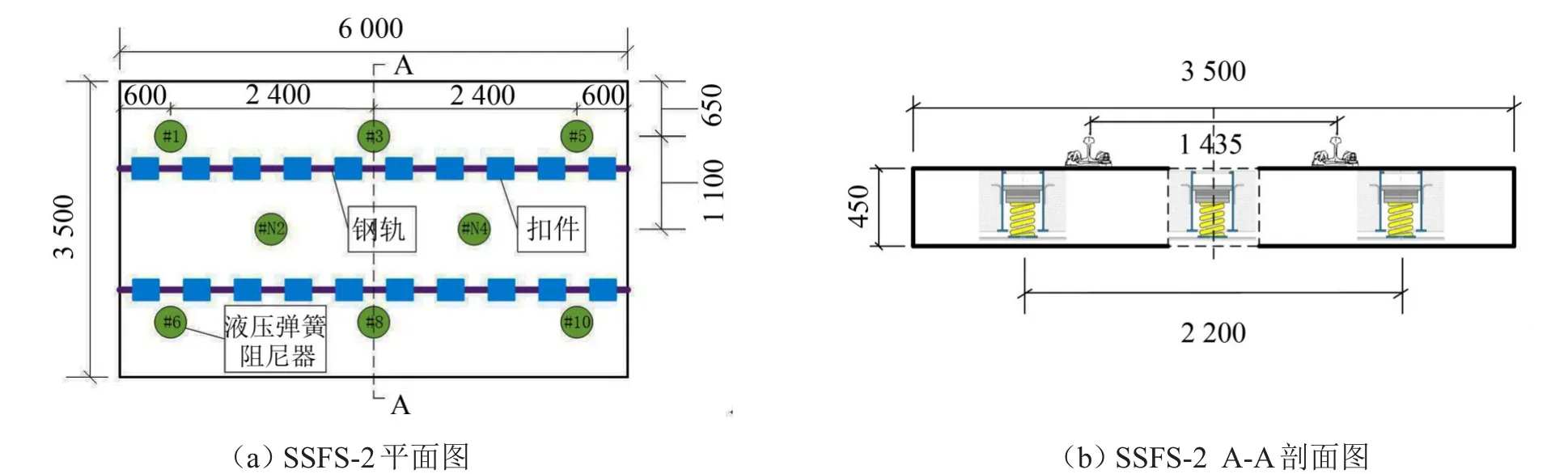
图2 SSFS-2结构尺寸及液压弹簧阻尼器位置
2 数值模型
为了提高网格划分的质量以及减少计算单元数,将钢轨截面简化为工字型截面。钢轨长6.0 m,密度为7 850 kg/m3,弹性模量为2.14×1011N/m2,泊松比为0.3。
扣件和液压弹簧阻尼器的位置如图1和图2所示,用线性弹簧进行模拟。扣件竖向刚度60 MN/m,液压弹簧阻尼器竖向刚度选用5.3 MN/m[4,6]。
浮置板的尺寸如图1和图2所示,密度为2 500 kg/m3,弹性模量为3.1×1010N/m2,泊松比为0.2。基底尺寸6.0 m×5.0 m×0.3 m,密度为2 600 kg/m3,弹性模量为3.6×1010N/m2,泊松比为0.167。典型的有限元模型(SSFS-1)如图3所示。
通过现场测试,得到定点轮轨力(如图4所示)。为了模拟轮对同时施加荷载于左右钢轨上,将测试得到的荷载同时施加在左右钢轨中部,如图3所示。在浮置板中部和基底边缘处(如图3所示),设置振动加速度拾振点。考虑到主要关心频率是1 Hz~200 Hz,将拾振点采样频率设置为500 Hz(即采样点间隔时间0.002 s)。
3 结果分析
3.1 时程分析
浮置板和基底拾振点采样时长设置为15 s,得到SSFS-1和SSFS-2的浮置板振动加速度时程和基底振动加速度时程,如图5和图6所示。

图3 SSFS-1有限元模型
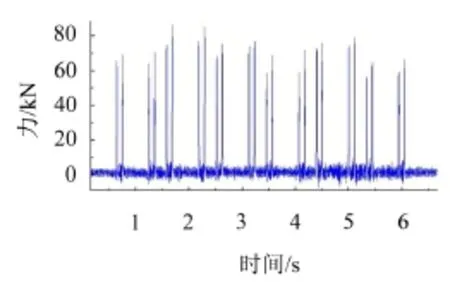
图4 轮轨力时程
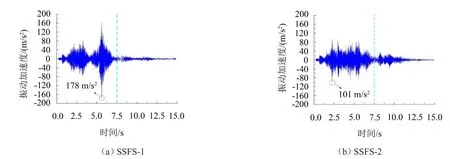
图5 浮置板振动加速度时程
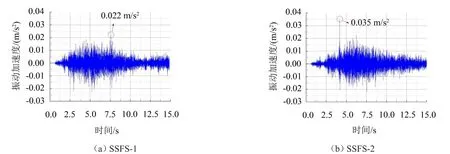
图6 基底振动加速度时程
比较SSFS-1和SSFS-2的浮置板振动加速度时程,得到:
(1)SSFS-1的浮置板振动加速度最大值为178 m/s2,SSFS-2的浮置板振动加速度最大值为101 m/s2;
(2)以时间历程7.5 s为参考线,发现SSFS-1的浮置板振动加速度衰减比SSFS-2快。
比较SSFS-1和SSFS-2的基底振动加速度时程,得到:SSFS-1的基底振动加速度最大值为0.022 m/ s2,SSFS-2的基底振动加速度最大值为0.025 m/s2。
3.2 1/3倍频程分析
将测试得到的时程数据,利用MATLAB软件,进行FFT变换,得到SSFS-1和SSFS-2的浮置板和基底振动加速度频谱。然后通过频域数据处理方法,得到1/3倍频程,如图7和图8所示。
比较SSFS-1和SSFS-2的浮置板振动加速度1/3倍频程,得到:SSFS-1的浮置板振动加速度最大值发生在中心频率40 Hz频段,对应幅值为138.9 dB;SSFS-2的浮置板振动加速度最大值也发生在中心频率40 Hz频段,对应幅值为137 dB。
比较SSFS-1和SSFS-2的基底振动加速度1/3倍频程,得到:
(1)对于浮置板的自振频率,从图8(a)和图8(b)可以看出,SSFS-2的1阶自振频率低于SSFS-1的一阶自振频率;
(2)图8(c)为SSFS-1和SSFS-2的基底振动加速度1/3倍频程比较,从图上可以看出,SSFS-1和SSFS-2的基底振动加速度在25 Hz以上相差不大,主要差别在1 Hz~25 Hz低频区。1 Hz~25 Hz低频区,SSFS-2的基底振动加速度级普遍小于SSFS-1。

图7 浮置板振动加速度1/3倍频程

图8 基底振动加速度1/3倍频程
3.3 Z振级分析
分析基底振动加速度Z振级,分析频段取1 Hz~80 Hz,采用ISO 2631-1:1997计权网络,如表1所示。得到:1 Hz~80 Hz频段,SSFS-1的Z振级为57.1 dB,SSFS-2的Z振级为56.4 dB。
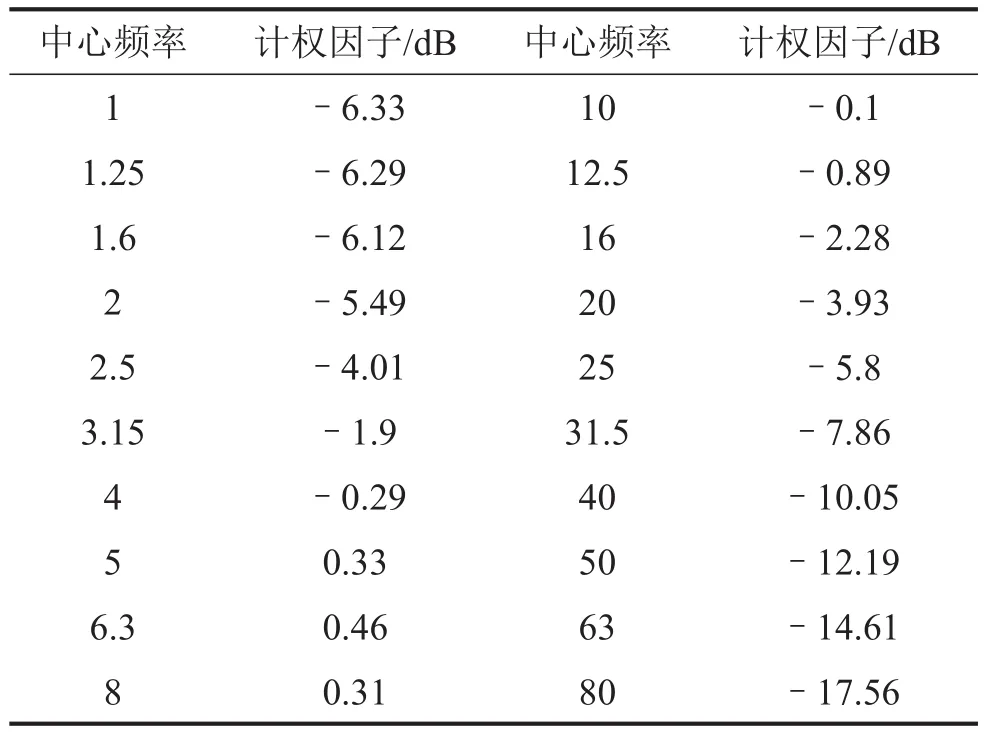
表1 ISO 2631-1:1997计权因子
4 结语
本文在现有液压弹簧阻尼器布置形式基础上,设计了一种全新的液压弹簧阻尼器布置形式。通过时程分析、1/3倍频程分析以及Z振级分析,得出如下结论:
(1)列车轮轨力作用下,现有钢弹簧浮置板轨道的轨道板振动幅值大于新型钢弹簧浮置板轨道;
(2)基底振动加速度1/3倍频程和Z振级都表明,在低频区,新型钢弹簧浮置板轨道具有更好的减振效果。
[1]金浩,刘维宁,王文斌.梯式轨枕轨道模态试验分析[J].工程力学,2013,30(3):459-463.
[2]金 浩,刘维宁.蚁群算法耦合LS-DYNA梯式轨枕轨道动力特性优化[J].振动与冲击,2013,32(2):24-28.
[3]郭亚娟,杨绍普,郭文武.钢弹簧浮置板轨道结构的动力特性分析[J].振动、测试与诊断,2006,26(2):146-150.
[4]丁德云,刘维宁,张宝才,等.浮置板轨道的模态分析[J].铁道学报,2008,30(3):61-64.
[5]谷爱军,张宏亮.钢弹簧浮置板轨道结构在不同频段的隔振效率[J].噪声与振动控制,2009,29(1):39-42.
[6]丁德云,刘维宁,李克飞,等.钢弹簧浮置板轨道参数研究[J].中国铁道科学,2011,32(1):30-35.
[7]刘维宁,丁德云,李克飞,等.钢弹簧浮置板轨道低频特征试验研究[J].土木工程学报,2011,44(8):118-125.
[8]肖安鑫,田野.钢弹簧浮置板轨道对车内噪声影响的实测与分析[J].噪声与振动控制,2012,32(1):51-54.
[9]韦红亮,练松良,周宇.高架钢弹簧浮置板轨道减振特性分析[J].同济大学学报(自然科学版),2012,40(9):1342-1348.
[10]蒋崇达,雷晓燕.城市轨道交通钢弹簧浮置板轨道动力特性分析[J].城市轨道交通研究,2013,16(3):34-41.
Study on Vibration Reduction Characteristics of the Steel-spring Floating Slab TracksAffected by Different Supporting Forms
JIN Hao1,LIU Wei-ning2,ZHAO Lei2,MA Meng3,PENG Zhi-yong2
(1.College of Civil Engineering,Shaoxing University,Shaoxing 312000,Zhejiang China; 2.School of Civil Engineering,Beijing Jiaotong University,Beijing 100044,China; 3.Railway Engineering Research Institute,ChinaAcademy of Railway Sciences,Beijing 100081,China)
:In order to improve vibration reduction ability of steel-spring floating slab tracks,a new supporting form with hydraulic spring dampers was proposed and studied.A finite element model with explicit algorithm was built using Abaqus software for the floating slab track.The in-situ tested rail-wheel contact force was applied to the model.The time history of vibration acceleration,1/3 octave and Z vibration level of the floating slab and the foundation were analyzed by Matlab for original supporting form and the new supporting form respectively.Results show that:(1)the vibration amplitude of the floating slab of the steel-spring floating slab track with original supporting form is higher than that of the slab track with the new supporting form;(2)in low frequency range,the floating slab track with new supporting form has better vibration reduction ability than that of the slab track with the original supporting form according to the analysis of the 1/3 octave and Z vibration level of the foundation.
:vibration and wave;steel-spring floating slab tracks;time-history analysis;Z vibration level
TB53;U231
:A
10.3969/j.issn.1006-1335.2015.01.008
1006-1355(2015)01-0038-04
2014-06-25
国家自然科学基金项目(51278043)
金浩(1986-),男,浙江诸暨人,讲师,博士,从事轨道振动控制研究。(E-mail:zhujijinhao@gmail.com)
