几何学中的珍宝

陈世亨

一、 追溯勾股定理的文化渊源

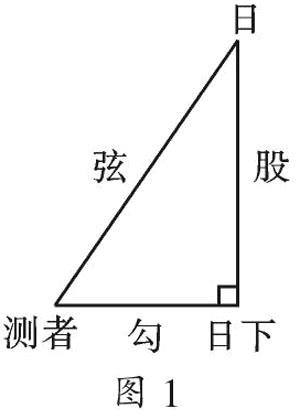
勾股定理从被发现至今已有5000多年的历史，5000多年来，世界上几个文明古国都相继发现和研究过这个定理.我国是最早了解勾股定理的国家之一，在4000多年前，我国人民就应用了这一定理.据我国一部古老的算书《周髀算经》记载，商高（约公元前1120年）答周公曰：“勾广三，股修四，径隅五”.这本书中同时还记载有另一位中国学者陈子（公元前7-前6世纪）与荣方在讨论测量问题时说的一段话：“若求邪（斜）至日者，以日下为勾，日高为股，勾股各自乘，并而开方除之，得邪至日.”如图1，即邪至日

这就是一般意义下的勾股定理.

2000多年前，古希腊的毕达哥拉斯（约公元前585年-公元前497年）在观察方形瓷砖密铺的地板面时，发现了勾股定理.因此，在国际上勾股定理又被称为毕达哥拉斯定理.

历史文献记载，商高知道特殊情况下的勾股定理比毕达哥拉斯学派至少要早五六个世纪，而陈子掌握普遍性的勾股定理的时间要比毕达哥拉斯早一二百年，无可争议，是我们的祖先最早发现勾股定理，我们为此而骄傲和自豪！

二、 体验勾股定理的发现过程

勾股定理是古人在测量土地、研究天文和制作工具的过程中，通过很多人的经验积累得到的.我们学习《勾股定理》时，也不妨体验一次勾股定理的发现过程，当一回小小数学家.

活动1：探究等腰直角三角形三边的关系.

问题：图2中正方形A、B、C的面积有何关系？你能归纳出正方形A、B、C所围成的等腰直角三角形三条边有什么特殊关系吗？

活动2：探究网格中直角三角形三边之间的关系.

问题1：在图3的方格纸中，每个小方格的面积均为1，三个正方形A、B、C的面积有何关系？

问题2：图3中正方形A、B、C所围成的直角三角形三条边之间有怎样的特殊关系？

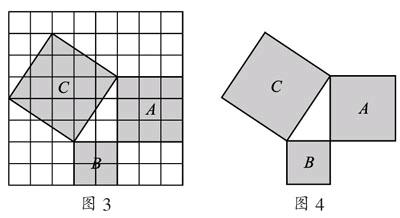
问题3：通过对等腰直角三角形及网格中的直角三角形三边关系的探究，你能对任意直角三角形三边关系提出一个合理的猜想吗？

问题4：如图4，直角三角形的两直角边长分别为a、b，斜边长为c，上面提出的猜想仍然成立吗？你有什么方法进行证明呢？

通过对特殊情形的观察与分析，进行合情推理，作出猜想，再对一般情形进行证明，得到所有直角三角形都具有这个性质，即如果直角三角形的两直角边长分别为a、b，斜边长为c，那么a2+b2=c2.

三、 感受勾股定理证明的魅力

勾股定理的证明方法层出不穷，至今已多达近四百种.由于《几何原本》的广泛流传，欧几里得的证明是勾股定理所有证明中最为著名的.

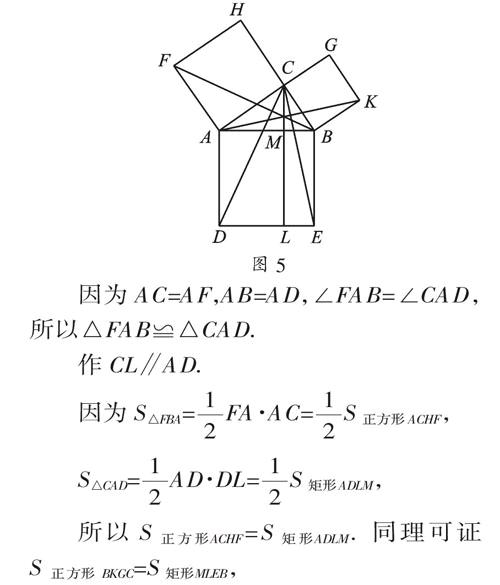
如图5所示，在直角三角形ABC各边上分别向外作正方形，连接CD、FB.

因为AC=AF，AB=AD，∠FAB=∠CAD，所以△FAB≌△CAD.

作CL∥AD.

所以S正方形ACHF=S矩形ADLM.同理可证S正方形BKGC=S矩形MLEB，

所以AB2=BC2+AC2，即a2+b2=c2.

为此，希腊人称之为“已婚妇女的定理”;法国人称之为“驴桥问题”;阿拉伯人称之为“新娘图”“新娘的坐椅”;在欧洲，又有人称之为“孔雀的尾巴”或“大风车”.

公元3世纪，我国古代数学家赵爽和刘徽分别对勾股定理作了证明.

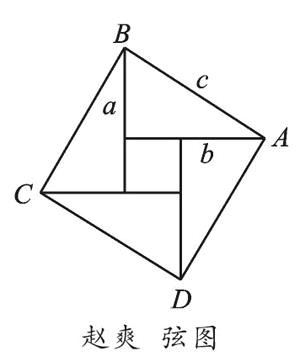
赵爽创制了“勾股圆方图”，又称“弦图”，以弦为边长得到正方形ABCD，把这个正方形分成四个全等的直角三角形和一个小正方形，每个直角三角形的面积为ab，中间的小正方形的面积为（a-b）2.于是便可得如下的式子：c2=（a-b）2+4×ab，化简得c2=a2+b2.他是世界上第一个用数形结合方法得到勾股定理的人.“赵爽弦图”是后世证明的先导，体现了图形割补的思想.

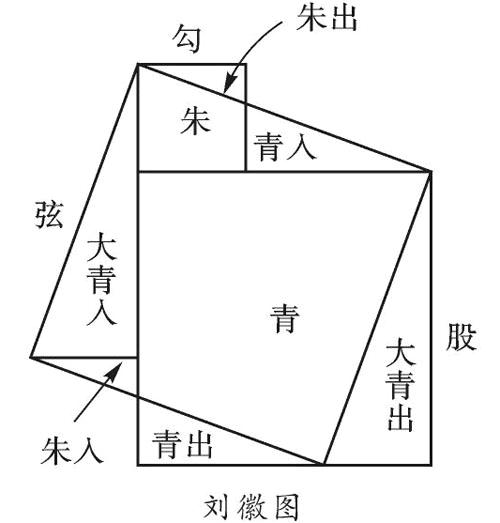
刘徽用了“青朱出入图”进行证明，他把勾股为边的正方形上的某些区域剪下来（出），移到以弦为边的正方形的空白区域内（入），结果刚好填满，勾股定理的证明便清晰地呈现.整个证明单靠移动几块图形而得出，也被称为“无字证明”.

我国古代数学家证明勾股定理是多么巧妙，多么简捷，融几何知识与代数知识于一体，体现了数与形的完美结合，真可谓独具匠心.

（作者单位：江苏省常州市兰陵中学）