常利率下分红稀疏风险模型的期望折现罚金函数

赵金娥, 李 明, 何树红

(1.红河学院 数学学院 云南 蒙自 661199； 2.云南大学 数学与统计学院 云南 昆明 650091)



常利率下分红稀疏风险模型的期望折现罚金函数

赵金娥1, 李 明1, 何树红2

(1.红河学院 数学学院 云南 蒙自 661199； 2.云南大学 数学与统计学院 云南 昆明 650091)

考虑到保险公司的投资收益及分红策略,建立常利率和常数红利边界策略下的稀疏风险模型,其中保费收入不再是时间的线性函数,而是一个复合Poisson过程,且索赔次数是保单到达数的稀疏过程.利用全期望公式及盈余过程的强马氏性,得到了期望折现罚金函数、破产时的Laplace变换、破产时赤字的期望折现以及破产概率满足的积分微分方程,并借助合流超几何函数给出指数保费和指数索赔下破产概率的具体表达式.

红利； 常利率； 期望折现罚金函数； 破产概率； 合流超几何函数

0 引言

风险理论主要研究和处理保险实务中的随机风险模型,并从定量角度分析保险公司经营的安全性,是当前精算界和数学学科研究的热门课题.传统的风险理论主要集中在对破产概率的研究,并且在大多数情况下只能得到破产概率的近似表达式或上界估计[1-3].1998年Gerber等[4]将破产时刻、破产前瞬时盈余和破产时赤字这三个破产理论中最为关注的精算指标融入到一个函数中,提出了期望折现罚金函数,这一重要函数的提出为研究破产理论带来极大便利,也在很大程度上推动了风险理论的发展,并出现了大量的研究成果[5-7].近年来随着人们对投资理财认知程度的提高以及保险业竞争的日益激烈,保险公司为了吸引更多的客户,推出了分红保险,这使得分红与破产问题成为当前保险管理及保险精算中备受关注的问题,而关于红利边界策略下经典风险模型的研究已较为透彻.自文献[8]首次提出常数红利边界策略下保费收入为复合Poisson过程风险模型以来,该模型已引起学者们的极大关注.考虑到保险实务中保单到达和索赔发生的相依性,文献[9]对文献[8]进行推广,研究了索赔次数是保单到达数的p-稀疏过程且保费随机收取风险模型的期望折现罚金函数和最优红利策略.

由于在保险公司的实际运营中,保险公司会将大部分的保费收入用于投资,并且投资所得占当前保险公司总收入的绝大部分,因此市场利率对保险公司的盈余将产生重要影响.作者在文献[9]的基础上考虑投资收益,建立常利率和常数红利边界策略下保费收入为复合Poisson过程,而索赔计数过程为保单到达过程的p-稀疏过程的风险模型.首先得到了模型的期望折现罚金函数满足的积分微分方程,然后通过期望折现罚金函数得到了破产时的Laplace变换、破产时赤字的期望折现以及破产概率满足的积分微分方程,最后在保费额与索赔额均服从指数分布的情形下借助合流超几何函数得到了破产概率的具体表达式,所得结果推广了文献[7]及文献[9]的相关结论.

1 模型介绍

定义1 设(Ω,F,P)是一完备概率空间,文中所涉及到的随机变量均定义在该空间上,则对t≥0,常利率下保险公司在t时刻的盈余过程为

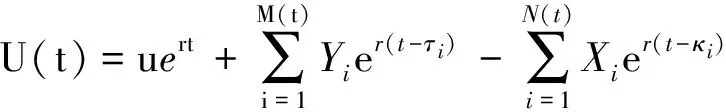
其中,r,u为非负常数,r表示常利率,u=U(0)是保险公司的初始资本；M(t)为至时刻t为止收到的保单数;Yi表示对第i份保单收取的保险费;τi为第i份保单到达的时刻；N(t)为至时刻t为止发生的索赔次数;Xi表示第i次的索赔额;κi为第i次索赔发生的时刻.

对上述模型作如下假设：

(1) 计数过程{M(t),t≥0}是强度为λ>0的Poisson过程,而{N(t),t≥0}是{M(t),t≥0}的p-稀疏过程；

(3) {M(t),t≥0},{Xi,i≥1}和{Yi,i≥1}相互独立.

给定红利界限b(u≤b),若保险公司的盈余超过红利界限b,超出部分全部用来分红,若盈余在红利界限以下便不发放红利.于是在该红利边界策略下保险公司的盈余过程{Ub(t),t≥0}可表示为

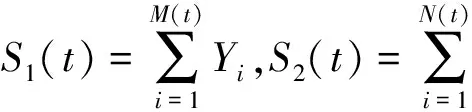
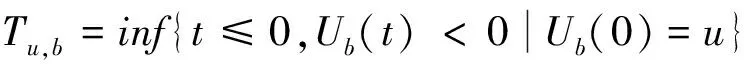
(1)

为破产时的期望折现罚金函数,也叫Gerber-Shiu函数.

显然,当ω(x,y)=y时,(1)式即为破产时赤字的期望折现

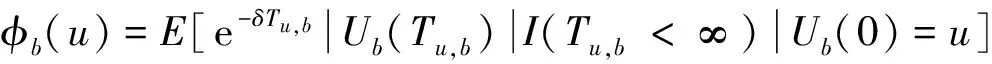
当ω(x,y)=1时,(1)式为破产时的Laplace变换,用φb(u)表示,即

当ω(x,y)=1且δ=0时,(1)式为破产概率

2 期望折现罚金函数

定理1 当0≤u≤b时,期望折现罚金函数mb(u)满足如下积分微分方程：

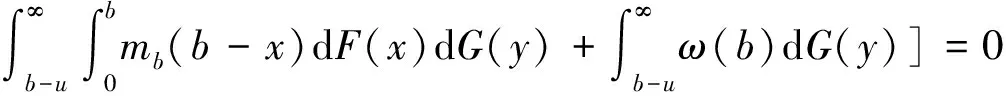
(2)

注1 当r=0时,(2)式即为文献[9]中的(3.6)式；当r=0且b→∞时,(2)式即为文献[7]中的(2.1)式.

证明 在无穷小的时间区间(0,Δt]上,利用盈余过程的强马氏性及全期望公式,有

mb(u)=E[mb(Ub(Δt))]=[1-λΔt+ο(Δt)]e-δΔtE[mb(uerΔt)]+

[(λΔt+ο(Δt))(1-p)]e-δΔtE[mb(uerΔt+Y)]+

[(λΔt+ο(Δt))p]e-δΔtE[mb(uerΔt+Y-X)]+ο(Δt).

(3)

由于

(4)

(5)

将(4)式和(5)式代入(3)式,有

两边同时除以Δt,并令Δt→0,有

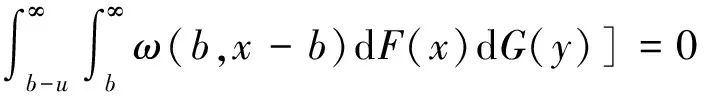
由此可得(2)式.

当u>b时,保险公司把超过b的那部分盈余全部进行分红,此时mb(u)=mb(b).

定理2 当0≤u≤b时,赤字的期望折现函数φb(u)满足如下积分微分方程：

(6)

当u>b时,φb(u)=φb(b).

注2 当r=0时,(6)式即为文献[9]中的(3.8)式.

证明 在(2)式中令ω(x,y)=y,即得结论.

定理3 当0≤u≤b时,破产时的Laplace变换满足如下积分微分方程：

(7)

当u>b时,φb(u)=φb(b).

注3 当r=0时,(7)式即为文献[9]中的(4.1)式.

证明 略.

定理4 当0≤u≤b时,破产概率ψb(u)满足如下积分微分方程：

(8)

当u>b时,ψb(u)=ψb(b).

证明 略.

3 破产概率的具体表达式

一般情形下很难给出以上积分微分方程的精确解,但在索赔额与保费额均服从指数分布时可得到破产概率的精确表达式.

设F(x)=1-e-αx(x>0),G(y)=1-e-βy(y>0),则(8)式为

(9)

(9)式两边对u求导,有

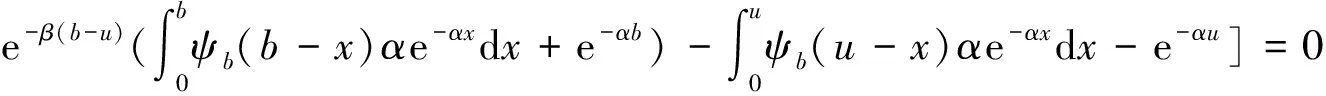
(10)

(10)式两边再对u求导,有

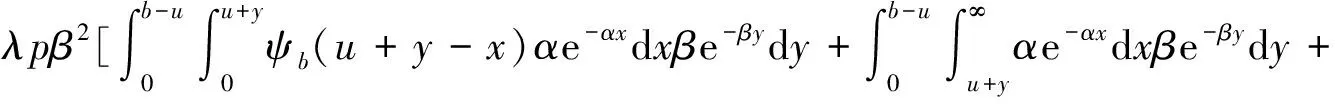
(11)

由(9)～(11)式,有

(12)

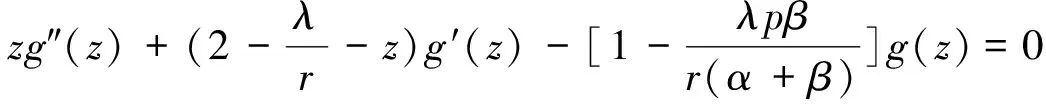
解之得

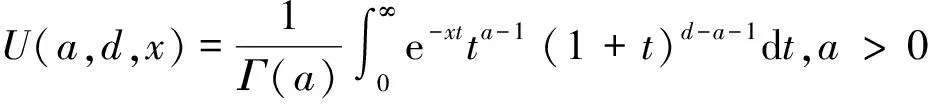
分别是第一类和第二类合流超几何函数.所以

A1h1(u)+A2h2(u),

所以

ψb(u)=A0+A1H1(u)+A2H2(u),

这里

又由文献[10]有ψb(0)=1及ψb(+∞)=0,故A0=1,且

1+A1H1(+∞)+A2H2(+∞)=0.

(13)

在(9)式中令u=b,有

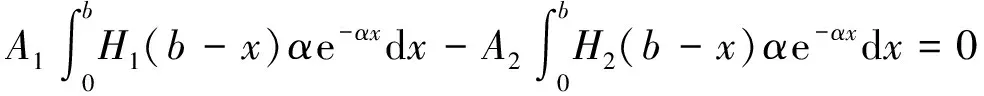
(14)

联立(13)和(14)式,解得

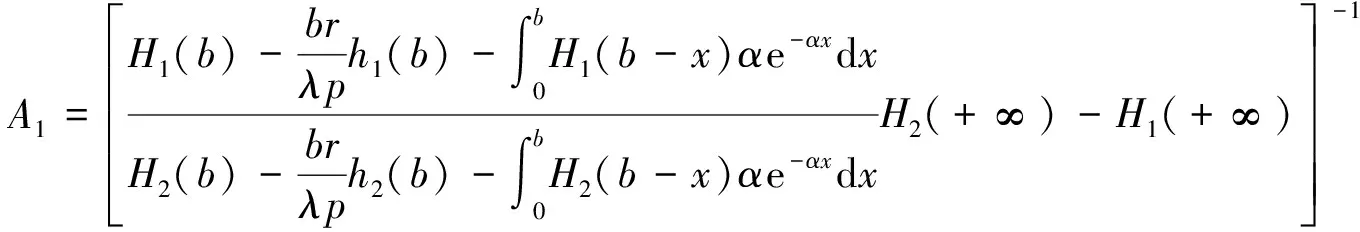
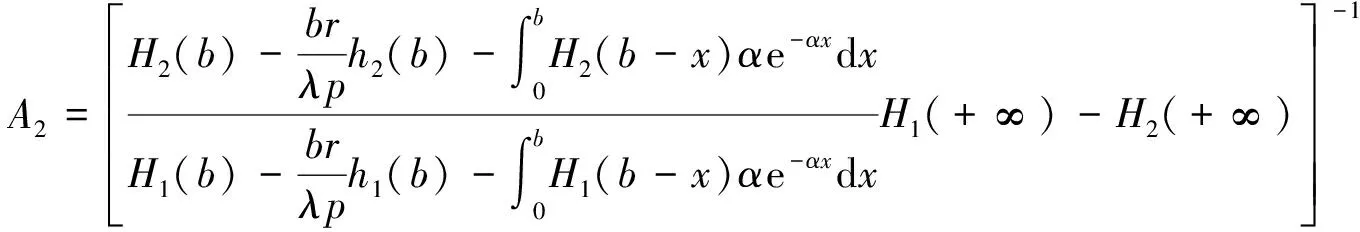
[1] 杨洋,林金官,高庆武.时间相依更新风险模型中无限时绝对破产概率的渐近性[J].中国科学:数学,2013,43(2):173-184.

[2] 刘超,王永茂,颜玲,等.带干扰的多险种二项风险模型的破产概率[J].郑州大学学报:理学版,2012,44(1):46-49.

[3]AvramF,PistoriusM.OnmatrixexponentialapproximationsofruinprobabilitiesfortheclassicandBrownianperturbedCramér-Lundbergprocesses[J].Insurance:MathematicsandEconomics, 2014,59(11):57-64.

[4]GerberHU,ShiuESW.Onthetimevalueofruin[J].NorthAmericanActuarialJournal, 1998,2(1):48-78.

[5]LiShuanming,LuYi.Ontheexpecteddiscountedpenaltyfunctionfortwoclassesofriskprocesses[J].Insurance:MathematicsandEconomics, 2005,36(2):179-193.

[6] 戴洪帅，唐沧新.随机投资收益风险过程的一个标注[J].河南科技大学学报:自然科学版,2014,35(1):101-104.

[7]PanJie,WangGuojing.Expecteddiscountedpenaltyfunctionforathinningriskmodel[J].ChineseJournalofAppliedProbabilityandStatistics, 2009,25(5):544-552.

[8]XiangMingyin,WeiJiaqin.Optimaldividendstrategyundertheriskmodelwithstochasticpremium[J].ChineseJournalofAppliedProbabilityandStatistics, 2011,27(1):39-46.

[9] 赵金娥,李明,何树红.一类稀疏风险模型的Gerber-Shiu函数和最优红利策略[J].应用概率统计,2014,30(4):439-448.

[10]方世祖,罗建华.双复合Poisson风险模型[J].纯粹数学与应用数学,2006,22(2):271-278.

(责任编辑：孔 薇)

The Expected Discounted Penalty Function for a Thinning Risk Model with Constant Interest and Dividends

ZHAO Jin-e1, LI Ming1, HE Shu-hong2

(1.CollegeofMathematics,HongheUniversity,Mengzi661199,China;2.CollegeofMathematicsandStatistics,YunnanUniversity,Kunming650091,China)

Considering the insurance company’s investment income and dividend strategy, a thinning risk model was established. In contrast with the classical risk model where the premium process was a linear function of time, the aggregate premium process was a compound Poisson process and the claim number process was a thinning process of the premium arriving number process. Moreover, there were a constant interest and a constant dividend barrier strategy in this model. By taking full advantage of the total expectation formula and the strong Markov property of the surplus process, the integro-differential equations for the expectation discounted penalty function, the Laplace transform of the time of ruin, the discounted expectation of the deficit at ruin and the ruin probability were derived. Meanwhile, the explicit expression for the ruin probability was given in terms of the confluent hypergeometric functions when the individual stochastic premium amount and claim amount were exponentially distributed.

dividend; constant interest; expected discounted penalty function; ruin probability; confluent hypergeometric function

2015-05-30

国家自然科学基金资助项目,编号11301160;云南省科技厅自然科学研究基金资助项目,编号2013FZ116;云南省教育厅科研基金资助项目,编号2013C014；红河学院科研基金资助项目，编号XJ15SX06.

赵金娥(1978-),女,云南大理人,讲师,硕士,主要从事保险风险理论研究,E-mail:zhaojine0829@163.com;通讯作者：李明(1983-),男,湖南长沙人,讲师,硕士,主要从事偏微分方程数值解研究,E-mail:mathlm@126.com.

赵金娥,李明,何树红.常利率下分红稀疏风险模型的期望折现罚金函数[J].郑州大学学报：理学版，2015,47(3)：37-42.

O211.67

A

1671-6841(2015)03-0037-06

10.3969/j.issn.1671-6841.2015.03.007