关于解一类奇异非线性方程组的牛顿法的收敛性
2015-12-27杨家岭曹德欣
杨家岭, 曹德欣
(中国矿业大学 理学院 江苏 徐州 221116)
关于解一类奇异非线性方程组的牛顿法的收敛性
杨家岭, 曹德欣
(中国矿业大学 理学院 江苏 徐州 221116)
对一类奇异非线性方程组,运用Moore-Penrose广义逆建立牛顿迭代法,分析了其局部收敛性、半局部收敛性以及收敛半径的估计,数值例子也表明了算法的有效性.
奇异非线性方程组; 牛顿法; Moore-Penrose逆; 半局部收敛
0 引言
许多应用数学和工程问题都可归结为对非线性方程组的求解[1-3], 其中也存在着大量的奇异非线性方程组, 并且引起了人们的广泛关注[4-7].作者考虑如下形式的奇异非线性方程组的求解问题:
F(x)=0,
(1)
这里F:D⊂Rn→Rm,F(x)=(f1(x),f2(x),…,fm(x))T,x=(x1,x2,…,xn)T,n≤m.
牛顿迭代格式
xk+1=xk-DF(xk)-1F(xk),k=0,1,…
(2)
及其变形是求解非线性方程组最有效的方法. 关于牛顿法的收敛性有两个最为重要的结果: 一是著名的Kantorovich定理[8], 其半局部收敛性定理及证明方法对迭代法的研究产生了深远的影响;二是Smale点估计理论[9], 该定理给出了仅依赖于算子在初始点的信息来逼近零点的判断依据. 关于牛顿法收敛半径的估计还可以参见文献[10-11].
对于方程组(1)而言,F的Frechet导算子DF(xk)不一定可逆, 尤其是当n xk+1=xk-DF(xk)†F(xk),k=0,1,… (3) 格式(3)的不动点x*是方程组F(x)=0的最小二乘解, 但若DF(x*)是满秩, 则x*是方程组F(x)=0的解. 对于n≥m情况下的奇异问题,文献[4-7]已经进行了详细的论述, 特别是文献[7]对F在初始点x0∈D处的Jacobian矩阵J(x0)为行满秩的条件下研究了(3)式的收敛性. 那么, 对于n≤m情况下的奇异问题, 在J(x0)对应为列满秩的条件下是否有相关的结论呢?在研究方法上与文献[7]又有何异同?由于列满秩的J(x0)与行满秩的J(x0)所对应的Moore-Penrose逆矩阵的性质有很大差异, 所以要想得到相关的结果就必须在方法上另找出路. 作者将重新定义Lipschitz条件, 在DF(x*),DF(x0)为列满秩,DF(x)DF(x*)†及DF(x)DF(x0)†满足新定义的Lipschitz条件下, 求解奇异非线性方程组(1)的牛顿迭代格式(3)的收敛判据, 并得出了(3)式的局部收敛性、半局部收敛性和收敛半径的估计. 设A∈Rm×n, 则A†称为A的Moore-Penrose逆, 若下列4个等式成立: AA†A=A,A†AA†=A†, (AA†)T=AA†, (A†A)T=A†A. 令kerA和ImA表示A的核与象,∏E表示Rn在子空间E⊂Rn上的正交投影,E⊥表示E在Rn上的正交补空间. 则有 A†A=∏(ker A)⊥,AA†=∏Im A. (4) 当A为列满秩时,有 A†A=IRn, (5) 更多关于Moore-Penrose逆的结果可参见文献[12]. 定义1 设常数L>0, 实数r>0,x*∈Rn且DF(x*)为列满秩,则称DF(x)DF(x*)†在B(x*,r)中满足关于L的中心Lipschitz条件, 若 ‖(DF(x)-DF(x*))DF(x*)†‖≤L‖x-x*‖, ∀x∈B(x*,r). (6) 证明 由(6)式可以得到 ‖(DF(x)-DF(x*))DF(x*)†‖≤L‖x-x*‖<1, 由Banach引理得到IRm-(DF(x*)-DF(x))DF(x*)†可逆, 注意到 IRm-DF(x*)DF(x*)†=∏(Im DF(x*))⊥, 所以 IRm-(DF(x*)-DF(x))DF(x*)†=∏(Im DF(x*))⊥+DF(x)DF(x*)†. 因此∏(Im DF(x*))⊥+DF(x)DF(x*)†可逆,根据(5)式, DF(x*)†DF(x*)=IRn, 及 DF(x)=(∏(Im DF(x*))⊥+DF(x)DF(x*)†)DF(x*), 又因为DF(x*)为列满秩, 从而对任意一点x∈B(x*,r),DF(x)为列满秩. 引理2[12]设A∈Rm×n,rank(A+E)=rank(A)且‖A†‖2‖E‖2<1,则 (7) ‖DF(x′)-DF(x″)‖<ε, (8) 当然对∀x∈B(x*,δ),也有 ‖DF(x)-DF(x*)‖<ε. rank(DF(x))=rank(DF(x*)). rank(A+E(x))=rank(A), 并且有 (9) 所以根据引理2可得 (10) 现任取x0∈B(x*,r), 假设由格式(3)产生的点xk∈B(x*,r), 并且根据DF(xk)†DF(xk)=IRn及Banach空间微分中值定理, 不等式(10)及DF(x)在B(x*,r)中的一致连续性可以得到 ‖xk+1-x*‖=‖xk-x*-DF(xk)†F(xk)‖= ‖xk-x*-DF(xk)†F(xk)+DF(xk)†F(x*)‖= ‖xk-x*-DF(xk)†(F(xk)-F(x*))‖= ‖DF(xk)†DF(xk)(xk-x*)-DF(xk)†(F(xk)-F(x*))‖≤ ‖DF(xk)†‖‖DF(xk)(xk-x*)-(F(xk)-F(x*))‖≤ ‖(DF(x′)†-DF(x″)†)F(x″)‖≤α‖x′-x″‖,α<1, (11) (12) ε0‖DF(x)†‖+α≤ε0N+α∶=M<1. (13) ‖DF(x′)-DF(x″)‖<ε0. (14) (i) 对所有k=0,1,…, 下列两式成立: (15) (16) (i)的证明. 由定理2的假设知, 当k=0时, 结论成立; 设j=1,…,k-1时结论成立, 即有 (17) 由(17)得 由格式(3)得 xk+1-xk=-DF(xk)†F(xk)=xk-xk-1-DF(xk)†F(xk)+DF(xk-1)†F(xk-1). 由于DF(xk-1)†DF(xk-1) =IRn, 故 xk+1-xk=DF(xk-1)†DF(xk-1)(xk-xk-1)-DF(xk)†F(xk)+DF(xk-1)†F(xk-1)= -DF(xk-1)†(F(xk)-F(xk-1)-DF(xk-1)(xk-xk-1))+(DF(xk-1)†-DF(xk)†)F(xk). 所以 ‖xk+1-xk‖≤‖-DF(xk-1)†(F(xk)-F(xk-1)-DF(xk-1)(xk-xk-1))‖+ ‖(DF(xk-1)†-DF(xk)†)F(xk)‖≤ ‖(DF(xk-1)†-DF(xk)†)F(xk)‖. 由(16), (14)和(11)得 ‖xk+1-xk‖≤‖DF(xk-1)†‖ε0+α‖xk-xk-1‖. 再由(13)和(17)式得到 (18) 这样就根据数学归纳法证明了(15)式,从而证明了(i)的结论. (ii)的证明.当m≥n时, 由(15)式可得 ‖xm+1-xn‖≤‖xm+1-xm‖+‖xm-xm-1‖+…+‖xn+1-xn‖< (19) 因为DF(x∞)†为列满秩, 从而F(x∞)=0. (iii)的证明. 由(19)式得 (20) 定理2证毕. 下面给出一个相关的数值例子: (21) 方程F(x)=0的精确解是x*=(1,1,0)T, 相应的Jacobian矩阵是 且J(x*)为列满秩矩阵. 数值试验结果参见表1和表2. 表1 以x0=(0.3,0.4,0.25)T为初值的数值结果Tab.1 The numerical results with initial value of x0=(0.3,0.4,0.25)T 表2 以x0=(1.4,1.5,-0.2)T为初值的数值结果Tab.2 The numerical results with initial value of x0=(1.4,1.5,-0.2)T 从表1可以看出实验数值稳定并逐渐趋向于方程组的解,并且从表2可知,如果初值选取恰当数值,收敛速度也较快. 另外, 从定理1和定理2的证明中可以看到, 若再有DF(x)关于某一常数满足Lipschitz条件, (11)式的条件再稍加强一些, 则可以得到格式(3)的更高阶的收敛性. [1] 贺婷婷,马飞遥.两个非线性偏微分方程强解的持续性质[J].郑州大学学报:理学版,2015,47(1):14-23. [3] Dedieu J P.Estimations for the separation number of a polynomial system[J].J Symbolic Comput,1997,24(6):683-693. [4] Decker D W,Keller H B, Kelley C T.Convergence rates for Newton’s method at singular points[J].SIAM J Numer Anal,1983,20(2):296-314. [5] Griewank A.On solving nonlinear equations with simple singularities or nearly singular solutions[J].Siam Rev,1985,27(4):537-563. [6] Allgower E L,Böhmer K.Resolving singular nonlinear equations[J].Rocky Mount J Math,1988,18(2):225-268. [7] 吴国桢,王金华.关于奇异非线性方程组的Newton法的收敛性[J].浙江大学学报:理学版,2008,35(1):27-31. [8] Kantorovich L V,Akilov G P.Functional Analysis[M].Oxford: Pergamon Press,1982:536-544. [9] Smale S.Newton’s method estimates from data at one point[M]//Ewing R E,Gross K I,Martin C F.The Merging of Disciplines: New Directions in Pure, Applied and Computational Mathematics. New York: Springer,1986:185-196. [10]Traub J F,Wózniakowski H.Convergence and complexity of Newton iteration for operator equations[J].J Assoc Comput Math,1979,26(2):250-258. [11]王兴华.Newton 方法的收敛性[J].科学通报: 数理化专辑,1980,25(1):36-37. [12]Wang Guorong,Wei Yimin,Qiao Sanzheng.Generalized Inverses: Theory and Computations[M].Beijing: Science Press,2004:5-7. (责任编辑:孔 薇) Convergence Property of Newton’s Method for Solving a Class of Singular Nonlinear Equations YANG Jia-ling, CAO De-xin (CollegeofSciences,ChinaUniversityofMiningandTechnology,Xuzhou221116,China) Moore-Penrose inverse was used to construct Newton’s method for solving a class of singular nonlinear equations. The local and semilocal convergence were established, and the radius of convergence ball was also obtained. The validity of the algorithm was indicated by a numerical example. singular nonlinear equations; Newton’s method; Moore-Penrose inverse; semilocal convergence 2015-06-25 国家自然科学基金资助项目,编号70901073;中央高校基本科研业务费专项资金资助项目,编号JGK101676. 杨家岭(1988-),男,安徽六安人,硕士研究生,主要从事方程数值解及数值优化研究,E-mail: aa603781849@163.com;通讯作者:曹德欣(1962-),男,河北石家庄人,教授,博士生导师,主要从事方程数值解、数值优化、区间算法及智能算法研究. 杨家岭,曹德欣.关于解一类奇异非线性方程组的牛顿法的收敛性[J].郑州大学学报:理学版,2015,47(3):1-6. O241 A 1671-6841(2015)03-0001-06 10.3969/j.issn.1671-6841.2015.03.0011 预备知识




2 牛顿法的局部收敛性









3 牛顿法的半局部收敛性












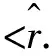

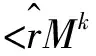




4 数值例子




