梯形区域下执行器增益偏差容忍区间的分析

于　洁，王福忠，姚　波，王维宏

(1.沈阳师范大学 数学与系统科学学院，辽宁 沈阳 110034；

2.沈阳工程学院 a.基础教学部; b.教务处，辽宁 沈阳 110136)



梯形区域下执行器增益偏差容忍区间的分析

于洁1，王福忠2a，姚波1，王维宏2b

(1.沈阳师范大学 数学与系统科学学院，辽宁 沈阳 110034；

2.沈阳工程学院 a.基础教学部; b.教务处，辽宁 沈阳 110136)

摘要：针对执行器故障，建立执行器某一条通道的增益偏差模型，在梯形区域极点配置下，利用LMI给出了各个通道的增益偏差容忍区间的算法，并计算得到执行器各个通道的增益偏差容忍区间。通过计算结果的对比，了解了各个通道对闭环系统的影响程度，判断了是否该加强某一通道的硬件个数，为梯形区域极点配置中是否增减执行器通道硬件提供了理论依据，并通过仿真示例说明了该方法的正确性和有效性。

关键词：容忍区间；梯形区域极点配置；执行器通道；冗余度

冯诺伊曼在1962年提出了容错的基本思想。近几年里，容错控制在很多领域都有所应用[1-2]。文献[1]主要研究的是容错飞行控制系统中控制器的设计。文献[2]研究的是车辆悬架系统除执行器故障自适应PID滑模的容错控制方法。被动容错控制又称可靠控制，近几年来，有许多学者取得了很多成就[3-8]。文献[3-5]主要研究的是离散系统的可靠控制问题。文献[6-8]主要研究的是线性系统的可靠控制问题。在线性系统中，可靠极点配置是控制器设计的重要手段，有很多的学者给出了将极点配置在不同区域的配置方法[9-15]。文献[9]研究的是具有区域极点约束的可靠控制器设计。文献[10-12]主要是针对圆盘内可靠控制器的设计。文献[13]给出了在部分扇形区域内可靠控制器的设计。文献[14]是在文献[9]和文献[13]的基础上，给出了在梯形区域内可靠控制器的设计。但是，如果控制器可靠了，又会增加系统的保守性，也会增加消耗，那么硬件冗余的设计就很有必要了。在这一方面也有学者做过研究，文献[15]主要研究的是一类线性系统，在圆盘区域极点配置的条件下，当执行器出现故障时，提出了容忍区间的概念及其算法。

在这些研究结果的基础之上，提出了在梯形区域极点配置下容忍区间的概念，并在线性系统的条件下给出了执行器第i条通道增益值容忍区间的算法。

1线性系统问题描述

考虑具有如下形式的线性系统：

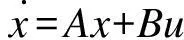
(1)

(1)式中，x∈Rn是系统的状态向量，u∈Rm是执行器的信号向量，A和B是适维常值矩阵，且有

u=Kx

(2)

引理 1[9]：对于线性系统(1),使得系统矩阵A的所有特征值均配置在由h1、h2组成的垂直条形区域内的充分必要条件是：存在正定对称的矩阵X，使得(3)式成立。

(3)

引理 2[9]：对于线性系统(1),使得系统矩阵A的所有特征值均配置在以θ为夹角的广义扇形区域内的充分必要条件是：存在正定对称的矩阵X，使得(4)式成立。

(4)

引理 3[14]：对于线性系统(1)，存在增益矩阵K，使得系统的极点配置到D(h1,h2)、Dθ的共同区域内的充分必要条件是：存在正定对称矩阵X和矩阵P，使得式(5)、(6)同时成立。其中，B1=AX+BP。

(5)

(6)

当系统的执行器有故障时，原系统可以表述为如下形式：

(7)

考虑执行器通道的增益偏差模型，假设系统第i条通道出现了故障，则：

uf=Miu

(8)

其中，Mi和fi分别为

引入如下符号，以便表达：

1)eig(A)表示对矩阵A求特征值；

2) λij表示执行器第i条通道出现故障时系统统的第j个特征值；

3)Re[λ]表示λ的实部值；

4)Im[λ]表示λ的虚部值；

5)Max(a,b)表示取a,b中的最大值；

6)Min(a,b)表示取a,b中的最小值。

(9)

根据定义可以知道，如果容忍区间越大，那么该条通道的故障增益值被容许的波动范围就越大；如果硬件冗余度越小，那么该条通道的故障对系统的可靠性影响就越小。反之，如果容忍区间越小，那么该通道的故障增益值可以波动的范围就小了，当然可靠性就重要了，该信号通道需要的硬件冗余度就大了。

2容忍区间分析

定理对于上述闭环系统(9)，下列优化问题有解，其中目标函数为

(10)

约束条件为

(11)

(12)

(13)

h1≤xij≤h2

(14)

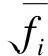
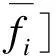
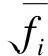
证毕。

3仿真示例

参考一个CH-47双旋翼直升飞机的线性模型：

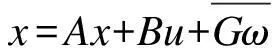
其中，y1为垂直速度(节/h)，y2为倾斜角度(弧度)。

控制输入：u1为集流螺旋桨推力，u2为差动集流螺旋桨推力[16]。

规定故障值波动的范围如下：

0.1≤f1,f2≤1.5

经过计算该系统的矩阵A的极点为

v1=-2.227 9，v2=0.065 2，

v3=0.491 3+0.415 1i，v4=0.491 3-0.415 1i。

显然系统是存在右侧极点的，可以得知原系统并不稳定。

计算机仿真结果如下：

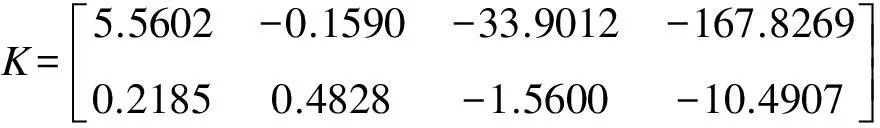
可将此不稳定系统的极点配置到D(h1,h2)、Dθ的梯形区域内，如图1所示。图2和图3分别是闭环系统(9)执行器第一条通道和第二条通道故障增益波动引起的系统的极点分布图。从图中可以看出，当存在故障增益波动时，闭环系统(9)的极点一部分在梯形区域内，一部分在梯形区域外，明确了当故障增益波动时极点仍在梯形区域内的增益波动范围，即执行器通道故障增益波动的容忍区间。

要想得到梯形区域极点配置下的故障增益容忍区间，需要满足两个条件：一个是闭环系统极点的实部在执行器增益波动时可以保持在指定的变化范围内；另一个是闭环系统极点的虚部与实部的比值在执行器增益波动时可以保持在指定的变化范围内。两条同时满足时，就是执行器第i条通道故障增益波动的容忍区间。

执行器第一条通道极点实部随故障增益波动变化曲线如图4所示。横向两条直线h1、h2表示xi、i=1,2,3,4的变化范围，纵向两条直线f1、f2表示执行器第一条通道故障增益值f1变化的范围，曲线x1，x2，x3，x4表示闭环系统的4个极点的实部值在执行器第一条通道故障参数f1变化时的变化情况。由此可知，使闭环系统的4个极点的实部均在由h1,h2,f1,f2四条直线围成的矩形内的故障增益变化的范围，就是满足定理的f1的变化范围，即[0.408 9，1.038 1]。

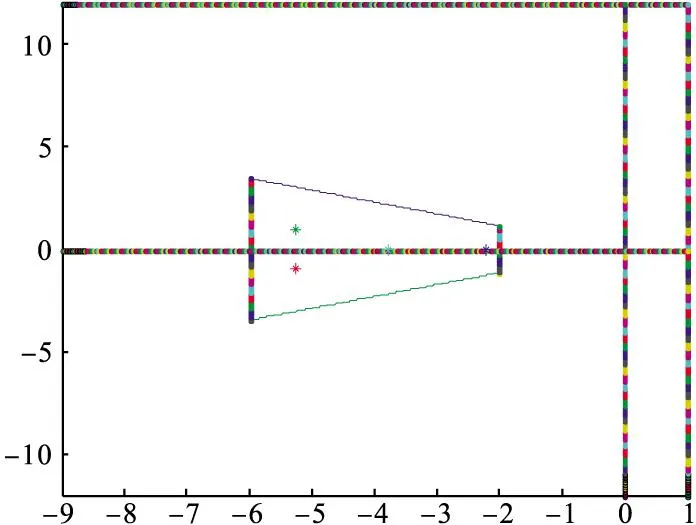
图1　定常闭环系统梯形区域极点分布

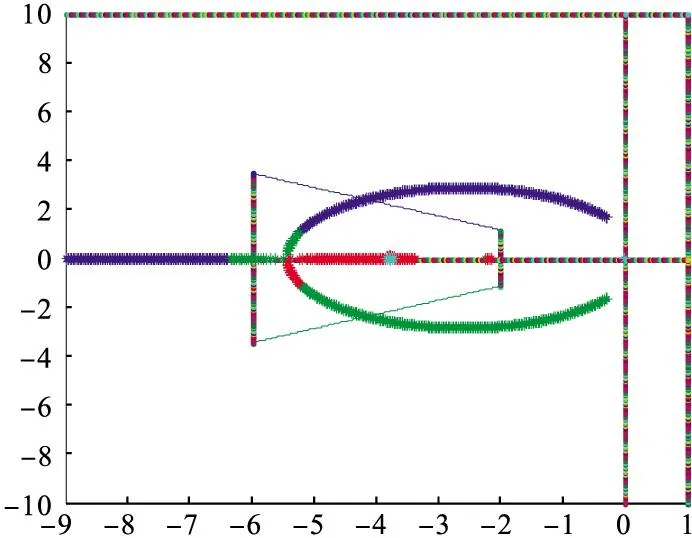
图2　闭环系统执行器第一条通道故障增益

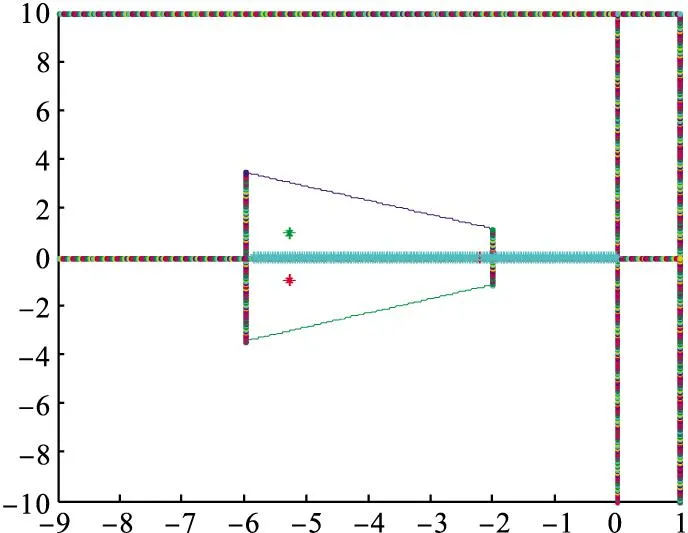
图3　闭环系统执行器第2条通道故障增益

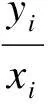
图4　执行器第一条通道极点实部随故障

图5　执行器第一条通道故障增益波动引起的

综上所述，执行器第一条通道故障增益波动容忍区间是[0.799 8，1.038 1]。

图6表示闭环系统的4个极点实部值随第二条通道故障参数f2变化时分别变化的情况，其原理与图4相同，满足条件的f2的范围是[0.582 1，1.500 0]。

图7表示闭环系统的4个极点虚部与实部比值随执行器第二条通道故障参数f2变化时的变化情况，其原理与图5相同，满足条件的f2的范围是[0.1，1.5]。

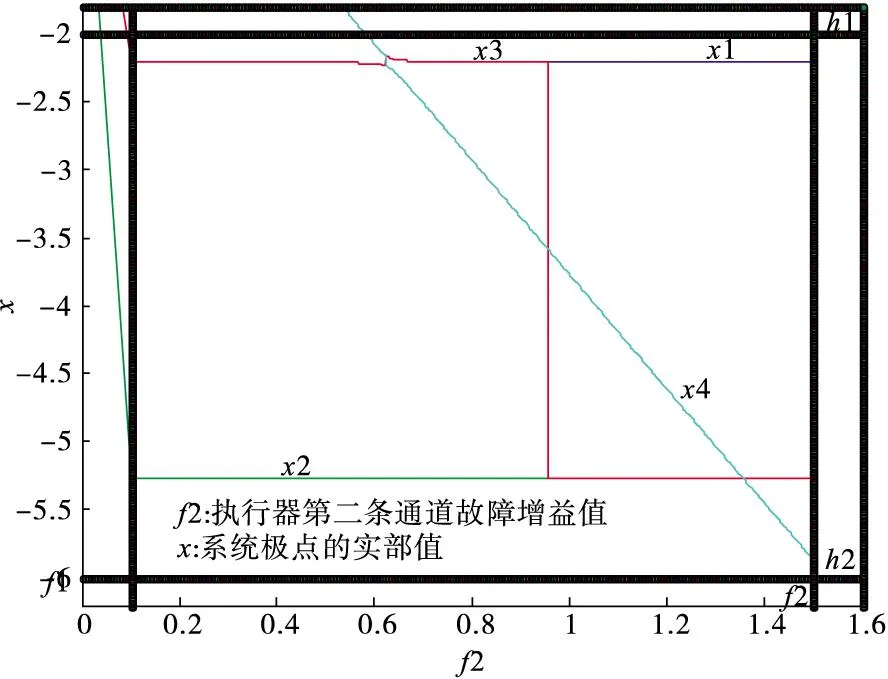
图6　执行器第二条通道极点实部随故障

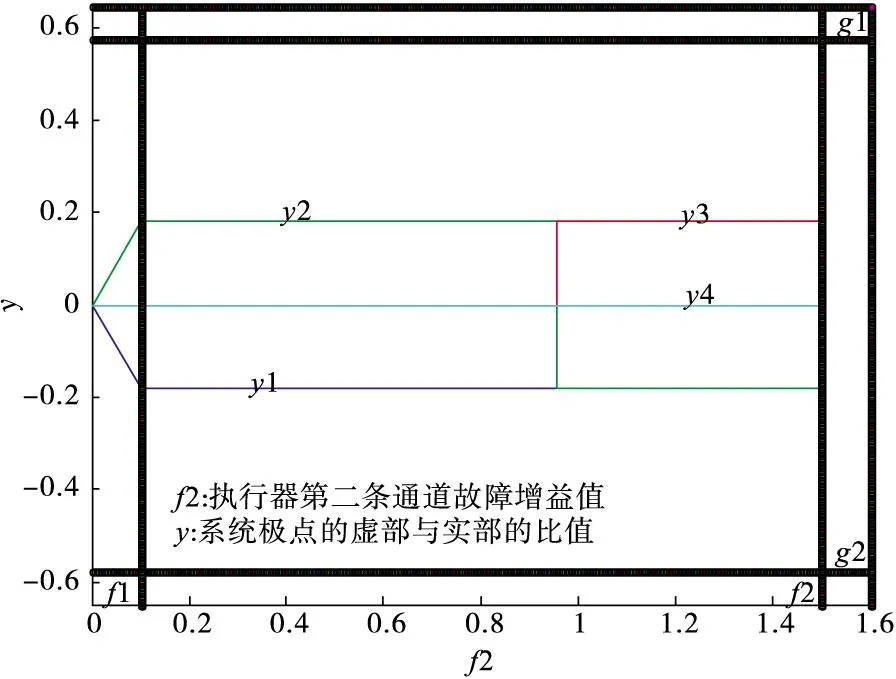
图7　执行器第二条通道故障增益波动引起的

由图6和图7分析可知，执行器第二条通道故障增益波动容忍区间是[0.582 1,1.500 0]。

综上所述，故障增益的波动对u1的影响较大，对u2的影响就比较小了。那么就可以根据以上数据分析的结果来加强执行器第一条通道的硬件个数，降低该信号通道故障对飞机稳定性造成的影响，从而提高飞机的可靠性，使CH-47能够稳定的飞行。

4结论

根据上述分析结果确定了在线性系统中，满足梯形区域极点配置下，执行器单一通道故障增益偏差容

忍区间的算法，验证了提出的定理能有效地算出每条通道的容忍区间，通过对具体实例的分析，可以有针对性地增加某一信号通道的执行器数量，既提高了该通道信号的准确传递，又避免了不必要的浪费，节省成本。

参考文献

[1]Xiang Yu,Jin Jiang.Hybrid Fault-Tolerant Flight Control System Design Against Partial Actuator Failures[J].IEEE Transactions On Control Systems Technology,2012,20(4):871-886.

[2]Morteza Moradi,Afef Fekih.Adaptive PID-Sliding-Mode Fault-Tolerant Control Approach for Vehicle Suspension Systems Subject to Actuator Faults[J].IEEE Transactions on Vehicular Technology,2014,63(3):1041-1054.

[3]Veillette R J,Medanic J V,Perking W R.Design of reliable control system[J].IEEE Transaction on Automatic Control,1992,37(3):290-304.

[4]Yang G H,Wang J L,Son Y C.Reliable controller design for linear systems with sensor with sensor failures.Proceeding of the 37th IEEE conference on decision and control[C].Tampa,Florida，1998b,2822-2827.

[5]Shaolong Shu,Feng Lin.Fault-Tolerant Control for Safety of Discrete-Event Systems[J].IEEE Transactions On Automatic Science And Engineering,2014,11(1):78-89.

[6]Yang G H,Wang J L,Son Y C.Reliable controller design for linear systems [J].Auto-matica,2001,37(3):717-725.

[7]王福忠，姚波，张嗣赢.线性系统区域稳定的可靠控制[J].控制理论与应用，2004,21(5):835-839.

[8]王福忠，姚波.线性系统可靠控制分析与设计[M].沈阳：辽宁科学技术出版社，2012.

[9]俞立.鲁棒控制—线性矩阵不等式方法[M].北京：清华大学出版社，2002.

[10]Furuta K Im S B.Pole Assignment in a Specified Disk[J].IEEE Transaction on Automatic Control,1987,32(5):423-427.

[11]姚波，张庆灵，王福忠.具有传感器故障的可靠圆盘极点配置[J].控制与决策，2004,19(3):346-348.

[12]孙欣，徐兆棣，姚波.考虑执行器故障圆盘极点可靠配置[J].计算技术与自动化，2005,24(4):35-37.

[13]姚波，王福忠.部分扇形区域极点配置的可靠控制[J].计算技术与自动化，2004,23(4):4-6,10.

[14]郭一珂，王福忠.考虑执行器故障梯形区域极点的可靠配置[J].计算技术与自动化，2012,31(1):15-20.

[15]王福忠，辛健.基于极点配置执行器增益偏差容忍区间的分析[J].控制工程，2012,19(5):740-742.

(责任编辑张凯校对佟金锴)

The Analysis of Actuator Gain Error Tolerate

Interval Based on Trapezoidal area

YU Jie1,WANG Fu-zhong2,YAO Bo1，WANG Wei-hong2

(1.College of Mathematics and System Science,Shenyang Normal University,Shenyang 110034;

2a.Department of Preparatory Course; 2b.Academic Affair Office,Shenyang Institute of

Engineering,Shenyang 110136,Liaoning Province)

Abstract：One channel gain bias model of actuator was established in this paper to deal with the actuator failures.The gain deviation tolerance interval algorithm of each channel was given,and the tolerance range of each channel was calculated with LMI under the trapezoidal regional pole assignment.By comparing the calculation results,the influence degree on each channel of the closed-loop system and whether increase the hardware number of one channel was known.This algorithm provides a theoretical foundation to increase or decrease the hardware number of actuator channel under the trapezoidal regional pole assignment and a simulation example shows its correctness and effectiveness.

Key words：tolerate interval;trapezoidal area pole placement;actuator channel;redundancy rate

通讯作者：王福忠(1963-)，男，辽宁沈阳人，教授，博士，硕士生导师，主要从事模糊控制、动态系统的鲁棒控制和容错控制方面的研究。

作者简介：于洁(1988-)，女，辽宁大连人，硕士研究生。

基金项目：辽宁省自然科学基金(201202200)；辽宁省教育厅高等学校科学研究项目(L2011236)

收稿日期：2015-03-06

中图分类号：TP13

文献标识码：A

文章编号：1673-1603(2015)02-0171-05

DOI：10.13888/j.cnki.jsie(ns).2015.02.018