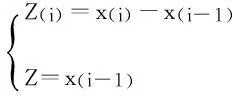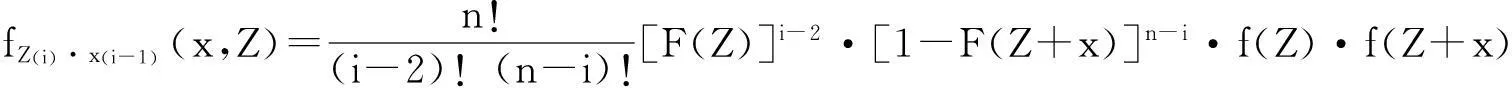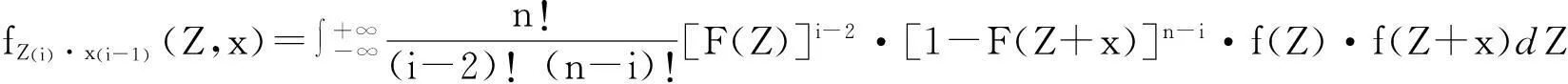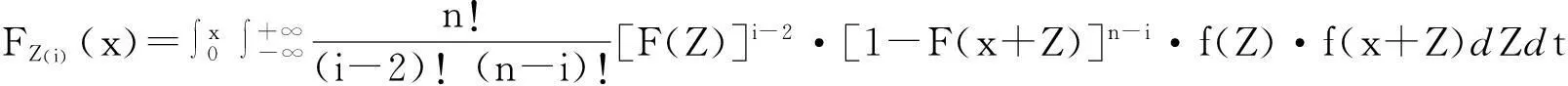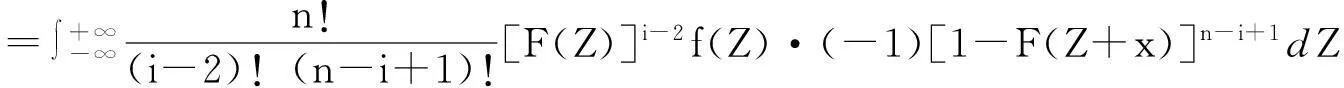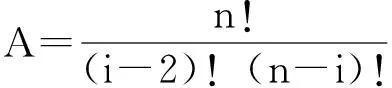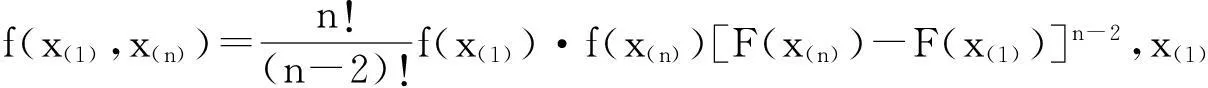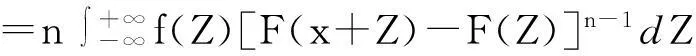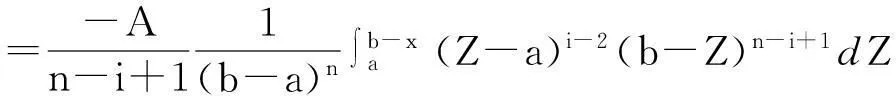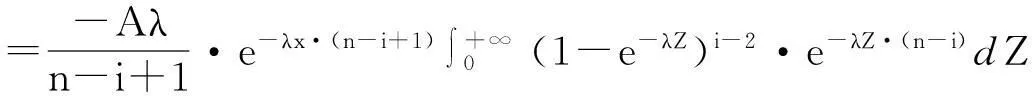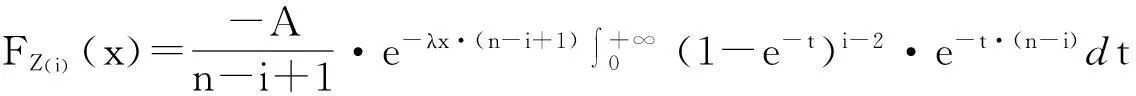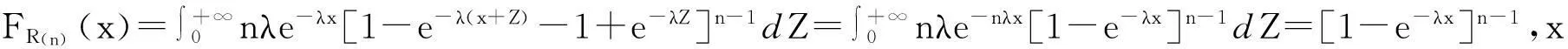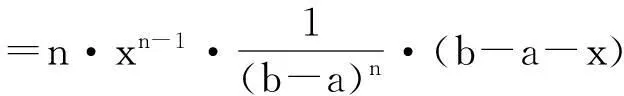差分与极差的分布函数
2015-12-26文小波
差分与极差的分布函数
文小波
(四川民族学院数学系,四川康定626001)
摘要:构造差分,求出了差分的分布函数,讨论了差分的特殊情况:极差的分布函数。并结合均匀分布和指数分布,给出了均匀分布和指数分布下,差分与极差的分布函数。
关键词:差分;极差;分布函数;均匀分布;指数分布
收稿日期:2014-11-20
基金项目:四川民族学院科研项目(XYZB14004)
作者简介:文小波(1986-),男,四川绵阳人,助教,硕士,主要从事Bayes统计方面研究。
中图分类号:O212.1文献标志码:A
1差分的概念
在统计学中,样本来自于总体,样本中含有总体的信息,但所含信息比较分散,为了较好的利用样本中所含的总体信息,需要利用样本构造统计量,次序统计量是一类利用比较广泛的统计量。本文以次序统计量为基础,构造差分与极差,推导出了差分与极差的分布函数,并给出了均匀分布和指数分布的差分与极差的分布函数。
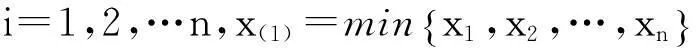
称Z(i)=x(i)-x(i-1)为样本的第i个差分,其中i=1,2,…n.特殊的,称R(n)=x(n)-x(1),为样本极差。
2差分的分布函数
对于一般情况,设总体X的分布函数为F(x),密度函数为f(x)。
定理1Z(i)的分布函数为:
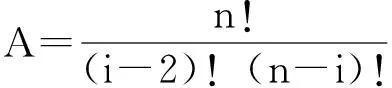
证明:
次序统计量(x(i),x(j)),(i [F(x(j))-F(x(i))]j-i-1·[1-F(x(j))]n-j·f(x(i))·f(x(j)) 其中x(i)≤x(j)[1] 则次序统计量(x(i-1),x(i))的联合分布密度函数为: [F(x(i))-F(x(i-1))]i-(i-1)-1·[1-F(x(i))]n-i·f(x(i))·f(x(i-1)) 整理有 [1-F(x(i))]n-i·f(x(i))·f(x(i-1)) 其中 x(i-1) ≤x(i) 做变换 于是Z(i)与x(i-1)的联合密度函数为: 由此可以算得Z(i)的边际密度为: 则Z(i)的分布函数为: 3极差的分布函数 定理2R(n)的分布函数为: 证明:沿用上文所述符号,则x(1)与x(n)的联合分布密度函数为 做变换,令 则其逆变换为: 其雅可比行列式|J|=1,于是R(n)与x(1)的联合密度函数为: 图2中,D0~SD15是数据地址复用总线,当CMD为高电平访问数据端口,为低电平访问地址端口。DM9000通过EEDCS引脚决定数据位宽,拉高时为8位,拉低时为16位,本文选用16位数据总线模式。DM9000直接接入RJ45网络接口会受到静电串扰,直流干扰等影响网络通信质量。故在DM9000控制器与RJ45中间加入HR601680网络变压器,达到增强信号,降低干扰,提高传输距离的目的[5]。 fRn,Z (x,Z)=n·(n-1)f(Z)·f(x+z)·[F(x+Z)-F(Z)]n-2, 则R(n)的分布函数为: 4均匀分布与指数分布的极差和差分的分布函数 特别的X~U(0,1),时 f(x)=1,0 x~exp(x),f(x)=λe-λx,x≥0,F(x)=1-e-λx,x≥0,[2]。 4.1差分的分布函数 X~U(a,b), X~U(0,1), x~exp(x), 令t=λZ,则 4.2指数分布与均匀分布极差的分布函数 x~exp(λ), X~U(a,b), a 故Z的积分范围为a 对特殊的均匀分布U(0,1)而言,即a=0,b=1,则 FR(n)(x)=nxn-1·(1-x)。 这正是Be(n-1,2)的分布函数,此时Rn~Be(n-1,2) 5结语 构造差分与极差,求证了差分与极差的分布函数,并以指数分布与均匀分布为例,求解了指数分布与均匀分布之下,差分与极差的分布函数,模型可进一步推广到其他分布的情况下。 参考文献: [1]茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社,2011. [2]缪铨生.概率与统计[M].上海:华东师范大学出版社,2007. [3]罗李平.关于极差分布的求法[J].衡阳师范学院学报,2000,12(6):29-31. 责任编辑:程艳艳 Distribution Functions of Difference and Range WEN Xiaobo (Department of Mathematics, Sichuan University for Nationalities, Kangding 626001, China) Abstract:The differential distribution function is obtained by constructing the difference. The differential special case—range distribution function is discussed. Combined with uniform distribution and exponential distribution, the distribution functions of difference and range are given in the condition of uniform distribution and exponential distribution. Keywords:difference; range; distribution function; uniform distributed; exponential distribution