基于光纤传感技术的钢轨变形监测可行性研究

郎向伟，张长生，强小俊

(中国铁道科学研究院深圳研究设计院，广东深圳518034)

基于光纤传感技术的钢轨变形监测可行性研究

郎向伟，张长生，强小俊

(中国铁道科学研究院深圳研究设计院，广东深圳518034)

光纤传感技术与传统的电类、机械类传感技术相比，具有抗电磁干扰能力强、使用方便、易维护等优点。本文探讨其应用于钢轨变形监测的可行性。首先，将两相邻弹性扣件之间钢轨受力形式简化为简支梁，通过理论分析得出钢轨中间点断面同一高度处应变与位移之间的关系;然后将分布式光纤和光栅传感器布设在钢轨简支梁上，通过试验测试数据得到位移与应变的关系，并分析了由应变推算钢轨变形的计算误差。研究结果表明:光纤传感技术在钢轨变形监测上是可行的;光栅传感器测量精度较分布式光纤精度高。研究结果为光纤传感技术在钢轨变形监测中的应用提供了技术支撑。

经典钢轨力学 简支模型 光纤传感技术 钢轨变形监测

光纤传感技术是工程监测领域近几年发展起来的新技术，与传统的电类和机械类传感器相比，具有抗电磁干扰能力强、耐腐蚀、质量轻、体积小、可远距离监测与传输、使用寿命长、在使用期限内维修费用低等优点［1-2］。它可以用来传输多种物理量，具有良好的可靠性和耐久性，适合工程长期监测。目前光纤传感技术在工程结构监测和电力监测等领域得到一些应用。

及时准确地掌握钢轨的变形对运营安全具有重要意义。鉴于光纤传感器在监测方面的优点，本文对钢轨简化计算模型进行理论分析，进行室内钢轨简化模型试验，研究光纤传感技术在钢轨变形监测的可行性。

1 钢轨受力模型

经典钢轨力学方法是将钢轨假定为梁，建立弹性点支撑梁和连续支撑梁模型［3］。作用于钢轨上的外力，包括垂直于钢轨的列车轴重p、正交于钢轨的横向压力和沿钢轨纵轴方向的轴向力三种［4］。为简化计算，主要分析列车轴重产生的垂向力引起的垂直变形，此处取相邻两个弹性扣件之间的钢轨进行简化分析，近似于简支梁模型，见图1。

据材料力学可知，等截面钢轨在载荷作用下的应变ε为［5］

图1 钢轨简支模型

式中:E为钢轨弹性模量;h为钢轨上应变测量点距中性面的垂直距离;x表示测量点在钢轨水平方向上的位置;I表示钢轨x位置处截面惯性矩。设yx=y(x)为钢轨挠曲线，且钢轨向下弯曲时数值为正，M(x)为x点钢轨弯矩，则M(x)可由下式求得［6］

式中，k为轨道系统特性参数，其值一般在0.009～0.020 cm－1。将式(2)代入式(1)可得

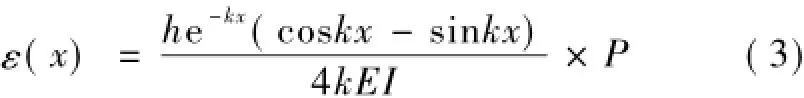
简支作用下等截面梁挠曲线微分方程为

图1中x点处挠曲线微分方程为

将挠曲线方程进行两次积分可得

根据边界条件x=0，y=0和x=l，y=0，可以求出简支结构挠度yx为

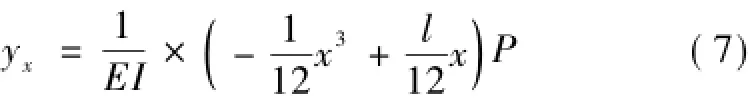
联合式(3)和式(7)可知，当x确定时

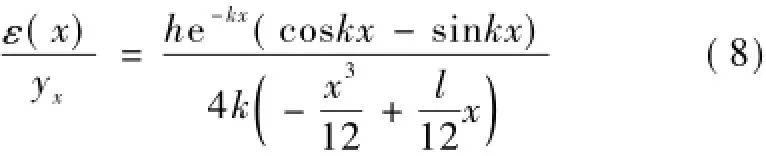
当等截面简支钢轨中x和h确定时，应变与挠度成比例关系。由于目前未有合适的计算方法准确计算出应变与位移的系数，不能将钢轨纵向应变量转化为精确的挠度值。考虑利用统计分析方法拟合出钢轨中确定位置应变与位移的关系，根据拟合系数推算钢轨挠度。

2 光纤传感技术测量原理

目前光纤光栅传感技术主要集中在分布式光纤和光栅传感设备两方面，其中分布式光纤适用于长距离测量，光栅传感设备适用于单点测量。

基于BOTDA的分布式光纤传感技术(图2)原理为:在传感光纤两端分别入射短脉冲光与连续探测光，当两者的频差与光纤中某区域的布里渊频移相等时，则在该区域就会产生受激布里渊(SBS)放大效应，两光束之间发生能量转移［2］。由于布里渊频移与温度、应变存在线性关系，因此在对两激光器的频率进行连续调节的同时，通过检测从光纤一端耦合出来的探测光，就可以确定光纤各小段区域上能量转移达到最大时所对应的频率差，从而得到传感光纤上温度和应变信息，实现分布式测量。BOTDA系统优点为:利用受激布里渊效应，使得接收信号强度大，测量精度高，可实现的动态范围大，便于实现。

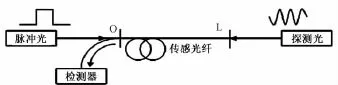
图2 基于BOTDA的分布式光纤传感技术构成

光栅传感技术中布拉格光栅是一种全光纤无源器件，用光纤布拉格光栅作敏感元件的功能型光纤传感器，基于布里渊散射原理的布里渊光时域反射传感器原理［7］:当入射端射入一强且窄的光脉冲时，光纤内部的应变不均匀分布会导致布里渊散射光的频率飘移，由于布里渊散射受温度和应变的影响，因此通过测量布里渊散射的分布便可以得到温度和应变分布信息(图3)。

图3 光纤光栅应变、温度传感机理

分布式光纤所测频率和光栅传感设备所测波长最直接的计算结果是应变，该应变量由外力和温度共同作用引起，对所测数据进行温度补偿后的应变即为外力引起应变。

3 室内钢轨简支模型试验

3.1 试验方法

制作钢轨简支支架，在钢轨轨腰与轨头和钢轨与轨底交界处对称布设光纤和光栅传感器(FBG)，在光栅传感器位置布设百分表。试验分10级加载，每级加载变形量为5 mm，试验中在同一级加载之后，分别读取分布式光纤、光栅传感器(FBG)和百分表的读数，将不同加载级别下读数进行对比分析来确定光纤用于钢轨测量的可行性。钢轨简支试验模型见图4。

图4 钢轨简支试验模型

3.2 试验数据分析

1)钢轨轨腰与轨头分布式光纤数据

实测轨腰与轨头分布式光纤在简支钢轨中间点位移及应变数据见表1。对位移—应变关系曲线进行线性拟合，拟合公式为y=9.117 4x－14.648 0(y表示应变，x表示位移)，根据拟合公式和实测应变，推算位移误差范围为－12%～15%。

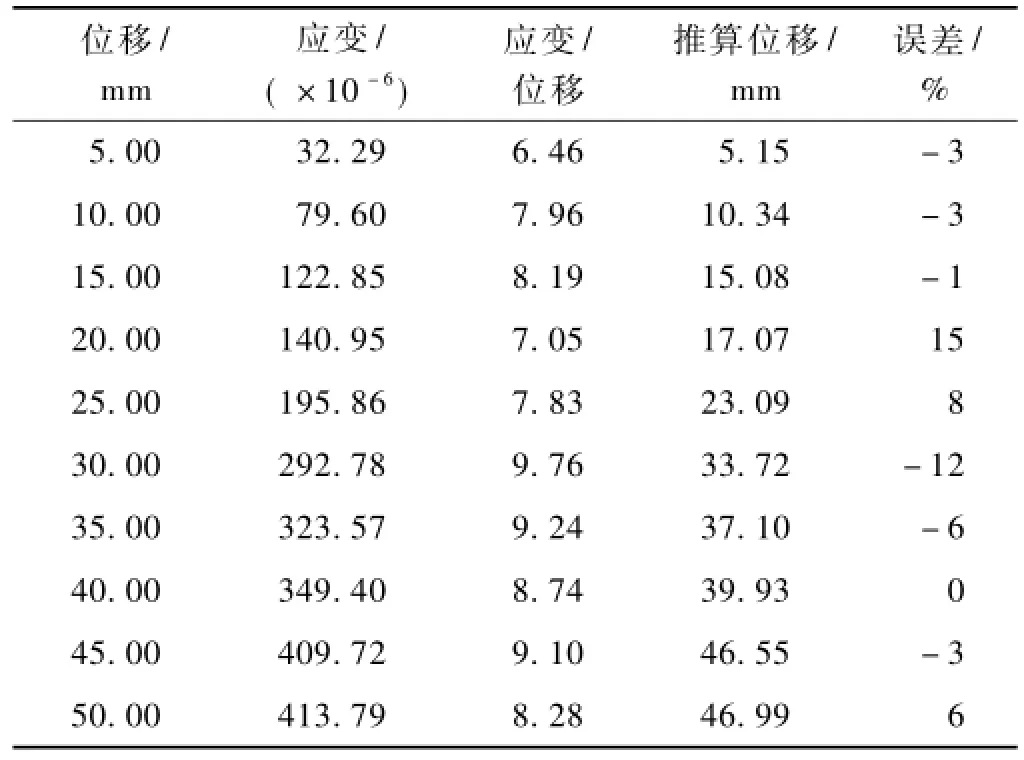
表1 轨腰与轨头位置分布式光纤位移与应变

2)轨腰与轨头光栅传感器数据

实测轨腰与轨头位置光栅传感器(FBG)位移—应变数据见表2。

表2 轨腰与轨头位置光栅传感器位移与应变

对位移—应kkkk变关系曲线进行线性拟合，拟合公式为y=6.294 6x－10.175 0，由于第1级加载数据是在初始布设光纤基础上进行分析的，布设光纤可能存在预张拉未达到线性度最优阶段，在第1级加载数据基础上进行分析，推算位移误差范围为－4%～5%。

3)轨腰与轨底位置分布式光纤数据

实测钢轨轨腰与轨底位置分布式光纤位移—应变数据见表3。

对位移—应变关系曲线进行线性拟合，拟合公式为y=－7.555 0x－6.402 9。根据拟合公式和实测应变，在第1级加载基础上，推算位移误差范围为－9%～6%。

4)轨腰与轨底位置光栅传感器数据

实测钢轨轨腰与轨底位置光栅传感器(FBG)位移—应变数据见表4。

对位移—应变关系曲线进行线性拟合，拟合公式为y=－6.618 9x－6.654 3，根据拟合公式和实测应变，在第1级加载基础上，推算位移误差范围为－5%～3%。

在第1级加载基础上对以上4点试验数据进行分析，布设在钢轨轨腰与轨头的分布式光纤数据拟合之后由应变反算位移误差为－12%～15%，在该位置的光栅传感器由应变反算位移误差为－4%～5%;布设在钢轨轨腰与轨底的分布式光纤拟合之后由应变反算位移误差为－9%～6%，在该位置布设的光栅传感器由应变反算位移误差为－5%～3%，试验数据表明:

1)试验中每级分布式光纤、光栅传感器和百分表所测数据确定的应变/位移值在一定范围之内，在第1组采集数据基础上分析，轨腰与轨头位置分布式光纤系数为7.05～9.76，光栅传感器系数为5.16～6.17，轨腰与轨底位置分布式光纤系数为－7.32～－8.63，光栅传感器系数为－6.53～－7.42，分布式光纤和光栅传感器根据拟合系数由应变推算位移误差较小，表明分布式光纤和光栅传感器在钢轨变形测量方面具有可行性。

表3 轨腰与轨底位置分布式光纤位移与应变

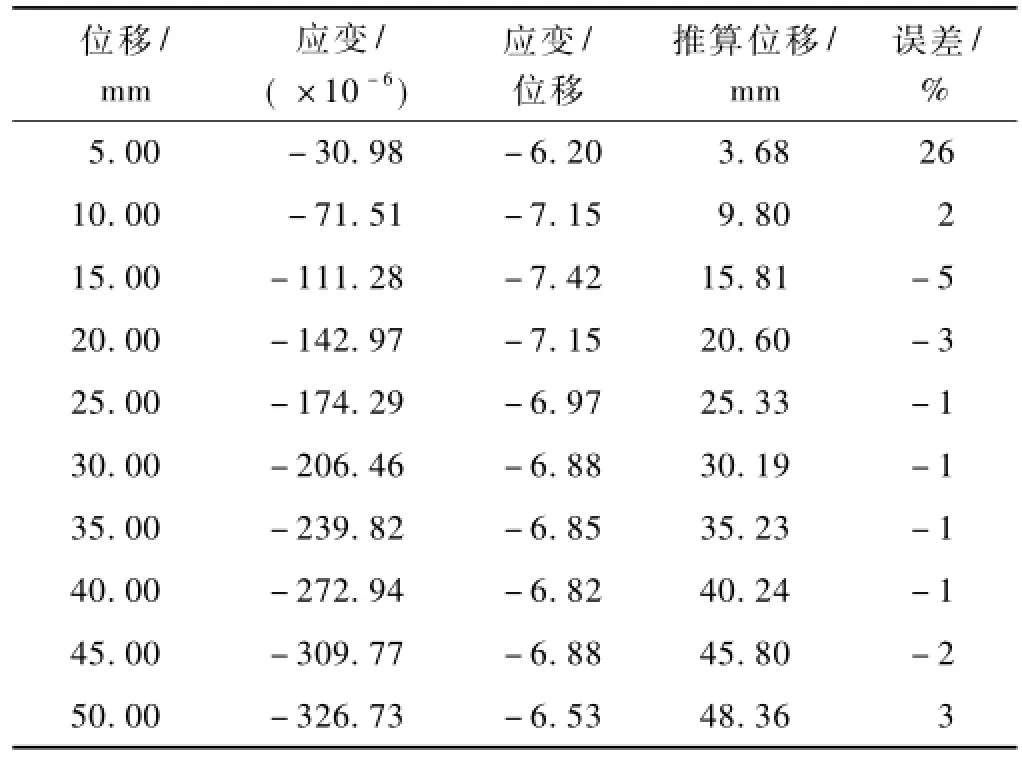
表4 轨腰与轨底位置光栅传感器位移与应变

2)光栅传感器所测精度高于分布式光纤数据，其原因为分布式光纤解调仪精度(20×10－6)低于光栅传感器精度(2×10－6)。由于分布式光纤在长距离监测上具有易于实现和成本较光栅传感器低等优势，以后将光纤传感技术应用于钢轨变形监测时，可将分布式光纤作为定性手段对长距离线路进行普查，在发现问题部位重点布设光栅位移传感器进行精确测量。

3)光纤布设在轨腰与轨底较轨腰与轨头部位测量更精确，原因可能为固定轨腰与轨头位置光纤传感器胶水流动性较轨腰与轨底高，影响传感器粘贴效果和协调变形性能。

4 结论

1)忽略正交于钢轨的横向压力及沿钢轨纵轴方向的轴向力，主要考虑垂直于钢轨的列车轴重荷载，将两相邻弹性扣件间钢轨假定为简支梁模型进行分析，等截面钢轨同一位置处应变和位移成比例关系。

2)对钢轨简支模型布设光纤传感器进行试验，试验数据表明分布式光纤和光栅传感器在钢轨变形监测上具有可行性，其中光栅传感器测量精度较分布式光纤精度高，布设在轨腰与轨底光纤和光栅传感器精度优于布设在轨腰与轨头。

3)目前尚无合适的计算方法将钢轨纵向应变量精确转化为竖向挠度，以后将光纤传感技术应用于钢轨变形监测时，可考虑将分布式光纤作为定性手段对长距离线路进行监测，在应变量较大部位重点布设光栅位移传感器进行精确变形测量。

［1］李东侠．钢轨断裂原因分析及防治措施［J］．铁道工务，2005 (3):67-69．

［2］张竞文，吕安强，李宝罡，等．基于BOTDA的分布式光纤传感技术研究进展［J］．光通信研究，2010(4):25-28．

［3］陈伯靖，钱小益，秦超红，等．铁路钢轨受力分析模型比较研究［J］．工程力学，2013，30(6):93-97．

［4］米皓坤，骆妍，梁磊，等．弹性约束下无缝钢轨受力形变规律研究［J］．武汉大学学报(工学版)，2013，46(4):499-523．

［5］孙训方，方孝淑，关来泰，等．材料力学［M］．北京:高等教育出版社，2002．

［6］YAN L S，ZHANG Z T，WANG P，et al．Fiber Sensors for Strain MeasurementsandAxleCountinginHigh-speedRailway Applications［J］．IEEE Sensors Journal，2011，11(7):1587-1594．

［7］李川，张以漠，赵永贵，等．光纤光栅原理、技术与传感应用［M］．北京:科学出版社，2005:199-207．

Feasibility study on rail deformation monitoring based on optical fiber sensing technology

LANG Xiangwei，ZHANG Changsheng，QIANG Xiaojun
(Shenzhen Research and Design Institute，China Academy of Railway Sciences，Shenzhen Guangdong 518034，China)

Comparedwiththe traditional electrical andmechanical sensingtechnology，optical fibersensing technology has the advantages ofstronganti electromagnetic interferenceability，easyuseandconvenient maintenance．In this paper，its feasibility applied in rail deformation monitoring was discussed．T he rail stress form between two adjacent elastic fastenings can be simplified as a simply supported beam and the relation between displacement and strain in the same height position of simply supported rail middle section is concluded by theoretical analysis，by setting the distributed optical fiber and grating sensors on the rail simply supported beam the relation between displacement and strain is obtained by test data and the calculation error of rail deformation deduced by strain is analyzed．T he research results showed that the fiber sensing technology is feasible for rail deformation monitoring and grating sensor measurement accuracy is higher than distributed optical fiber precision，which could provide a technical support for optical fiber sensing technology applied in rail deformation monitoring．

Classical rail mechanics;Simply supported model;Optical fiber sensing technology;Rail deformation monitoring

U213.2+13

A

10．3969/j．issn．1003-1995．2015．03．34

1003-1995(2015)03-0122-04

(责任审编李付军)

2014-07-11;

2014-09-20

中国铁道科学研究院院基金(SZY201205)

郎向伟(1985—)，男，河南舞阳人，助理研究员，硕士。