近小尺度壁面水下爆炸射流特性数值模拟*

卢　熹,王树山,马　峰,徐　锐

(北京理工大学爆炸科学与技术国家重点实验室,北京　100081)

近小尺度壁面水下爆炸射流特性数值模拟*

卢熹,王树山,马峰,徐锐

(北京理工大学爆炸科学与技术国家重点实验室,北京100081)

摘要:为了考察结构尺度对气泡射流动态特性的影响,利用AUTODYN软件,针对三种不同尺度的球形固壁面进行近壁面水下爆炸数值模拟计算。计算结果表明:壁面尺度越小,射流穿透气泡越早,气泡体积越小、越细长,射流速度越大,但射流宽度越小,射流冲击压力对壁面的作用越弱,压力产生的比冲量越小。研究结果初步揭示了结构尺度的减小不利于水射流威力的发挥,为打击小型目标的水中兵器战斗部威力设计提供有益参考。

关键词:水下爆炸;气泡;水射流;球形固壁面;AUTODYN数值模拟

0引言

装药在水下爆炸是水中兵器对目标毁伤的主要手段,其能量以冲击波能和气泡能的形式向外释放。气泡能在向水中传递能量的过程中形成气泡脉动并引起脉动压力和滞后水流,当气泡在结构表面附近振荡时,气泡会在坍塌阶段受Bjerknes力的作用形成指向结构表面的高速水射流,可能造成结构的局部损伤。水射流使气泡能对结构的作用更集中,因此,有效利用水射流可有助于提高水中兵器对目标的毁伤威力。国内外对近壁面的气泡射流形成过程开展了较多的实验与数值模拟研究[1-4],在射流形成条件及影响规律等问题上取得了很多成果。但研究采用的结构大都局限于一些简单的平板结构,且结构的尺度较大,多以爆炸气泡与海底或大型舰艇的相互作用为背景。然而,随着“网络中心战”作战模式的逐步发展,未来水中兵器的作战目标将发生深刻的变化,除了舰艇平台以外,还需要高效打击水下信息节点或武器节点等小型目标[5],如水下浮标、水雷等。在这种背景下,小尺度结构对气泡射流形成的影响成为需要考虑的问题。为此,文中利用AUTODYN软件,针对三种不同尺度的球形固壁面进行近壁面水下爆炸气泡动态特性数值模拟研究,分析了结构尺度对气泡射流动态特性的影响。

1计算模型

1.1　模型描述

建立二维轴对称模型,如图1所示。采用1.28 g球形TNT炸药,炸药密度为1 630 kg/m3,采用中心起爆方式。二维水域尺寸为12 m×6 m,定义为Euler单元,气泡与壁面作用区域网格加密,最小单元尺寸为2.5 mm。由于水域尺寸很大,水域边界对气泡脉动的影响可以忽略,因此,水域未施加边界条件,此时相当于刚性边界。忽略浮力对气泡的作用,整个水域均匀定义10 m水深的静压力。由于网格尺寸较大,为保证填充药量精度,利用AUTODYN提供的映射功能,先在一维球对称模型中计算炸药起爆和冲击波的传播,在爆轰产物膨胀且冲击波未达到壁面时,将计算结果映射到二维轴对称模型中继续计算。壁面采用球形结构,采用Lagrange单元,壁面边界施加固定约束边界条件从而实现刚性固定壁面。壁面与Euler单元之间定义流固耦合。

图1　计算模型

1.2　炸药的状态方程

TNT爆轰产物中的压力用JWL状态方程描述:

(1)

式中:E为单位质量内能;V为爆轰产物相对比容;A、B、R1、R2和ω为常数。状态方程各参数取值[6]为:A=3.71×108kPa,B=3.23×106kPa,R1=4.15,R2=0.95,ω=0.3,E=7.0×106kJ/m3。

1.3　水的状态方程

水的状态方程采用多项式状态方程,当水受压时(μ>0),其状态方程为:

(2)

当水受拉或空化时(μ<0),其状态方程为:

(3)

式中:A1、A2、A3、B0、B1、T1和T2为常数;μ=ρ/ρ0-1,ρ为水的密度,ρ0为水的初始密度;e为水的比内能,e=(ρgh+P0)/(ρ·B0);h为水深;P0为大气压力。水的状态方程各参数取值为:A1=2.20×106kPa,A2=9.54×106kPa,A3=1.46×107kPa,B0=0.28,B1=0.28,T1=2.20×106kPa,T2=0 kPa,ρ0=1 000kg/m3,e=711.875 J/kg。

2结果与分析

2.1　结果有效性验证

为了验证计算结果的精度,将模型在自由场中计算得到的部分特征量与经验值进行比较,如表1、表2所示。其中,冲击波压力峰值[7]、脉动压力峰值[8]、气泡最大半径和脉动周期[9]分别利用经验式(4)～式(7)计算得到。

(4)

式中:Pm为冲击波峰值压力(Pa);W为TNT装药质量(kg);r为爆心到测点的距离(m);r0为装药半径(m)。

(5)

式中:Pmax为二次压力波峰值压力(MPa);P0为爆炸深度静水压力(MPa);W为TNT装药质量(kg);r为爆距(m)。

(6)

(7)

对于TNT炸药KR=30,KT=0.295,h为炸药所在水深(m);W为装药量(kg)。

从表1可以看出,与经验值相比,爆炸场中不同爆距上的冲击波峰值压力误差过大,而二次压力峰值误差较小,这是由于模型网格密度较低,在与数值粘性的共同影响下,高频冲击波峰值被抹平,且衰减较快,但对低频的二次压力波峰值的影响则较小。从表2可以看出,气泡最大半径和脉动周期的计算值与经验值非常接近,说明模型能较精确模拟气泡脉动过程的水介质流动。

表1　冲击波与二次压力峰值的计算值与经验值对比

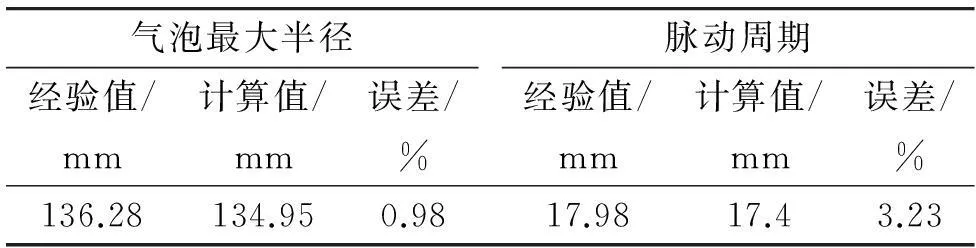
表2　 气泡第1次脉动最大半径与脉动周期的计算值与

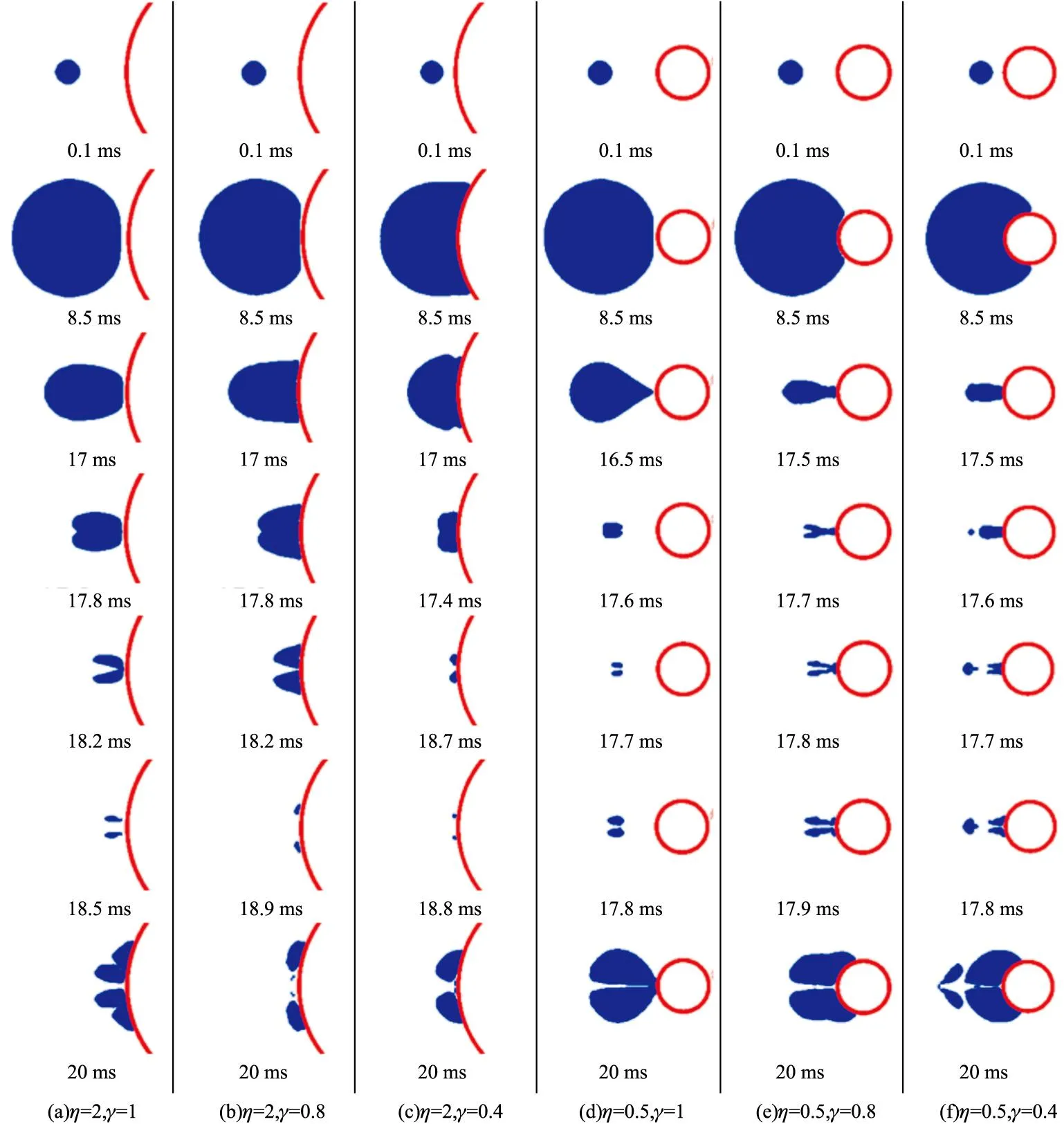
图2　气泡演变过程

2.2　气泡形态演变过程

为了考察壁面尺度对气泡射流形成的影响,模型采用了三种不同尺度的球形壁面,每种壁面下设置4个起爆距离。定义球形壁面的半径R与气泡最大半径rmax的比值为壁面尺度参数η,即η=R/rmax;定义爆心距壁面最近距离L与气泡最大半径rmax的比值为距离参数γ,即γ=L/rmax。取rmax=135 mm,采用的壁面尺度参数分别为η=2,1,0.5,距离参数分别为γ=1,0.8,0.6,0.4。

部分工况下气泡形态演变过程如图2所示。对于壁面η=2,当γ=1时,气泡在膨胀阶段受壁面阻碍,近壁面气泡边界变得扁平。当气泡侧边界和远壁面边界开始收缩时,近壁面边界仍然向壁面缓慢扩张,表现为气泡整体向壁面的移动。由于远壁面收缩速度较快,且沿着边界存在速度梯度,越靠近对称轴的边界速度越大,使得远壁面边界逐渐向气泡内凹陷,形成指向壁面的锥形射流。18.2 ms时,射流穿透气泡并立刻冲击壁面,冲击水流沿着壁面向四周流动,气泡变为环状继续收缩,18.5 ms时,环状气泡体积达到最小随后开始二次膨胀。γ=0.8时,气泡在膨胀阶段贴附于壁面,而在收缩阶段始终吸附于壁面上。γ=0.4时,贴壁面的气泡侧边界较快收缩,气泡呈蘑菇状。

比较3个距离参数下气泡形态演变过程可以发现,随着距离减小,射流穿透气泡时的气泡体积先增大后减小。这主要与气泡边界收缩的速度分布有关。当距离较大时,气泡近壁面边界仍有较快的收缩速度,使得气泡整体收缩速度较快。而随着距离减小,气泡贴附于壁面导致收缩速度变慢,气泡整体收缩速度也因此变慢。当距离进一步减小,气泡远壁面边界收缩速度分布的梯度变小,射流形成较晚,使得射流形成时气泡的体积更小。

在气泡收缩时,向气泡流动的水流在壁面的边缘处形成绕流,使得壁面边缘流速加快,进而对气泡侧边界收缩形态产生影响。壁面尺寸越小,绕流的影响越明显。对于壁面尺度参数η=0.5,当距离参数为1时,绕流使近壁面气泡边界变为锥形,锥顶部逐渐脱离壁面(16.5 ms),气泡呈水滴状。同时,绕流水流在对称轴处汇聚,使气泡锥顶收缩速度突然加快,锥顶处发生凹陷并形成背离壁面方向的射流(17.6 ms)。而远壁面边界此时也形成指向壁面方向的射流。由于远壁面射流的冲量更大,两股射流相撞后,形成指向壁面方向的冲击水流。当γ=0.8时,气泡仍贴附于壁面,但受壁面绕流的作用,气泡侧边界收缩较快,气泡变得细长,射流在气泡开始膨胀后穿透气泡。当γ=0.4时,细长气泡出现颈缩,最终分成两段(17.6 ms),近壁面气泡仍形成指向壁面的射流,远壁面气泡形成背离壁面方向的射流。

2.3　射流顶端速度与宽度

为了讨论射流速度特性,图3给出了各工况下气泡边界距壁面最远点的速度历史曲线,在射流形成后该点速度为射流顶端速度。从图中可以看出,在壁面尺度参数η=2时,各曲线趋势一致。随着气泡收缩,边界速度增加,且增加趋势不断加快,达到一定值后,曲线变得平缓。由气泡演化过程可知,曲线平缓段对应于射流形成到穿透气泡的过程,曲线末端为射流穿透气泡时的射流顶端速度。由此可知,射流初始速度主要在凹陷射流形成前气泡整体的收缩阶段获得,射流在气泡内穿行过程的速度变化幅值较小。比较不同距离曲线可以看出,距离越小,射流速度越小,射流穿透气泡越晚。

对于η=1,从图中可以看到,当距离参数较大时,曲线的趋势与η=2的各工况类似,而当γ=0.4,射流顶端速度变大,这是由于距离较近,壁面边缘的绕流使气泡远壁面收缩速度加快。

对于η=0.5,射流速度变化更加复杂。由于射流几乎在气泡膨胀阶段穿透气泡,气泡内部压力升高,导致射流穿过气泡的速度衰减较快。在γ=1时,受绕流影响,气泡形成两股射流对撞,导致最终射流穿透速度降低。γ=0.4时,速度曲线起始于气泡被切断时刻,射流速度主要受绕流作用影响。

绕流使流动向中部汇聚,增加了射流的速度。比较不同壁面尺度下的速度曲线可知,壁面尺寸越小,射流速度越高,射流穿透气泡越早。

在锥形射流冲击壁面的过程中,射流后部的推进使壁面受到的冲击面积有所增加,同时环形气泡内径随之扩大,因此,以射流冲击壁面后环形气泡达到的最大内径表征射流宽度,用来讨论射流对壁面冲击面积的影响。不同壁面尺度参数下射流宽度随距离参数变化的曲线如图4所示,可以看出,壁面尺度越小,射流宽度越小。同一壁面尺度下,随着距离减小,射流宽度先增大再减小。

图3　气泡远壁面边界点速度历史

图4　射流宽度随距离参数的变化

2.4　射流冲击压力和比冲量

为了讨论射流对壁面的作用,提取了各工况下在射流冲击壁面阶段距壁面中心5 mm处的压力曲线如图5所示。分析各工况下的曲线特征可知,曲线记录了三种类型的压力信息,即气泡内爆轰产物压力、射流冲击压力以及环形气泡脉动压力。曲线前段比较光滑,此时气泡紧靠壁面,曲线压力为气泡内部爆轰产物的压力;随后出现的具有高频大幅振荡特征的压力为射流冲击壁面引起的冲击压力;随着冲击压力振幅的衰减,压力值整体上升,形成持续时间较长的波峰,这是环形气泡再次膨胀时产生的脉动压力。

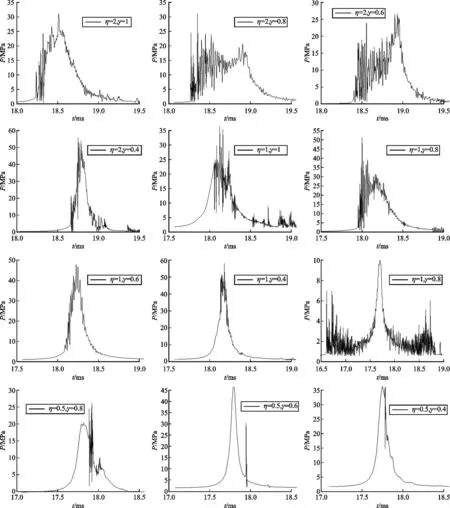
图5　壁面附近压力历史

\水流冲击作用与气泡内部压力或脉动压力相互叠加。当冲击射流形成早,环形气泡仍有较长时间的收缩过程,冲击压力明显先于脉动压力,如工况η=2,γ=0.8，0.6所示。当气泡收缩较小,气泡内部压力上升,此时射流冲击壁面,冲击压力与脉动压力叠加。在工况η=2,γ=1，0.4以及η=1,γ=0.8，0.6中,冲击压力叠加于脉动压力的上升沿;而在工况η=1,γ=1，0.4中,冲击压力叠加于脉动压力的波峰处。当射流形成于气泡的膨胀阶段,气泡内部压力首先形成波峰,并在压力的下降沿出现短暂的射流冲击压力,此时曲线上没有脉动压力,如工况η=0.5,γ=0.8，0.6，0.4所示。对于工况η=0.5,γ=1,脉动压力波形前后出现两次水流冲击压力,由气泡演变过程可知,前期水流冲击压力是由气泡脱离壁面时绕流在壁面中部的汇聚造成的,而后期压力为射流冲击。由于经历了两股射流对撞以及流体衰减作用,射流冲击能力已大幅下降,其压力幅值稍小于前期水流冲击。

综合分析各工况的压力曲线特征可知,当壁面尺度较小时,绕流作用对气泡影响较大,气泡收缩较快,气泡内部压力对壁面作用显著;当壁面尺度较大时,Bjerknes力的作用对气泡影响较大,射流冲击与脉动压力作用显著,并且壁面尺度越大,射流冲击对壁面作用越显著。

同一壁面尺度参数下,压力曲线中的最大峰值压力随着距离减小而增大。而距离参数γ=0.8时的冲击压力峰值均大于脉动压力或气泡内压力峰值,说明该距离参数范围内射流冲击作用较强。相同距离参数下,η=1工况下的最大峰值压力较大,这是由于该壁面尺度参数下冲击压力在脉动压力波峰附近叠加造成的。

压力峰值不能完全反映压力对壁面的作用,还应该考察压力产生的比冲量。比冲量可通过对压力曲线在时间上的积分得到,图6为不同壁面尺度参数下比冲量随距离参数的变化。从图中可以看出,壁面尺度越大,比冲量越大,且壁面尺度越大,不同壁面尺度下的比冲量差距越小。同一壁面尺度下,对于η=0.5的工况,此时气泡内部压力作用显著,比冲量随着距离参数增加而减小。而η=1，2工况的比冲量随着距离参数增加先增大再减小,比冲量最大值在距离参数γ=0.8附近。比较η=1，2的曲线可知,在上升阶段比冲量差距较小,而在减小阶段差距增大。

图6　比冲量随距离参数的变化

3结论

为了考察结构尺度对气泡射流动态特性的影响,文中利用AUTODYN软件,针对三种不同尺度的球形固壁面进行水下爆炸数值模拟计算。通过对计算结果分析,获得以下结论:

1)气泡收缩时水流经过小尺度壁面形成的绕流对水射流特性产生显著影响。随着壁面尺度的减小,气泡形态会变得更为细长,并且容易发生颈缩而分离为两个气泡。

2)射流速度的大小主要形成于射流出现前的气泡收缩阶段,射流在气泡内运动过程中速度变化幅度较小。壁面尺度越小,射流速度越大,射流穿透气泡越早,射流宽度越小。壁面尺度较大时,射流速度随距离参数的减小而减小,射流宽度先增大后减小;壁面尺度较小,绕流作用增强,射流速度会在较小距离参数下变大。

3)壁面受到射流冲击压力与气泡内部压力或环形气泡脉动压力的叠加作用。压力产生的比冲量,随壁面尺度增大而增大,且壁面尺度越大,不同壁面尺度下比冲量的差距越小。当壁面尺度较小时,气泡内部压力对壁面作用显著。此时,产生的比冲量随着距离参数增加而减小。当壁面尺度较大时,射流冲击与脉动压力作用显著,并且壁面尺度越大,射流冲击对壁面作用越显著,此时,压力产生的比冲量随着距离参数增加先增大再减小。

参考文献:

[1]Blake J R, Taib B B, Doherty G. Transient cavities near boundaries, Part I: Rigid boundary [J]. Journal of Fluid Mechanies, 1986, 170: 479-497.

[2]Klaseboer E, Hung K C, Wang C, et al. Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure [J]. J Fluid Mech, 2005, 537: 387-413.

[3]Zhang A M, Yao X L, Fen L H. The dynamic behavior of a gas bubble near a wall [J]. Ocean Engineering, 2009, 36: 295-305.

[4]崔杰, 张阿漫, 郭君, 等. 舱段结构在气泡射流作用下的毁伤效果 [J]. 爆炸与冲击, 2012, 32(4): 355-361.

[5]王树山, 卢熹, 马峰, 等. 鱼雷引战配合问题探讨 [J]. 鱼雷技术, 2013, 21(3): 224-229.

[6]Lee E, Finger M, Collins W. JWL equations of state coefficients for high explosives, UCID-16189 [R]. 1973.

[7]Zamyshlyayev B V. Dynamic loads in underwater explosion, AD-757183 [R]. 1973.

[8]P. 库尔. 水下爆炸 [M]. 罗耀杰, 等译. 北京: 国防工业出版社, 1960.

[9]松佐夫 H H. 水下及空中爆炸理论基础 [M]. 王华, 林时干, 译. 北京: 国防工业出版社, 1965.

收稿日期:2014-05-20

作者简介:卢熹(1983-),男,辽宁锦州人,博士研究生,研究方向:爆炸力学。

中图分类号:O382.1

文献标志码:A

Numerical Study on Characteristics of Underwater Explosion Jet
Near Small Scale Wall

LU Xi,WANG Shushan,MA Feng,XU Rui

(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)

Abstract:For investigating influence of structure scale on dynamic characteristics of water jet, numerical simulation of underwater explosion near three sizes of spherical wall was carried out. The result shows that the smaller scale of the wall is, the sooner jet penetrates bubble, the smaller and slenderer bubble is, the higher speed of jet is, the smaller width of jet is, the weaker jet impacts the wall, the smaller impulse is. The result preliminarily reveals that the small scale structure can reduce water jet power, which provides a useful reference for warhead design for underwater weapons fighting against small targets.

Keywords:underwater explosion; bubble; water jet; spherical solid boundary; AUTODYN numerical simulation