反坦克导弹末制导稳定性及对精度影响分析*

杨　凯,张建灵,严宪军

(中国兵器工业第203研究所,西安　710065)

反坦克导弹末制导稳定性及对精度影响分析*

杨凯,张建灵,严宪军

(中国兵器工业第203研究所,西安710065)

摘要:文中为了分析导弹末制导稳定性及其对精度的影响,首先研究了比例导引弹道稳定条件,提出了比例导引弹道稳定性设计和分析方法。其次,对直升机载反坦克导弹系统误差源进行分析建模,利用精度分析方法设计出精度分析系统。最后依靠高精度、高准确度的误差源模型及文中设计的精度分析系统进行大量数字仿真试验,得到置信度高的精度分析结果和末制导控制系统考核结果。

关键词:反坦克导弹;比例导引规律;弹道稳定性;精度分析

0引言

未来直升机载反坦克导弹系统应具有:防区外远程精确打击能力;抗干扰、全天候作战能力;“打了不管”的作战能力;多平台发射、攻击多种目标的通用化和多功能作战能力。新型直升机载反坦克导弹系统大都采用复合制导体制,中制导主要采用GPS+组合导航技术,末制导主要采用激光半主动、主/被动毫米波、红外/电视图像等制导体制。

1制导控制系统组成及工作原理

制导控制系统主要包括指令传输装置、导引头、GPS+组合导航系统、制导控制计算机、舵机系统以及信息处理软件等,如图1所示。

导弹离轨后,首先进入初制导段,按照初始段方案弹道飞行,然后进入中制导段,按照预先设计的弹道高度飞行,导弹到达导引头捕获域后,导引头启动,先以一定的模式搜索、扫描目标,确认待攻击的目标后,随即锁定目标并转入自动跟踪状态,此时进入制导控制系统的中末过渡段,导弹平滑过渡到末制导飞行段后,导弹按改进比例导引律飞行,实现对目标的精确打击。

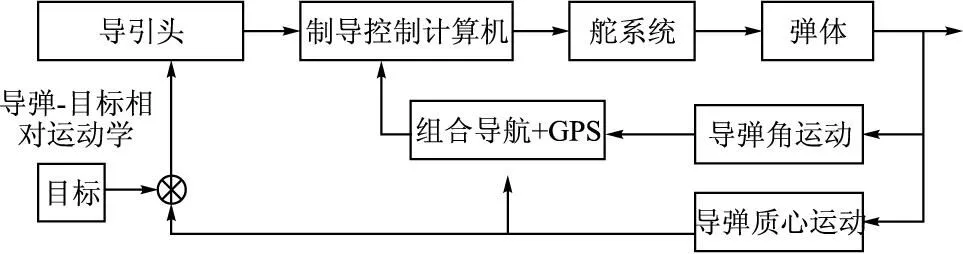
图1　制导控制系统组成框图

2比例导引规律研究

2.1　比例导引规律

比例导引规律是指导弹在攻击目标的导引过程中,导弹速度矢量的旋转角速度与弹目线的旋转角速度成比例的一种导引方法[1]。

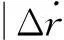
2.2　比例导引弹道稳定条件分析

由于类方形蜂窝是凸六边形蜂窝与凹六边形蜂窝的一种过渡形式，研究不同壁厚类型下其夹芯特有的力学性能及其夹层结构的振动特性显得尤为重要。鉴于此，针对四边简支类方形蜂窝夹层结构，本文在深入对比等壁厚与双壁厚六边形蜂窝夹芯等效弹性参数的基础上，推导类方形蜂窝夹芯的等效弹性参数；同时以蜂窝夹层结构的实际构造为基础，根据类方形蜂窝结构与凸六边形蜂窝结构的相似性，引用蜂窝夹层结构的自由振动方程，采用理论计算与仿真模拟相结合的方法，求解四边简支条件下类方形蜂窝夹层结构的振动特性，同时分析夹芯壁厚、夹芯等效密度及等效剪切模量等对四边简支类方形蜂窝夹层结构固有频率的影响。

1)载机误差:载机速度、高度、离轴角、横滚角、载机振动、载机悬翼下洗流场带来的气动误差等;

其中:N为比例导引回路有效导航比;Ts为比例导引段剩余飞行时间。

可见弹道稳定的充要条件是:比例导引段剩余飞行时间大于某个值;有效导航比大于2而小于某个值。

比例导引弹道稳定性的判断方法为:1)当系统特征方程次数较低时,应用古尔维茨稳定性判据;2)当系统特征方程次数较高时,先采取模型降阶处理,然后应用古尔维茨稳定性判据,或者依靠先进的计算机辅助算法,直接求解特征方程的根[2]。下面给出导弹系统动力学等效为二阶振荡环节时比例导引弹道稳定性条件。

2.3　比例导引弹道稳定性分析

导弹采用比例导引规律飞行时,制导控制系统是一个复杂的时变非线性系统,需要在一定的假设条件下,将制导控制回路简化成线性系统进行分析和设计[5]。线性化后的比例导引回路原理图如图2所示。

图2　比例导引回路原理图

图中:Δr为弹目相对距离;W1(S)为制导滤波器传递函数;Wt(S)为陀螺传递函数;V为导弹飞行速度;W2(S)为阻尼回路传递函数;Wg(S)为重力拢动模型;T1为弹体时间常数;Wp(S)舵机传递函数;Kv为增益补偿信号;K1、K2为导引头回路参数;Wd(S)为弹体传递函数;ym(t)、yd(t)为目标、导弹位置信号。

下面根据比例导引回路原理图,以Δr=3 000 m为例,给出系统稳定性分析方法。

(9.905×10-9×S12+4.361×10-6×S11+8.546×10-4×S10+0.11×S9+9.356×S8+556.9×S7+2.147×104×S65.433×105×S5+5.548×106×S4+2.027×107

(7.876×104×S3+5.997×106×S2+5.64×106×S)/

1)求出闭环系统的传递函数为:

×S3+2.065×107×S2+5.64×106×S)

2)求解系统闭环特征方程,得到系统特征根。

3)由系统特征方程根判定闭环系统稳定性。

新疆地区由于光照时间长，非常适宜棉花生长，是我国的主要棉花种植区。近年来棉花种植面积不断扩大，促进了当地经济的快速发展，但棉秆资源作为一种农业剩余物也给当地的环境造成一定的压力。将棉花秸秆炭化制备成生物炭，并将其施入土壤中，可实现农业资源的高效循环利用。

图3为开环系统波德图、根轨迹图,图4为闭环系统阶跃响应图。

房间的顶是星空以后，刘必芒又突发奇想，说这样，要充分体现这个星空包房的的主题，不光星星是星星，明星也是星星，所以，在墙壁上要贴满明星们的脸的照片，而且要注意剪裁，只要他们的脸，这就能让人彻底感觉这个包厢星光熠熠。

不同弹目距离Δr下系统特性如表1所示,由表1可见,随着弹目距离的减小,比例导引回路增益变大,系统响应速度加快,系统带宽增加,稳定裕度不断减小,当导弹接近目标到一定程度后,系统特征方程的特征根出现正根或正实部时,系统开始失稳,随着弹目距离越来越小,正根或正实部越来越大,系统发散越快。

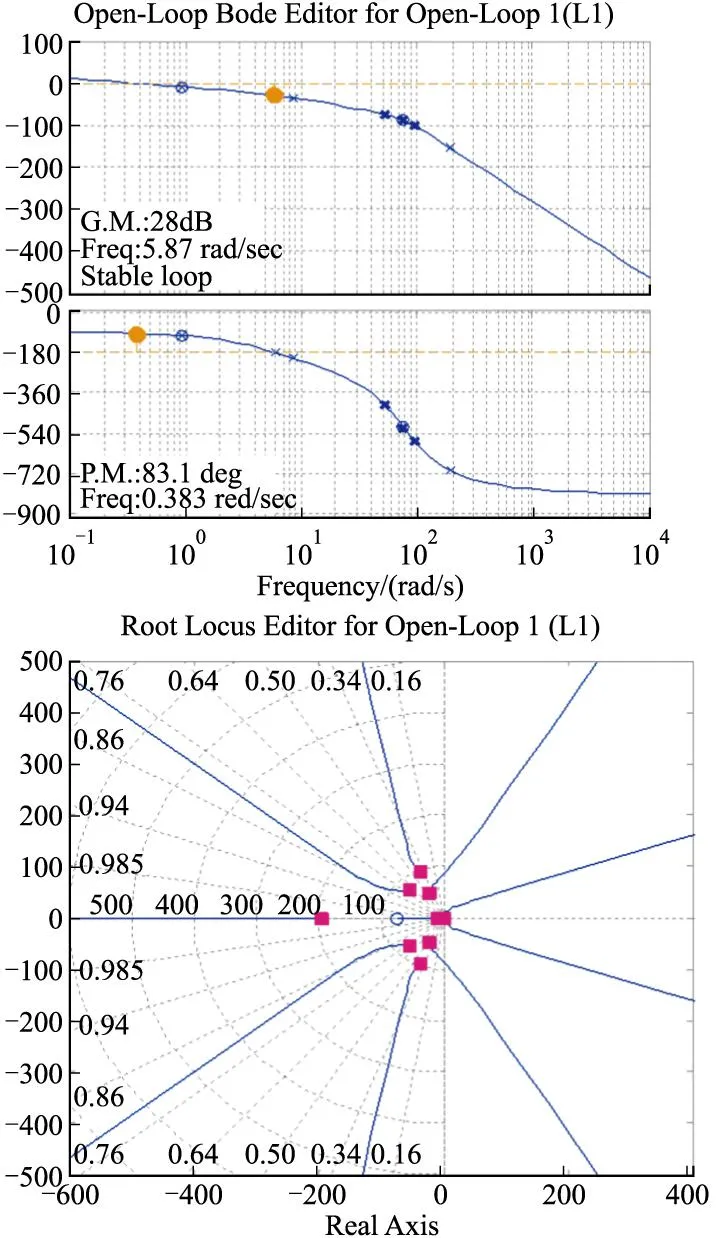
图3　开环系统波德图、根轨迹图

Δr/m幅值裕度h/dB相角裕度γ/(°)截止频率ωc/(rad/s)带宽ωb/Hz特征方程根系统稳定性300028.083.10.3830.0698-4.80,-0.95,-0.44稳定200024.579.70.5740.113-4.22,-0.95,-0.74稳定100018.569.81.130.284-2.13±1.12i,-0.95稳定100-1.51-6.546.461.5-0.95,0.27±6.27i不稳定

图4　闭环系统阶跃响应图

3精度分析系统研究

3.1　精度分析法

导弹制导控制系统是一个复杂非线性时变系统,目前进行制导控制系统精度分析以及考核武器系统总体部门提出的战术技术指标时,通常采用蒙特卡洛试验法[3],该方法是唯一的不需要模型简化的统计分析方法。

杨先生又喑了，只发了狠地吃烟。我和大梁都呆呆地望着他，等他言声。这厢静得出奇，隔壁学童的读书声就变得更响亮了——

3.2　精度分析系统结构

干扰弹道模块:主要计算导弹在受到各种干扰条件下的飞行速度、轨迹、命中精度等参数。

IBM开发的Fabric[6]看到了另外一个生存空间，那就是避开以太坊，构造联盟链，在企业中运行。得益于IBM的代码质量和一贯良好的形象，Fabric很快在联盟链中占据了主导地位。Fabric的特点是不用密码货币，转而用节点背书，其中每个节点的身份可以识别，不诚实的节点需要付出代价。目前在大部分所谓落地的应用中，例如：银行、供应链、积分、税务等场景，无一例外地采用了联盟链的模式。

标准弹道模块:主要计算导弹在理想条件下的飞行速度、轨迹、命中精度等参数。

设计精度分析系统,首先根据导弹飞行原理和控制原理建立导弹六自由度飞行数学模型,再根据发射条件、干扰因素等建立干扰模型,最后通过精度分析统计方法建立精度分析模块。因此精度分析系统包括标准弹道模块、干扰弹道模块和精度分析模块三部分。各模块的功能和作用分别为:

在全局路径规划过程中需选取合适的适应度函数，即将目标函数作为评价群体中路径优劣的标准和依据。[6]适应度函数的建立应综合考虑安全性与经济性，需满足以下条件：与障碍物无干涉、路径长度尽可能短和各转向角要尽可能小。这里综合考虑3个条件作为适应度函数的评价标准。

精度分析模块:对标准弹道计算结果与干扰弹道计算结果进行统计分析,计算出导弹落点的方差和均值,以及导弹命中概率、圆概率误差等精度分析的相关数据。

3.3　系统误差源分析

误差源模型的准确性直接影响到武器系统精度分析的准确性,因此首先要对系统的主要误差源及误差源的分布规律进行分析建模[6]。对于直升机载反坦克导弹来说,考虑的主要误差源有:

平台主要实现对当前互联网上各种数字资源的获取、编目和管理，特别针对各种不同的数据资源的特点、面向移动设备的最新发展以及人们阅读习惯的改变，构建面向移动互联网的新型阅读系统，提高读者的阅读体验。

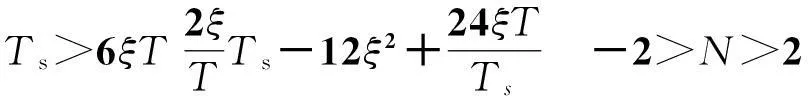
5)环境因素误差:温度、海拔高度、横风、能见度等;

3)导弹参数误差:结构参数误差、气动参数误差、动力参数误差等;

4)制导控制部件误差:导航系统测量误差、导引头测量误差、舵机误差、制导控制计算机误差等;

数学教学的创新改革对社会发展的意义并不完全是传授相关知识给学生，而是要促进学生更好的掌握数学这门学科的技能以及思想方法。然而，想要改善我们目前对数学教学的方式，既可以让学生有效的学到知识，又可以提高教学效率和成果，利用数学图论竞赛是极其重要以及必要的。

2)导弹发射初始误差:速度、偏航角、横滚角、俯仰角、偏航角速度、横滚角速度、俯仰角速度误差等;

6)瞄准误差:地面照射误差、载机照射误差。

3.4　精度分析系统设计

利用Matlab/Simulink仿真工具建立精度分析系统数字仿真模型[4],如图5所示。主要包括:弹道计算模块(Trajectory Calculator_1、Trajectory Calculator_2),该模块具有所有计算参数输入功能以及标准弹道曲线和干扰弹道曲线及相关参数输出功能;导引头模块(Seeker)主要用来模拟导引头;执行机构模块(Actuator)主要用来模拟舵机系统;目标模块(Target)主要用来模拟目标运动;自动驾驶仪模块(Autopilot)主要用来实现制导控制系统模型;误差源模块(Error source)主要用来建立系统误差模型;精度分析模块(Precision analysis)主要用来进行精度分析计算并输出结果。

3.5　精度分析系统测试实例

利用精度分析系统仿真模型对某型直升机载反坦克导弹进行精度分析测试,结果如表2所示。以表2中射程6 000 m为例,精度分析系统仿真的弹道曲线如图6所示,弹着点散布如图7所示,进行精度计算结果如下:

考虑武器系统瞄准误差时,目标靶板为2.3 m×2.3 m矩形靶。

制导系统的标准偏差:δ=0.463

系统的标准偏差为:δ=0.681

圆概率误差CEP为:CEP=1.177 4×0.681=0.802

如图1所示，泳道2、5、8、11分别是4种芋螺毒腺的DNA，其条带清晰、完整和无拖尾现象；其A260/A280值在1.80～2.00，表明芋螺的基因组DNA纯度符合PCR扩增要求，且能够从200 mg毒腺中提取约9.2 μg DNA；泳道1、4、7、10分别是4种芋螺毒管的DNA，其条带部分明亮，存在降解现象，有少量的RNA片段存在；泳道3、6、9、12分别是4种芋螺的肌肉组织，其条带也是部分明亮，但蛋白含量较多。根据上述结果，毒腺基因组DNA含量最高，其次为毒管，肌肉组织最少。因此，提取芋螺毒腺基因组DNA的纯度和产率均能够符合ITS-PCR扩增的基本要求。

注重与社交网络平台的融合，注重分享，让一个人有趣的体验成为众人的饕餮盛宴，更加快速地实现旅游信息的传播，让AR成为更优秀的载体。

导弹的命中概率为:Pm=({1-exp[-2×1.152/(3.141 59×0.6812)]}{1-exp[-2×1.152/(3.141 59×0.6812)]})1/2=0.836 8

图5　精度分析系统仿真模型

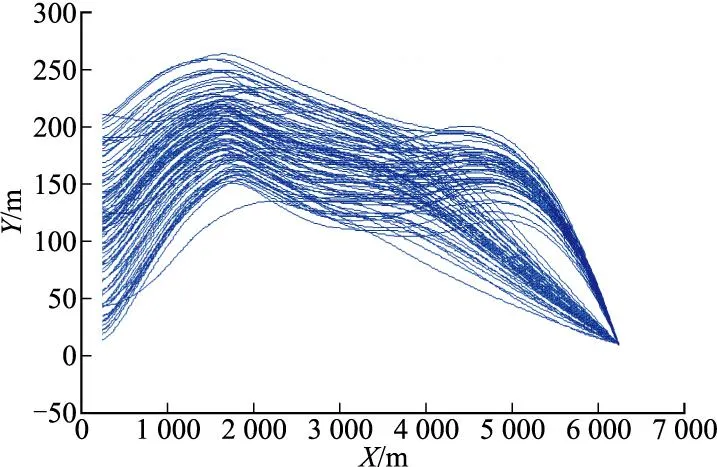
图6　弹道曲线X-Y

图7　弹着点散布图

射程/m标准偏差/m不考虑测量误差时考虑测量误差时制导测量总偏差命中概率/%CEP命中概率/%CEP40000.5210.50.72295.500.61380.100.85060000.4630.50.68198.030.54583.680.80280000.3270.50.59799.960.38590.550.703120000.4650.50.68397.960.54883.570.804

4结论

导弹控制系统采用比例导引末制导方案时,首先应满足弹道稳定性要求,当剩余飞行时间接近导引头“盲区”所对应的时间时,比例导引弹道将出现失稳现象,应对此后的比例导引信号进行处理。

将我院2016年2月—2017年2月收治的90例非小细胞肺癌患者作为研究对象，依据随机数字表法，将其分为实验组和参照组，每组患者45例，所有患者均对本次研究知情并同意；实验组男25例，女20例，年龄为42～69岁，平均年龄为（52.1±3.4）岁；参照组男22例，女23例，年龄43～68岁，平均年龄为（52.3±3.2）岁。对比两组患者性别、年龄等基础资料，差异无统计学意义（P＞0.05）。本次研究经过医院伦理委员会批准，所有患者对本研究知情并同意。

衡量制导控制系统设计结果是否满足武器系统战技指标要求,利用蒙特卡洛方法构建精度分析系统,需要对系统所有的误差源进行深入的分析和了解,得到高精度、高准确度的误差源模型后,再经过该系统大量的数字仿真试验,才能够得到置信度高的精度分析结果和制导控制系统考核结果。

参考文献:

[1]钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学 [M]. 北京: 北京理工大学出版社, 2000.

[2]彭冠一. 防空导弹武器系统控制系统设计(上): 防空导弹系列 [M]. 北京: 中国宇航出版社, 1996.

[3]袁起. 防空导弹武器系统控制系统设计(下): 防空导弹系列 [M]. 北京: 中国宇航出版社, 1996.

[4]陈佳实. 导弹制导和控制系统的分析和设计 [M]. 北京: 中国宇航出版社, 1989.

[5]刘晓侠, 杨凯, 严宪军. 反坦克导弹导引回路设计与仿真 [J]. 弹箭与制导学报, 2009, 29(6): 38-40.

[6]张意, 马清华, 陈韵, 等. 基于自抗扰控制技术的导弹控制系统设计 [J]. 弹箭与制导学报, 2012, 32(1): 37-40.

收稿日期:2014-05-12

作者简介:杨凯(1979-),男,陕西西安人,硕士研究生,研究方向:导弹制导控制系统设计与仿真。

中图分类号:TJ765

文献标志码:A

Trajectory Stability and Precision Analysis of Proportional Navigation Law

YANG Kai,ZHANG Jianling,YAN Xianjun

(No.203 Research Institute of China Ordnance Industries, Xi’an 710065, China)

Abstract:In order to analyze stability of missile in terminal guidance and its impact on accuracy, condition of trajectory stability based on proportional navigation law was studied Firstly. The design and analysis methods on trajectory stability based on proportional navigation law were proposed. Then, error source of helicopter-borne antitank missile system was modeled and the analysis system on accuracy was designed by using precision analysis methods. Finally, relying on the error source model which has high precision and accuracy and the analysis system on accuracy designed in this paper, digital simulation tests were completed and the accuracy analysis result with high confidence and the assessment result of terminal guidance control system were obtained.

Keywords:antitank missile; proportional navigation law; trajectory stability; precision analysis