基于局部搜索的Memetic差分演化算法

唐汉香++刘宇畅++唐一超

摘要：差分演化算法是一种模拟生物演化过程提出的一种基于种群的全局优化算法，但缺乏一定的局部搜索能力，从而影响的算法后期的收敛速度和解的求解精度.为了增强差分演化算法的局部搜索能力，同时平衡其勘探和开采能力，提出了一种基于局部搜索和（μ+λ）选择机制的Memetic差分演化算法算法在基本差分演化算法的基础上加入了局部搜索算法通过13个高维标准测试函数进行测试，结果表明新算法加快了算法的收敛速度，并且求解精度也优于基本差分演化算法.

关键词：差分演化算法；局部搜索算法；（μ+λ）选择；函数优化

中图分类号：TP18 文献标识码：A DOI：10.3969/j.issn.1003-6970.2015.10.004

引言

演化算法是一种基于群体的启发式搜索算法，它利用群体中的个体在解空间中进行搜索，具有白适应、自学习、白组织和隐并行性等特点.在演化过程中，群体中的个体通过遗传算子产生新个体，保持群体的多样性，对新的空间进行搜索，以得到问题的最优解.目前，演化算法已出现了很多分支，其中最主要的有遗传算法（GAs）、进化规划（EP）、演化策略（ES）和遗传程序设计（GP）、粒子群优化算法（PS0）、蚁群算法等.这些算法都有一个共同的特征，即借助生物演化的思想和原理来解决问题.

在实际工程设计中经常会涉及到一些复杂函数的优化问题，这些函数往往是非线性、不连续、不可微、多峰、多极值、非凸的，而且还带有很强的等式或不等式约束，因此，利用传统的数值算法（如：单纯性法、共轭梯度法等）很难得到理想的优化结果.近年来，许多学者把演化算法运用到复杂函数的优化中，取得了很好的效果.

差分演化算法（Differential Evolution，DE）是一种快速的演化算法，它采用实数编码，并利用个体间的差分信息来指导新产生个体的搜索.与其他演化算法相比，具有结构简单、容易使用、快速和鲁棒性等特点.近年来差分演化算法的研究受到国内外学者的广泛关注.但是，基本差分演化算法（BDE）缺乏一定的局部搜索能力，易导致收敛速度很慢.为了增强BDE的局部搜索能力，本文把传统局部搜索优化算法加入到BDE中，提出了一种高效的基于（μ+λ）选择机制的Memetic DE算法（（μ+λ）-DE）.通过13个高维标准测试函数对MDE进行了测试，结果表明新算法加快了算法的收敛速度，并且求解精度也优于基本差分演化算法

l 基本差分演化算法

函数优化问题的求解一直以来就是演化计算一个热门的研究方向，一般的，函数优化问题可以描述为：

差分演化算法是一种快速的演化算法，它采用实数编码，并利用个体间的差分信息来指导新产生个体的搜索。该算法在首届IEEE演化计算竞赛中表现突出，并获得广泛的应用，与其他演化算法相比，具有结构简单、容易使用、快速和鲁棒性等特点， 差分演化算法与其他进化算法一样大致可以分为四个步骤：初始化（Initialization）、变异（Mutation）、杂交（Crossover）和替换（Replacement）。它的主要思想是：在种群中随机选择两个不同的个体，相减得到差分向量，将此差分向量与第三个不同的个体相加得到变异个体；将这个变异个体与选择的第三个个体进行比较，如果这个个体具有更好的适应值，则替换掉第三个个体参与下一代的演化。

1.1 初始化

假设需要求解的问题有D维，种群规模为NP，则第G代种群中的第i个个体Xi，G可以表示为：

1.2 变异

差分演化算法的核心算子就是变异算子。这是它与其他演化算法最大的不同点，也是它最主要的创新点。变异操作可以使当前种群中的每一个个体或者叫目标向量xi，G产生变异向量Vi，G。下面是几种常见的变异算子：体；rl，r2，r3为种群中随机选择的与当前父个体编号i不同的5个个体的编号，即r1≠r2≠r3≠i，且r1，r2，r3∈{l，NP}；F∈[0，1+]为缩放因子，是一个实数值的约束变量，用于控制差分向量的缩放。

1.3 杂交

在完成变异操作后，进入杂交阶段，杂交算子保证了种群中的多样性。杂交操作就是种群中的目标向量xi，G。与变异阶段产生的变异向量Vi，G进行杂交产生新的试验向量Ui，G的过程。为了保证个体xi，G的进化，利用随机选择的方式使Vi，G的基因至少有一个来自于Ui，G，其他位的基因则通过杂交因子cr来确定基因的选择。杂交算子可以表示为：

其中，j=l，…，D，jrand是从范围{1，D}中随机选择的整数，用于确保尝试向量u。至少有一个基因是来自变异向量Vi，G。Cr为杂交因子，是一个（0，1）之间的值，当Cr越大，就会越多的选择变异向量Vi，G的基因，越有局部搜索和加快收敛速度；反之，Cr越小，就会越多的选择目标向量xi，G的基因，越有利于保持种群的多样性和全局搜索能力。

1.4 替换

差分演化算法的替换就是对前面经过变异和杂交产生出的孩子种群中的个体Ui，G与父亲中的个体Xi，G进行一对一的比较，具有更好适应值的个体可以存活到下一代继续进行演化。最小化优化问题的替换算子如下：

2 混合差分演化算法

2.1 Memetic DE算法

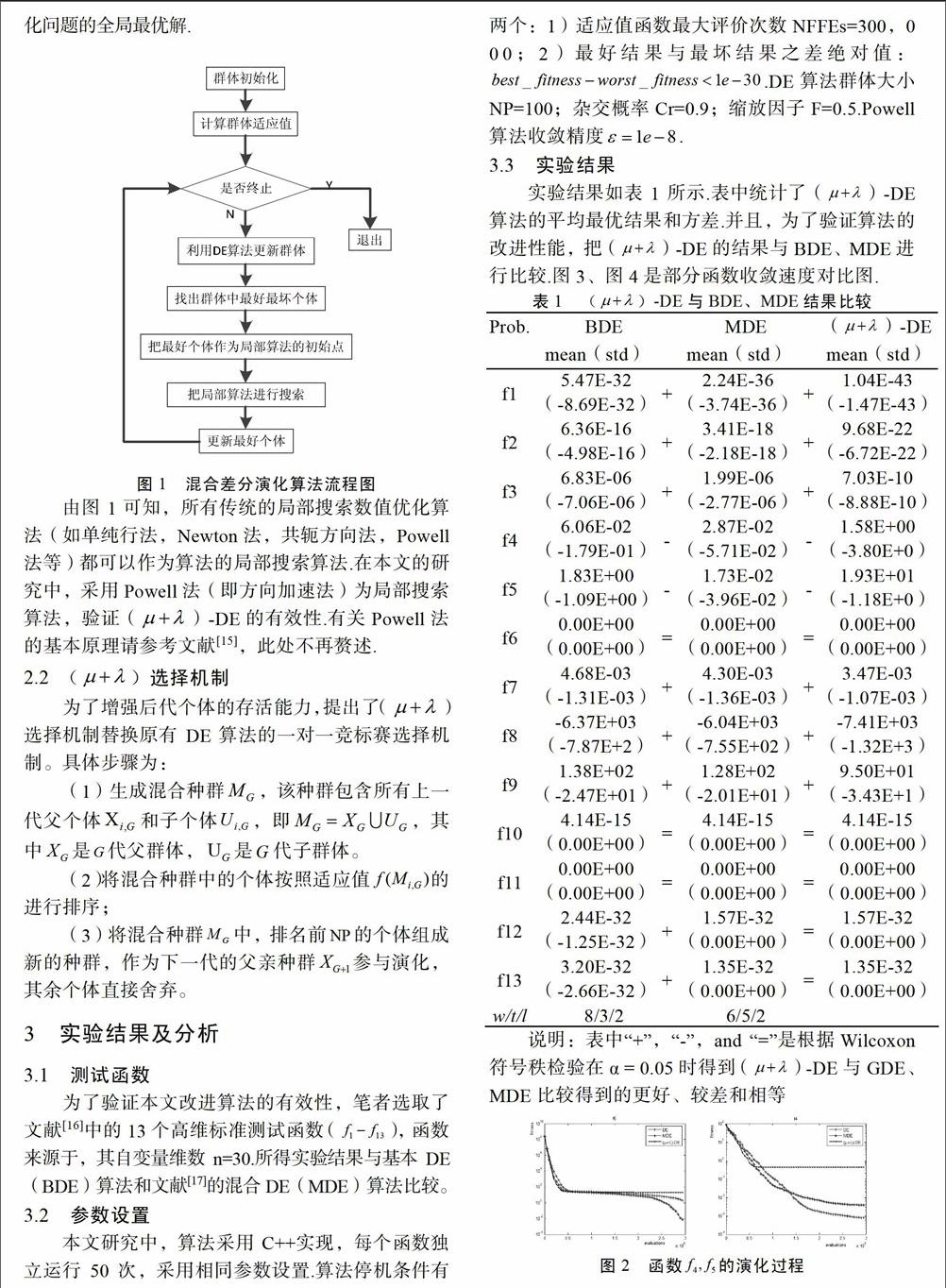
为了增强算法的局部搜索能力，加快算法的收敛速度，本文对BDE进行了改进，把局部搜索算法加入到BDE中，算法流程如图l所示：

从图l中可以看出，（μ+λ）-DE与BDE的流程大致相似.（μ+λ）-DE的主要改进之处在于：当群体利用基本差分演化算子进行更新之后，找出更新后群体的最好与最坏个体，把最好个体作为局部搜索算法的初始点进行搜索.当局部搜索达到一定精度后，所得到的新个体如果优于当前最好个体则利用新个体替换当前最好个体，使新个体作为群体中的一个个体.值得指出的是，在局部搜索算法精度合适的情况下，都能较快且稳定收敛一个局部最优解.因此，新算法一方面利用差分演化算子进行全局搜索，另一方法利用局部搜索算法在局部范围内进行搜索，从而算法可以快速地收敛于优

由图l可知，所有传统的局部搜索数值优化算法（如单纯行法，Newton法，共轭方向法，Powell法等）都可以作为算法的局部搜索算法.在本文的研究中，采用Powell法（即方向加速法）为局部搜索算法，验证（μ+λ）-DE的有效性.有关Powell法的基本原理请参考文献，此处不再赘述.

2.2 （μ+λ）选择机制

为了增强后代个体的存活能力，提出了（μ+λ）选择机制替换原有DE算法的一对一竞标赛选择机制。具体步骤为：

（1）生成混合种群MG，该种群包含所有上一代父个体Xi，G和子个体Ui，G即MG=XGUUG，其中XG是G代父群体，UG是G代子群体。

（2）将混合种群中的个体按照适应值f（Mi，G）的进行排序；

（3）将混合种群MG中，排名前NP的个体组成新的种群，作为下一代的父亲种群XG+1参与演化，其余个体直接舍弃。

3 实验结果及分析

3.1 测试函数

为了验证本文改进算法的有效性，笔者选取了文献中的13个高维标准测试函数（f1-f13），函数来源于，其白变量维数n=30.所得实验结果与基本DE（BDE）算法和文献的混合DE（MDE）算法比较。

3.2 参数设置

本文研究中，算法采用C++实现，每个函数独立运行50次，采用相同参数设置，算法停机条件有两个：1）适应值函数最大评价次数NFFEs=300，000；2）最好结果与最坏结果之差绝对值：best_fitness-worst_fitness

3.3 实验结果

实验结果如表l所示.表中统计了（μ+λ）-DE算法的平均最优结果和方差.并且，为了验证算法的改进性能，把（μ+λ）-DE的结果与BDE、MDE进行比较.图3、图4是部分函数收敛速度对比图.

说明：表中“+，，“-”，and“=”是根据Wilcoxon符号秩检验在cc=0.05时得到（μ+λ）-DE与GDE、MDE比较得到的更好、较差和相等

从表l中可以看出，在300000次最大评价次数下，（μ+λ）-DE的优化结果的平均值都比DE和MDE好或者相等。其中，函数f1-f7为高维的单峰函数，在结果没有达到最优点，从它们的最优值的平均值和标准差可以看出，（μ+λ）-DE对大部分函数的优化结果是最好的。而对于两个较差的函数f4和f5的演化过程如图2所示，从图中可以看出（μ+λ）-DE收敛效果不好的原因就是陷入了局部最优。而对于较难达到最优点的多峰问题f8-f13和很容易达到最优点，在图3中展示了最终的优化结果相差不大的函数f10，f11，f12，f13四个多峰函数的演化过程，从演化过程中可以看出，（μ+λ）-DE的收敛速度更快。从上面的分析中可以看出，（（μ+λ）-DE除了在函数f4和f5的演化过程中陷入局部最优之外，其他的优化结果都是要好于MDE和BDE的。所以，父亲和孩子种群的混合选择方式在大部分情况下是能够保持种群多样性的，并且在三种替换方式中，是能够最快收敛的。

通过上面的分析可以看出，无论是从平均最优解，还是从收敛速度上都可以看出引入了局部搜索算法的（μ+λ）-DE要优于BDE.（μ+λ）-DE利用DE算子保证了收敛于问题全局最优解的性能，同时，引入的局部搜索算法增强了DE算法的局部搜索能力，加快了算法的收敛速度.

5 结论

本文在BDE的基础上对其进行了简单的改进，把局部搜索算法加入到BDE中，提出了一种高效的基于（μ+λ）选择机制的Memetic DE算法，（μ+λ）-DE算法.（μ+λ）-DE算法由于加入了局部搜索算法，增强了DE算法的局部搜索能力，加快了算法的收敛速度.同时，由于DE算子在（μ+λ）-DE中取全局搜索的作用，所以，（μ+λ）-DE又保证了算法的全局搜索性能.

通过13个高维标准测试函数对新算法进行测试，并把结果与BDE进行比较，实验结果表明，新算法在平均最优解和收敛速度上均优于BDE算法，进而验证了改进算法的有效性.