计算极限题的若干技巧和方法

李长民

天津商务职业学院，天津300350

本文给出的这些方法有些是作者阅读高等数学书籍[1-12]获得的简明方法，有些是作者在多年的教学和科研中深入钻研的结果，其中的二重积分法解极限题则是在一般的高等数学书、数学分析、考研数学书和数学竞赛书籍上都见不到的方法，是作者在阅读一些数学大师的文集和有关极限论文[13-17]后体会到的意外收获。本文将从方程法、一重积分法、二重积分法、罗必塔法则、等价无穷小代换法、带佩亚诺余项的泰勒公式法等入手，通过重点例题和典型实例进行归纳总结。

一、方程法

利用方程法计算有些数列极限的题目，可以简化解题过程，大大降低解题的难度。

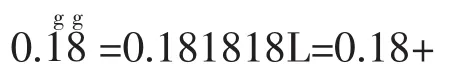
解法2：利用方程法进行创新求解。

二、用一重积分法计算极限

利用一重积分法计算极限题目是常用的求数列极限的方法，其做法是把数列的极限题目转变为一重定积分进行计算，这样能够简便、快速的得到结果。

三、用二重积分法计算极限

用二重积分法求极限的问题较少看到，其做法是把数列的极限题目转变为二重定积分进行计算，下面的例子说明用二重积分法求极限题是相当简便、有效的好方法。

四、乘“1”法

有些极限题目通过乘以等于“1”的式子，可以使较复杂的式子得以简化，然后我们可以简便的求出极限。

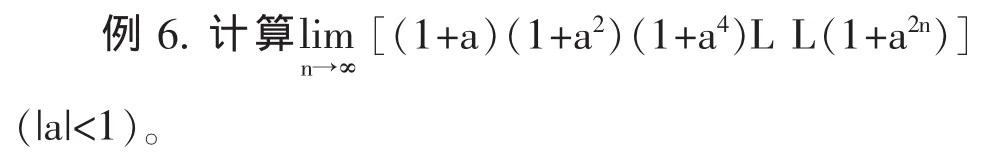
解：原式

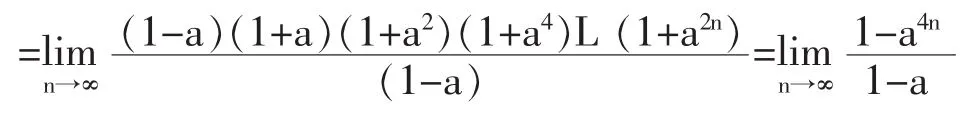
五、拆项求和法计算极限

将待求的式子通过各项的拆分相加来消除中间的大多数项，把式子简化后即可方便的求出极限。这种使用待定系数法来拆分简化和式求极限的方法，多用于数列极限题目的计算，一般的计算步骤是“先拆项求和，再取极限”。

六、利用洛比达法则求极限

应该注意，洛比达法则并不是总可以使用，如下例。

正确做法如下：

六、利用等价无穷小代换计算极限

七、利用带佩亚诺余项的泰勒公式求极限

通常我们把用高阶无穷小表示余项Rn（x）的泰勒公式称为带佩亚诺（Peano）余项的泰勒公式，其数学表达式见公式（1）。

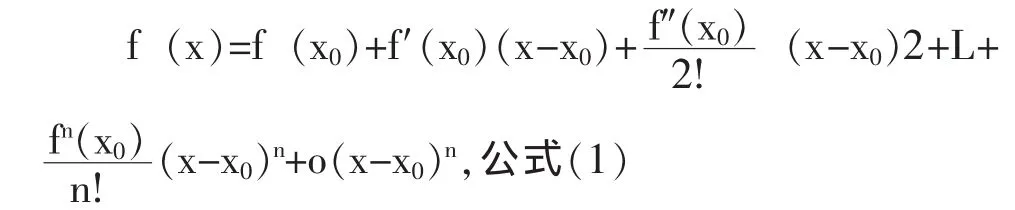
特别是，当x0=0时，泰勒公式称为麦克劳林（Maclaurin）公式，应用这种特殊形式的带佩亚诺余项的泰勒公式求当x→0时某些函数的极限，可以大大简化解题过程、降低解题难度。其数学表达式见公式（2）。

常用的带佩亚诺余项的泰勒展开式有如下6个：

分析：此式分子中含有带根号的项，用洛比达法则也可以求解，不过比较繁琐。若使用泰勒公式求解，可以将问题大大简化。

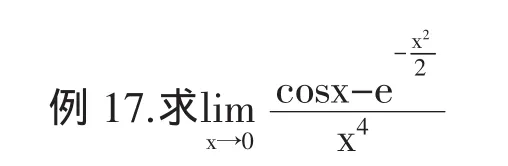
通过上面几个例子，可以看出利用带佩亚诺余项的泰勒公式求某些函数的极限具有简洁、方便、高效的效果。它不像用罗必塔法则求极限有时需要用多次，而用泰勒公式则可以一步到位，只要观察出分子、分母无穷小的阶数就可以求出结果。

八、极限问题的实际应用举例

例19.计算第二宇宙速度 （指物体脱离地球引力、在太阳系运行所具有的速度）。

解：设地球质量为M，物体质量为m，地球半径R=6.370×106米，地心为原点，将物体发射到离地面高度为h时所做的功为：

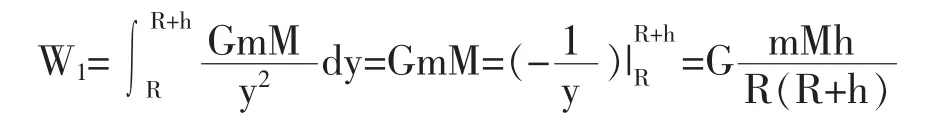
要使物体脱离地球引力场，即把物体发射到无穷远处，这相当于h→∞，因而做功总量为：

结束语：本文从多方面分析了求解极限题目的方法技巧，有些技巧和方法应用很广，在高等数学的学习中，只要我们能够灵活地运用这些解题技巧，积极思考每一种解题的方法和应用范围，认真总结解题规律，灵活巧妙地应用求极限的各种技巧，就能有效地计算极限题目。

[1]北大数学系编，数学分析[M]．北京：高等教育出版社，1986．

[2]同济大学数学教研室主编，高等数学[M]．北京：高等教育出版社，1996．

[3]陈传璋，等．数学分析（上、下册）（第三版）[M]．北京：高等教育出版社，2007．

[4]盛祥耀，等，高等数学[M]．北京：高等教育出版社，1999．

[5]龚冬宝．高等数学典型题[M]．西安：西安交通大学出版社，2000．

[6]徐兵，等．硕士研究生数学入学考试复习指导（理工类）[M]．北京：北京航空航天大学出版社，2003．

[7]滕加俊，滕兴虎．高等数学全程学习指导与习题精解（同济6版）[M]．南京：东南大学出版社，2012．

[8]李心灿．大学生数学竞赛试题解析选编（第二版）[M]．北京：高等教育出版社，2000．

[9]李大华．大学数学2000题[M]．武汉：华中科技大学出版社，2001．

[10]陈新明．用等价无穷小代换求极限中的一些问题［J］．高等数学研究，2008，（5）：5-58．

[11]钱吉林．高等数学词典[M]．武汉：华中师范大学出版社，1999．

[12]华罗庚，著，王元，校．高等数学引论（第一、二、三、四册）[M]．北京：高等教育出版社，2009．

[13]杨德庄．华罗庚文集（应用数学卷Ⅰ，Ⅱ）[M]．北京：科学出版社，2010．

[14]（美）莫里斯·克莱因．古今数学思想（第一册）[M]．上海：上海出版社，2014．

[15]吴振英，陈湛本．论极限的思想方法[J]．广州大学学报（自然科学版），2003，（5）：400-413．

[16]周述歧．数学思想和数学哲学[M]．北京：中国人民大学出版社，1993．

[17]毛骏健，顾牡．“十二五”普通高等教育本科国家级规划教材，大学物理学（上册）[M]．北京：高等教育出版社，2006．