考虑动水压力效应的高桩承台连续梁桥抗震性能评估

李　磊，张永亮，陈　敦

(兰州交通大学 土木工程学院， 甘肃 兰州 730070)

考虑动水压力效应的高桩承台连续梁桥抗震性能评估

李磊，张永亮，陈敦

(兰州交通大学 土木工程学院， 甘肃 兰州 730070)

摘要：以某深水高桩承台连续梁桥为工程背景，应用Morison方程将水对桥梁的动水压力效应按附加质量考虑，讨论了动水压力对桥梁动力特性的影响。依据2008年《公路桥梁抗震设计细则》的抗震要求，考虑动水压力效应，对该桥进行了E1、E2地震反应分析及抗震验算。分析结果表明：动水压力将明显改变高桩承台连续梁桥的动力特性；E1地震下，1#非水中墩(固定墩)和2#水中墩及桩基强度满足规范要求；考虑到损伤桩基修复困难，E2地震下对2#水中桩基的抗震性能进行了提高，经验算2#水中墩及桩基在E2地震下处于弹性状态；E2地震下，1#非水中墩(固定墩)纵桥向塑性铰区的变形能力、抗剪能力满足规范要求。

关键词：动水压力；高桩承台连续梁桥；时程分析；抗震评估

随着我国经济的快速发展及基础建设的需要，许多大型深水桥梁正在建设或者拟建当中。在地震作用下，动水压力对桥梁结构的影响不可忽视，而我国地处环太平洋地震带和亚欧地震带两大地震带之间，地震频发，烈度大[1-4]，因此深水桥梁的抗震性能受到了国内专家、学者的高度重视。

通过汶川地震桥梁结构的震害分析，发现深水梁式桥梁结构的震害主要有落梁、桥墩破坏以及支座损坏[5]。一旦深水桥梁处于水中的桥墩部分发生损坏，其修复代价将会非常巨大[5]，故应对深水桥梁的非水中桥墩和水中桥墩进行区别对待。在E1地震下，非水中桥墩、水中桥墩以及桩基础均应保持弹性工作状态；在E2地震下，非水中桥墩塑性铰区的变形能力、抗剪承载能力均应满足规范要求；水中桥墩及桩基础均应保持弹性工作状态。

由于深水桥梁结构一般都面临较深的海水和软弱的沉积岩，因此深水桥梁结构的基础均采用高桩承台基础。然而在地震作用下，高桩承台基础与水之间不可避免会发生相互作用。目前，这方面的研究工作主要有：文献[6-8]研究表明，对于深水中的桥梁结构而言，周围水的存在会对桥梁结构的动力特性和地震响应产生较大影响；文献[9]研究表明，对于深水高桩承台体系桥梁结构，承台上的动水压力采用附加质量和阻尼系数矩阵的解析解求解，单桩的附加质量采用莫里森方程求解，通过群桩系数修正得到群桩体系中各单桩的附加质量；文献[10]研究发现，非线性阻尼项对一般桥梁桩、墩结构地震反应的贡献很小，可以忽略，从而当采用Morison方程考虑水的作用时，仅计算附加惯性力。

本文以某深水高桩承台连续梁桥为工程背景，应用Morison方程将水对桥梁的动水压力效应等效为附加质量考虑，讨论了动水压力对桥梁动力特性的影响。

1工程概况

某高桩承台连续梁桥主桥为68.8 m+125 m+68.8 m变高度预应力混凝土连续梁桥，主梁断面采用C55混凝土，单箱单室结构，跨中梁高为3 m，支点处梁高为7 m，梁底采用二次抛物线渐变。桥面宽18 m，其中行车道宽14 m。桥墩采用实体式矩形桥墩(纵向尺寸及横向尺寸分别为3.5 m，9.0 m)，1#非水中墩(固定墩)墩高4.5 m，2#水中墩高6.5 m，桥墩承台尺寸为17.5 m×10.5 m×3.5 m。1#非水中墩、2#水中墩的桩基础均为钻孔灌注桩基础，桩径为2.0 m。桩基础均采用C30混凝土，2#墩采用高桩承台，从桩顶算起有9.1 m高度的桩身位于库区蓄水水位线以下。全桥总体布置图如图1所示。

图1深水高桩承台连续梁桥立面图(单位：m)

2高桩承台桥梁动水压力分析方法

采用Morison方程，计算深水桥墩、桩基础所受的动水压力作用时，动水压力一般由未受扰动的加速度场和速度场引起的沿水运动方向作用在结构上的惯性力和动水阻力组成。根据文献[10]的研究成果，本文采用Morison方程考虑动水压力作用时，仅计算附加惯性力。

2.1　承台动水压力计算方法

对于矩形承台结构，其上作用的动水附加质量采用等效圆柱体的动水附加质量乘上修正系数Kc得到[11-13]，修正系数Kc按式(1)计算。矩形截面和圆形截面等效的等效关系如图2所示。

Kc=0.94732+

(1)

(0.1≤D/B≤10)

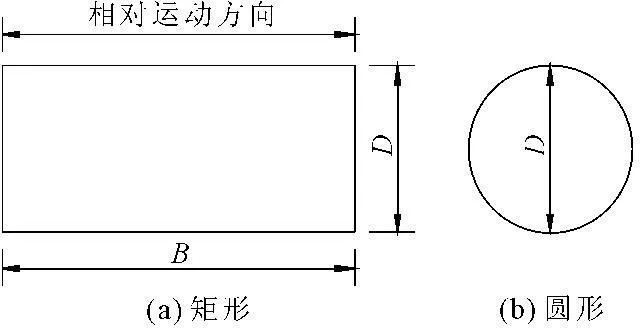
图2不同截面换算关系

2.2　桩动水压力计算方法

地震荷载作用下，基于Morison方程，单位桩长附加质量采用式(2)计算[9]：

ma=CaρΔV

(2)

式中：ma为单位桩长上的附加质量；Ca为动水附加质量系数，对于桩其值取为1；ρ为水的密度；ΔV为单位桩长的排水体积。

对于群桩基础的群桩效应，采用我国《海港水文规范》[14](JTJ213-1998)所采用的单桩上的动水压力乘以相应的群桩系数。

3动水压力对桥梁动力特性的影响

3.1　有限元计算模型

采用有限元分析软件Midas-civil建立全桥有限元模型，对其进行动力特性分析，模型中桥墩、承台及主梁均采用空间梁单元进行模拟。1#非水中墩桩土相互作用依据《公路工程抗震设计细则》[15](JTG/TB02-01-2008)的规定，简化成平动及转动弹簧施加于承台底，2#水中墩桩土相互作用简化为弹簧模拟，弹簧的刚度按m法计算。2#水中承台、桩动水压力作用按动水附加质量计算，支座按主从自由度进行模拟。全桥有限元模型如图3所示。

图3全桥有限元模型

3.2　动力特性分析

采用多重Ritz向量法，分别对高桩承台连续梁桥在考虑动水压力与不考虑动水压力两种工况下进行模态分析，得到该桥的自振频率、周期及相应的振型。在两种工况下，两者的振型特征相同，动水压力影响明显的三阶振型见图4所示。高桩承台连续梁的前5阶的自振频率及振型如表1所示。

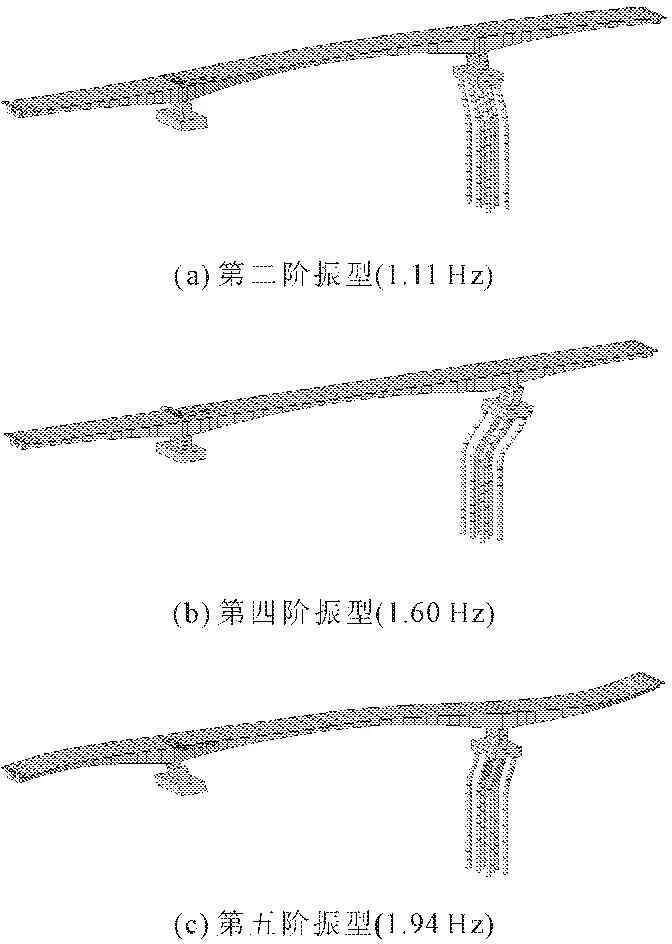
表1　高桩承台连续梁桥自振频率及振型

由高桩承台连续梁桥的自振频率及振型可知：(1) 该连续梁桥考虑动水压力效应的自振频率均比不考虑动水压力效应的自振频率小；(2) 动水压力效应对该连续梁桥的第二阶到第五阶自振频率影响比较明显，其第二阶到第四阶自振频率差值大致呈增大的趋势；(3) 该连续梁桥的第二阶至第五阶振型为2#水中墩桩基础横桥向或顺桥向弯曲振动，表明2#水中墩桩基础由于缺少土体的侧向约束作用，其顺桥向和横桥向抗弯刚度均较低，故对该桥进行地震反应分析以及抗震设计时需要重点考虑水中桩基的设计。

4E1地震下地震反应分析及抗震评估

4.1　考虑动水压力效应的反应谱分析

在E1地震作用下，1#非水中墩、2#水中墩及桩基础均应保持弹性工作状态。根据场地地震效应评价，桥址抗震设防烈度为8度，设计加速度值为0.20g，设计特征周期为0.40 s，工程场地类别为Ⅱ类，抗震设计分组为第二组，结构阻尼比取5%。对该桥按反应谱法分别计算顺桥向X和横桥向Y两个方向地震作用。地震作用与恒载作用组合后桥墩墩底及桩身内力峰值见表2所示。

表2　恒载作用与地震作用组合后结构内力表

4.2　抗震验算

桥墩配筋率为0.62%，桩基础配筋率为1.18%，计算恒载轴力下的桥墩和桩基础的屈服弯矩值，将墩底、桩身弯矩峰值与屈服弯矩进行对比。1#非水中墩墩底、2#水中墩墩底和桩基础抗震验算见表3。

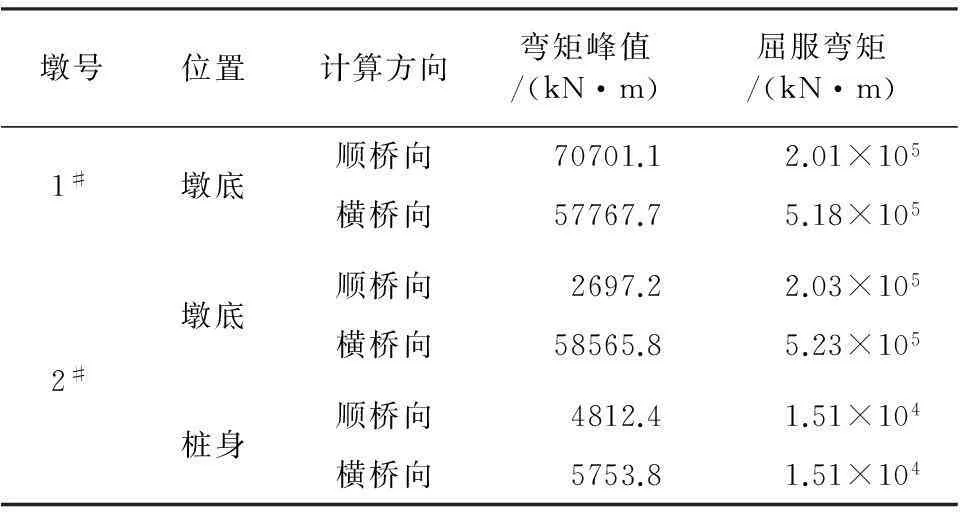
表3　1#、2#桥墩墩底以及桩基础强度验算

由表3可知：

(1) 1#非水中墩(固定墩)纵桥向的抗震性能控制桥墩的抗震设计；2#水中墩的横桥向控制桩基础的抗震设计。

(2) 1#非水中墩、2#水中墩和桩身弯矩值均小于其屈服弯矩值，该桥的抗震性能满足E1地震下的抗震设防要求。

5E2地震下地震反应分析及抗震评估

在E2地震作用下，1#非水中墩塑性变形能力和抗剪承载能力均应满足要求；2#水中墩和桩基础均应保持弹性工作状态。

5.1　1#非水中墩塑性转动能力及抗剪能力验算

5.1.11#非水中墩容许转动能力计算

为了保证E2地震下桥墩的塑性转动能力，该桥设计中，1#非水中墩的主筋采用HRB335，纵筋配筋率为0.62%，钢筋应力-应变关系采用曲线强化模型，约束混凝土应力-应变关系采用Mander模型。

采用墩底恒载轴力，用UCfyber程序计算墩底截面的弯矩-曲率关系全过程曲线。1#非水中墩墩底截面纵向的弯矩-曲率分析结果见表4，全过程曲线见图5。

表4　1#墩底截面弯矩、曲率

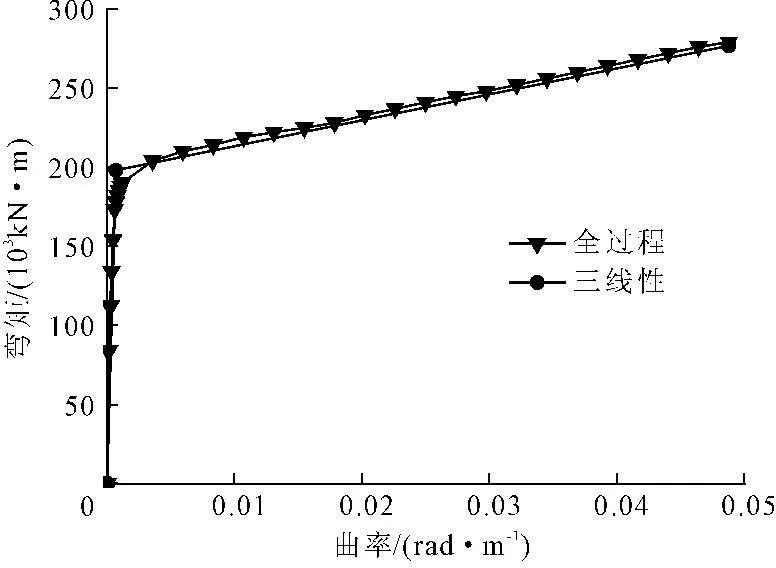
图51#墩墩底截面弯矩-曲率曲线

根据极限破坏的曲率能力按式(3)塑性铰区域的最大容许转角为：

θu=Lp(φu-φy)/K

(3)

式中：φy为截面的等效屈服曲率；φu为截面极限破坏状态曲率；K为延性安全系数，取2.0[13]；Lp为等效塑性铰长度。

等效塑性铰长度取式(4)、式(5)两者计算结果的较小值；

Lp=0.08H+0.022fyds≥0.044fyds

(4)

(5)

式中：H为桥墩高；b为桥墩的短边长度；fy为纵筋抗拉强度标准值；ds为纵筋直径。

由以上式计算得：

Lp=0.596m，θu=0.143rad。

5.1.2E2水准下1#非水中墩塑性转动能力验算

E2地震动力时程反应分析的输入地震波采用该桥桥址处的3条安全评价地震波。在1#非水中墩(固定墩)墩底沿纵桥向设置塑性铰，塑性铰的滞回规则采用Clough模型，应用Newmark-β法逐步积分求解。

E2地震作用下一条地震波作用下1#非水中墩墩底塑性铰区转角时程曲线如图6所示，墩底塑性铰弯矩—转角滞回曲线如图7所示，墩底塑性转动能力验算结果如表5所示。

图6　1#墩底塑性铰区转角时程曲线

图7　1#墩底塑性铰弯矩—转角滞回曲线

由图7和表5可知，E2地震作用下，1#非水中墩纵桥向处于屈服状态，但墩底的最大塑性铰转角小于计算容许转角值，可满足E2地震的抗震设防目标。

5.1.3E2水准下1#非水中墩抗剪能力验算

(1) 塑性铰区剪切强度验算公式

依据《公路桥梁抗震设计细则》[15](JTG/T B02-01-2008)知，抗剪强度Vcu由两部分构成，一部分为混凝土对剪切强度的贡献Vc，另一部分为箍筋的贡献Vs。计算公式如下：

Lp=0.08H+0.022fyds≥0.044fyds

(6)

(7)

式中：Ak为同一截面上箍筋的总面积,cm2；Sk为箍筋的间距,cm；fyh为箍筋抗拉强度设计值,MPa；b为沿计算方向墩的宽度,cm。

(2) 1#桥墩塑性铰区纵向抗剪验算

Vcu=4.112×104kN<5.28×104kN(由1#墩底极限弯矩反算得到)，说明1#桥墩塑性铰区纵向抗剪强度不满足规范要求。当配箍率μ增大到0.69%时，Vcu=5.430×104kN>5.28×104kN，1#桥墩塑性铰区纵向抗剪强度满足规范要求。

5.2　2#水中墩承载能力及桩基础抗震验算

如果水中桥墩及桩基础在地震中发生损伤，其加固维修的费用非常昂贵，因此,对2#水中墩及桩基础采用弹性设计方法进行抗震设计。在E2地震作用下，2#水中墩及桩基础始终处于弹性状态。

根据E2地震下的弹塑性时程反应分析得2#水中墩墩底弯矩峰值、桩基础的最大弯矩值。当桩基础纵筋配筋率达到2.5%、配箍率达到3.0%时，桩基础最大弯矩值小于其屈服弯矩值，故2#水中墩桩基础处于弹性状态。2#水中墩以及桩基础抗震验算见表6所示。

表6　2#墩及桩身强度验算　单位：kN·m

6结论

通过考虑动水压力效应，对该高桩承台连续梁桥进行了E1、E2地震下的地震反应分析及抗震性能验算。结果表明：

(1) 动水压力将明显改变高桩承台连续梁桥的动力特性；

(2) E1地震下，1#非水中墩(固定墩)和2#水中墩及桩基础的强度满足规范要求；

(3) 考虑到水中桥墩震后损伤修复困难，E2地震下对2#水中桩基础的抗震性能进行了提高，经验算2#水中墩及桩基础在E2地震下处于弹性状态；

(4) E2地震下，1#非水中墩(固定墩)纵桥向塑性铰区的变形能力、抗剪能力满足规范要求。

参考文献：

[1]王克海.桥梁抗震研究[M].北京：中国铁道出版社,2007.

[2]戴晓春,袁明.高速铁路长联大跨连续梁桥地震响应分析[J].桥梁建设,2006(S2):144-146.

[3]禚一,王菲.罕遇地震下城际铁路连续梁桥延性抗震设计[J].铁道工程学报,2012(4):66-72.

[4]邓小伟.基于两水平设防的连续梁桥抗震性能分析[J].石家庄铁道大学学报：自然科学版,2012,25(4):39-42.

[5]庄卫林,刘振宇,蒋劲松.汶川大地震公路桥梁震害分析及对策[J].岩石力学与工程学报,2009,28(7):1377-1387.

[6]赖伟,王君杰,韦晓,等.桥墩地震动水效应的水下振动台试验研究[J].地震工程与工程振动,2006.26(6):164-171.

[7]朱日希，高学奎.桥梁抗震分析中动水压力的计算[J].中国铁道科学，2007，28(3):44-48.

[8]赖伟,王君杰,胡世德.桩基础承台水平附加质量分析[J].同济大学学报：自然科学版,2004，32(10)：1339-1343.

[9]曹新建,熊永光,傅翼,等.地震作用下桥梁结构-水相互作用分析[J].结构工程师，2010，26(4):69-73.

[10]袁迎春,赖伟,王君杰,等.Morison方程中动水阻力项对桥梁桩柱地震反应的影响[J].世界地震工程，2005，21(4):88-94.

[11]冀伟,刘世忠.动水力作用时矩形空心墩刚构桥地震响应分析[J].世界地震工程,2010,26(2):2-6.

[12]王君杰,赖伟,胡世德.深水高桩基础桥梁地震动水效应分析[J].同济大学学报：自然科学版,2011,39(5):650-655.

[13]宋波,李悦.高桩承台动水力简便计算方法[J].北京科技大学学报,2011,33(4):509-514.

[14]中华人民共和国交通部.JTJ213-1998海港水文规范[S].北京：人民交通出版社，1998.

[15]中华人民共和国交通部.JTG/TB02-01-2008公路桥梁抗震设计细[S].北京：人民交通出版社，2008.

DOI:10.3969/j.issn.1672-1144.2015.04.006

收稿日期：2015-03-13修稿日期：2015-04-21

基金项目：国家自然科学基金资助项目(51468031)

作者简介：李磊(1989—)，男，甘肃兰州人，硕士研究生，研究方向为桥梁结构抗震。E-mail:956889743@qq.com

中图分类号：U442.5+5 文献标识码： A 文章编号： 1672—1144(2015)04—0028—05

Seismic Performance Evaluation of Continuous Girder Bridges with Elevated Pile Caps Considering the Effect of Dynamic Water Pressure

LI Lei, ZHANG Yongliang, CHEN Dun

(SchoolofCivilEngineering,LanzhouJiaotongUniversity,Lanzhou,Gansu730070,China)

Abstract：Taking a continuous girder bridge with deep elevated pile caps as the engineering background, the dynamic water pressure on bridge foundation was considered as additional quality according to Morison equation, and the influence of dynamic water pressure on the dynamic characteristics of the bridge was discussed. Under E1 and E2 earthquake, the seismic response analysis and aseismic calculation were carried out based on the requirements of seismic resistance in the Guidelines for Seismic design of Highway Bridges(2008 Edition) with the consideration of dynamic water pressure. The analysis results indicate that: dynamic water pressure will significantly change the dynamic characteristics of the continuous girder bridge with elevated pile caps; under E1 earthquake, the strength of 1#pier (fixed pier) out of water and 2#pier as well as piles foundation in water can meet the requirements of the guidelines; under E2 earthquake, considering difficult repair of the damaged piles, the seismic performance of 2#piles foundation in water are improved, which are in the elastic state during the earthquake; under E2 earthquake, the longitudinal plastic hinge deformation capacity and shear capacity of 1#pier out of water (fixed pier) can meet the requirements of the guidelines.

Keywords:dynamic water pressure; continuous girder bridge with elevated pile caps; time history analysis; aseismic evaluation