基于不同横断面形式的桥梁墩台受力性能数值分析

唐先习，周勇超，尹月酉

(1.兰州理工大学 土木工程学院， 甘肃 兰州 730050； 2.长安大学 公路学院， 陕西 西安 710064)

基于不同横断面形式的桥梁墩台受力性能数值分析

唐先习1，周勇超2，尹月酉1

(1.兰州理工大学 土木工程学院， 甘肃 兰州 730050； 2.长安大学 公路学院， 陕西 西安 710064)

摘要：为研究水平荷载作用下不同横断面形式的桥梁墩台的受力性能，建立了横断面面积相同、形状不同的桥梁墩台的有限元模型，并进行相应的应力和位移数值分析。结果表明，在相同截面面积和外荷载作用下，不同横断面形式的墩台底部第一主应力与墩台顶部最大位移均呈规律性变化。在此基础上，文章对不同截面形式墩台的受力性能的优劣性进行了分析。研究结果对于桥梁墩台结构构造的确定，具有一定的参考价值。

关键词：桥梁工程；墩台横断面形式；数值分析；受力性能

桥梁墩台在桥梁结构中起着“承上启下”的作用。桥梁墩台不但要承受上部结构产生竖向力、水平力和弯矩，还要承受风力、土压力、流水压力以及可能发生的地震力、冰压力、船只和漂流物对墩台的撞击力等的作用，因此，对桥梁墩台在不同荷载作用下受力性能的研究至关重要。

在关于桥梁墩台受力性能的研究方面，较多的偏重于桥梁墩台的强度、刚度及稳定性分析等方面的研究[1-6]，而关于墩台构造方面的研究则相对较少，特别是关于桥梁墩台横断面形式的研究则更少。在这一方面，孙治国等[7]通过试验，验证了钢筋混凝土墩柱等效塑性铰长度与墩柱高度、截面宽度、纵筋直径等的关系。彭亚军等[8]对预制吊装结构常用的四种墩形通过计算分析，研究了墩壁厚、横隔板道数、隔板厚度对局部稳定的影响程度。张扬[9]则对墩身纵、横向刚度，墩顶弹性水平位移以及高墩的稳定性进行详细论述，介绍不同墩身截面形式的构造特点和适用范围。以上对于桥梁墩台形式的研究，并未对不同截面形式的墩台在水平荷载作用下的局部应力进行较详细的分析，但这些局部应力对于墩台的受力性能特别是耐久性能起着非常重要的作用，因此，本文主要从这方面展开研究。

1分析目的及模型

1.1　数值分析目的

本文主要采用ANSYS模型，对不同横断面形式的桥梁墩台进行模拟。通过对墩台身在桥梁结构纵向水平荷载作用下的受力性能进行分析，研究不同横断面的墩台应力分布规律及位移变化规律，以确定不同情况下桥梁墩台适宜的横断面结构构造。对于钢筋混凝土桥墩，当水平荷载值在一定范围内时，桥墩的水平位移随受到的荷载近似呈线弹性变化。因此，本文在进行数值分析时采用线性分析的方法。

1.2　桥梁墩台有限元分析横截面选取

在进行数值分析时，墩台的有限元模型采用底部固结、顶部自由的方式。墩台横断面采用等截面，面积取1 m2，墩台高度取10 m。施加荷载为沿桥梁结构纵向的水平荷载，施加荷载的位置选在墩台顶部，荷载取10 kN。进行应力分析时，选取墩台底部应力最大的截面进行；进行位移分析时，取墩台顶部位移最大截面进行。桥墩断面的形状分别采用正方形、带圆角的正方形、圆形、长方形、带圆端的长方形以及带尖端的长方形，进行相应的数值分析。

2数值模拟结果及分析

2.1　不同边长比的矩形截面受力性能数值分析

不同边长比的矩形截面，墩台的截面尺寸采用表1中所列的值，施加荷载的方向垂直于截面的长边。

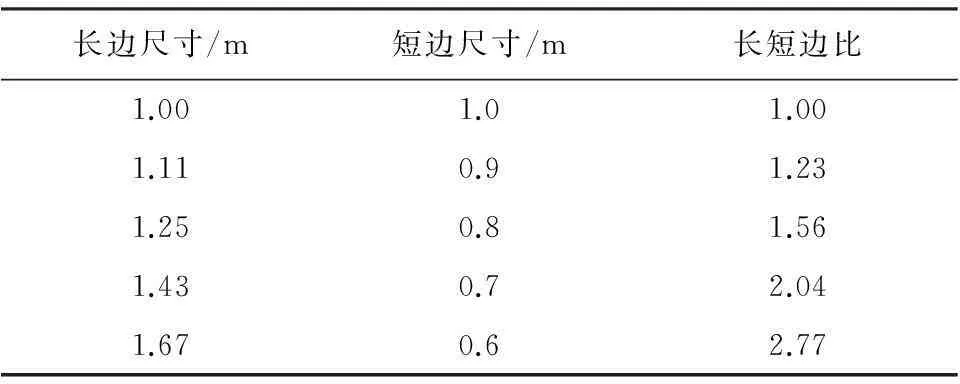
表1　矩形墩台截面尺寸表

水平荷载作用下墩台底部第一主应力分布云图见图1， 不同长短边比例的墩台底部受拉侧面第一主应力值最大，取其有代表性的分布曲线进行分析，见图2～图4，不同边长比时墩台底部不同部位应力曲线见图5，不同边长比时墩台顶部水平位移曲线见图6。

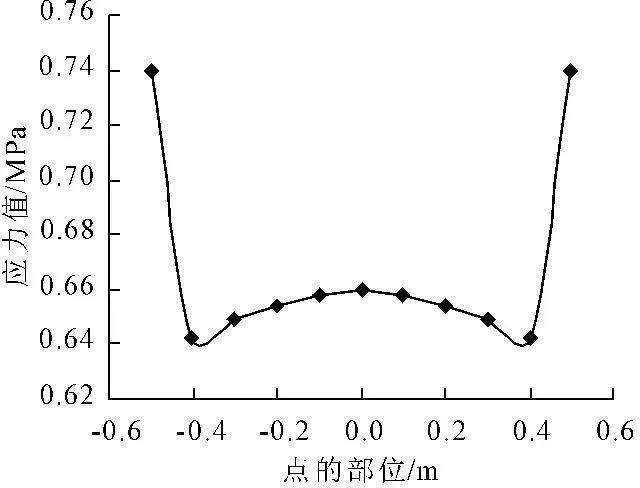
图1　墩台底部第一主应力分布云图

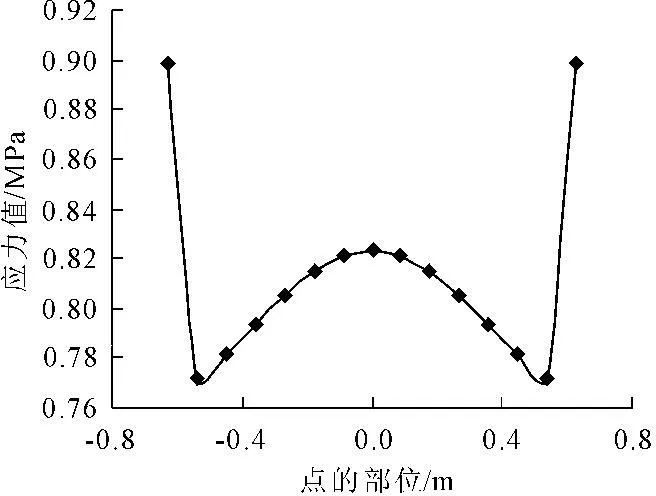
图2　边长比为1∶1时受拉侧面第一主应力分布曲线

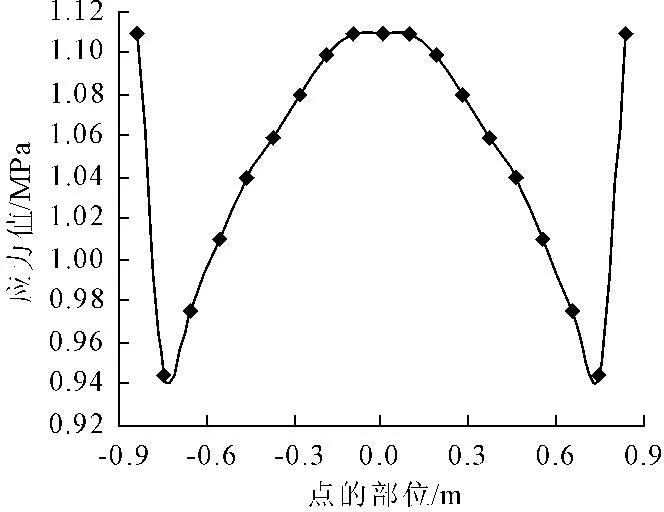
图3　边长比为1.56∶1时受拉侧面应力分布曲线

图4边长比为2.77∶1时受拉侧面应力分布曲线

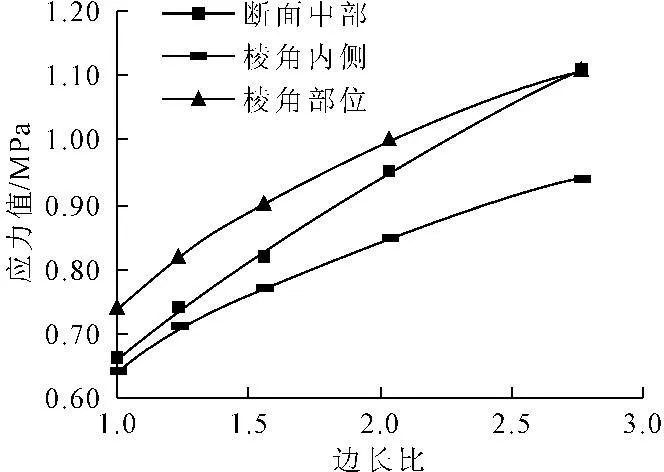
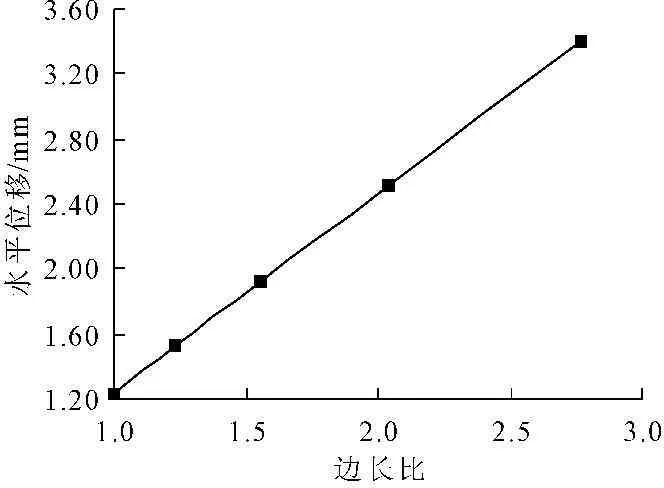
图5　不同边长比时受拉侧面各部位应力曲线

图6不同边长比时墩顶水平位移曲线

图1为墩台底部第一主应力分布云图。由图1可以看出，对于矩形截面墩而言，当在桥墩顶部沿垂直于墩台的长边方向施加水平荷载作用时，墩台横断面上的第一主应力顺着施加荷载的方向逐渐变小，由拉力逐渐变为压力。

图2～图4为不同边长比时具有代表性的墩台底部受拉侧面第一主应力分布曲线，图中点的位置为零处即为长边的中部。由图2～图4可以看出，当在桥墩顶部沿垂直于墩台的长边方向施加水平荷载作用时，受拉侧面底部断面所受最大主应力沿断面呈现一定的变化规律，即在断面中部主应力较大，向两边逐渐变小，到断面边缘时主应力则突然增大。

图5为矩形墩在不同边长比时各部位应力变化曲线，结合图2～图4，选取的部位包括断面中部、应力最小的棱角内侧和发生应力突变的棱角部位。由图5可以看出，当矩形墩的横断面面积一定时，随着矩形截面长短边比例逐渐增大，断面中部、棱角内侧、棱角部位的第一主应力值均不断增大，其中断面中部的应力值增大幅度最大，但各应力的增加幅度随长短边比值的增大而不断减小。因此，进行墩台设计时，在满足工程要求的前提下，应尽量减小矩形的长短边比值。

由图5还可以看出，当矩形的边长比值小于2.77时，断面中部应力值小于棱角部位应力值，当矩形的边长比超过2.77时，断面中部的应力值已超过棱角部位的应力值。因此，进行钢筋的布置时，应考虑这方面的因素。

图6为矩形墩在不同边长比时墩顶水平位移曲线。由图6可看出，对矩形墩而言，当墩的横断面面积不变时，施加相同的荷载，墩顶位移随墩的长短边比值的增大而增大，两者之间近似呈线性关系。此关系对于桥梁墩台截面的设计，具有非常重要的意义。

2.2　正方形、带圆角正方形、圆形截面受力性能数值分析

以上仅对矩形截面的桥墩应力分布进行了分析，下面对相同横截面积的正方形、带圆角的正方形以及圆形截面受相同荷载时的应力分布进行分析。不同截面形式的矩形墩数值分析结果见图7～图14。

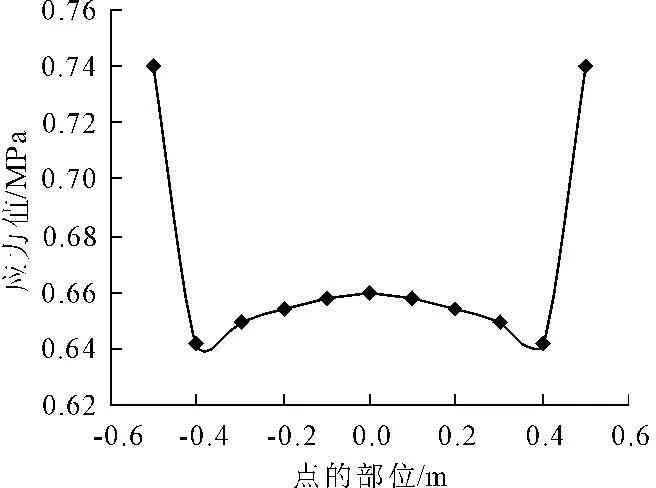
图7　正方形墩台底部第一主应力分布云图

图8　正方形墩台底部受拉侧面第一主应力分布曲线

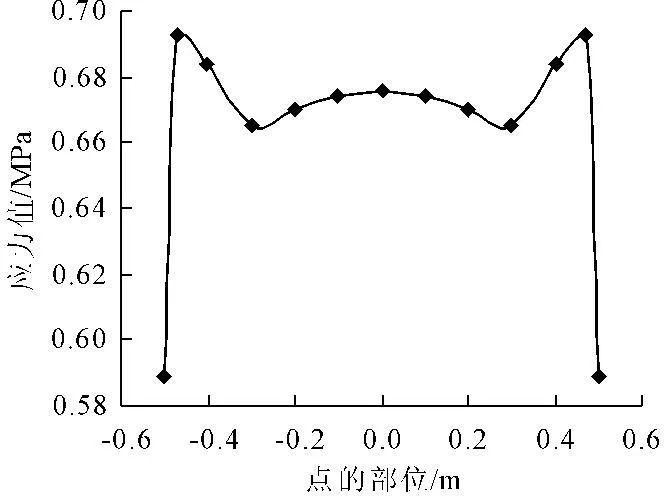
图9　带圆角正方形墩台底部第一主应力分布云图

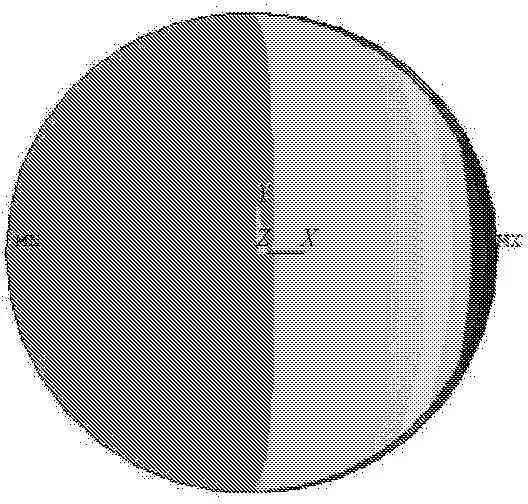
图10　带圆角正方形墩台底部受拉侧面第一主应力分布曲线

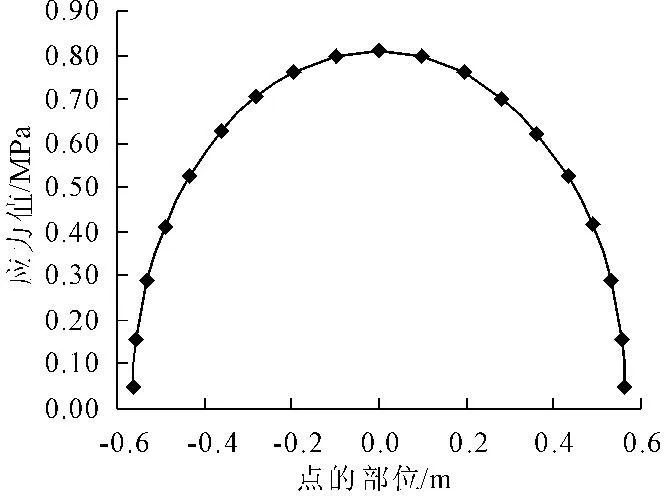
图11　圆形墩台底部第一主应力分布云图

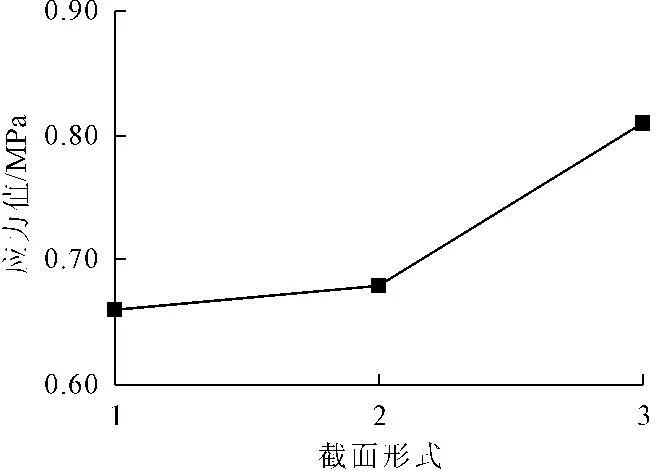
图12　圆形墩台底部受拉侧面第一主应力分布曲线

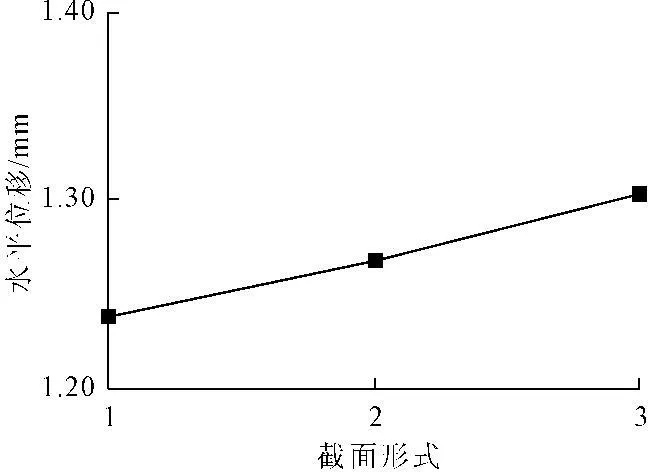
图13　不同截面形式受拉侧面中部最大应力曲线

图14不同截面形式的墩顶水平位移曲线

图7～图12分别为具有相同横断面面积的正方形桥墩、具有圆角的正方型桥墩以及圆形桥墩的第一主应力分布规律。从以上的分布规律可以看出，正方形断面的棱角处会出现较大的应力突变。而对于具有圆角的正方形截面，由于圆角的出现，应力变化值相对较小，整个受拉侧面上应力值的变化相对较小。最后出现的曲线端部应力下降较多，主要是此时取值点已与截面中部不在一个平面上，而向中和轴靠近的原因。对于圆形截面而言，由于整个受拉侧面为圆顺的曲线，而未出现明显的转折角，因此未发生应力突变的现象。

图13为不同截面形式的受拉侧面中部最大应力值曲线，图14为不同截面形式的墩顶水平位移变化曲线，其中1代表正方形截面，2代表带圆角的正方形截面，3代表圆形截面。从图13可以看出，从正方形、带圆角正方形到圆形截面，第一主应力的值逐渐增大。从图14可以看出，从正方形、带圆角正方形到圆形截面，墩顶水平位移值逐渐增大。

2.3　长方形、带圆端长方形、带尖端长方形截面受力性能数值分析

以上分析中，未涉及到矩形、带圆端的矩形以及带尖端的矩形的应力分布规律，下面则对这几方面进行分析。在进行数值分析时，各横断面的面积均为1 m2，宽度均取0.6 m，带尖端的矩形尖端为直角。施加荷载方向垂直于截面的长边。不同截面形式的桥墩台数值分析结果见图15～图22。

图15　长方形墩台底部第一主应力分布云图

图16长方形墩台底部受拉侧面第一主应力分布曲线

图17　带圆端长方形墩台底部第一主应力分布云图

图18　带圆端长方形墩台底部受拉侧面

图19　带尖端长方形墩台底部第一主应力分布云图

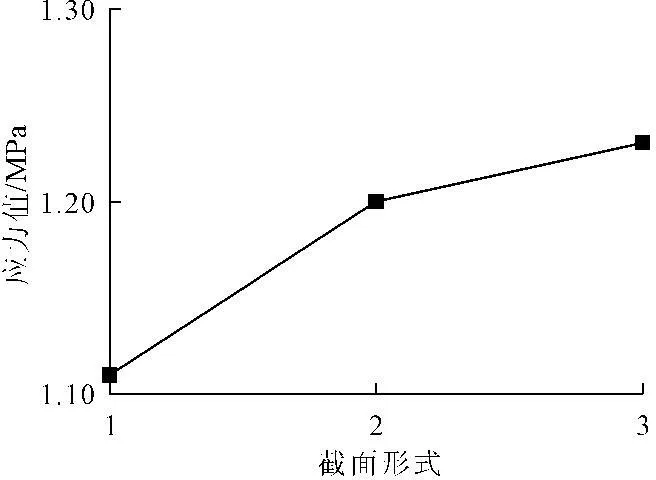
图20　带尖端长方形墩台底部受拉侧面

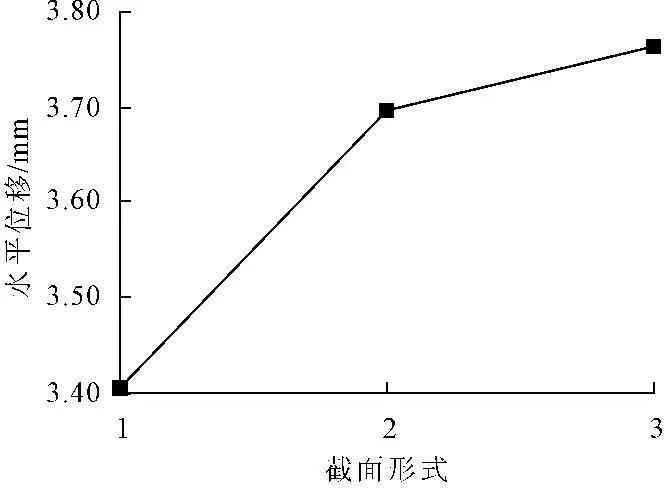
图21　不同截面形式的墩底受拉侧面

图22不同截面形式的墩顶水平位移曲线

图15～图20分别为具有相同横断面面积和相同宽度的长方形桥墩、带圆端的长方形桥墩以及带尖端的长方形桥墩的第一主应力分布规律。通过对这三种截面形式桥墩的第一最大主应力的分布规律可以看出，在具有圆端形的墩面上，应力突变的趋势几乎不再发生。通过与带圆角的正方形应力分布图进行对比可知，圆半径的增大，可在一定程度上减小应力突变的出现，这同时也与模型建立时单元的划分有一定的关系。

通过对圆端形和尖端形墩的应力分布规律的对比可知，在尖端形墩转角处，仍然存在着较明显的应力突变现象。通过分析可知，转角处的转角越大，应力突变也越大。

图21为不同截面形式的墩底受拉侧面中部最大应力值曲线，图22为不同截面形式的墩顶水平位移变化曲线，其中1代表长方形截面，2代表带圆端的长方形截面，3代表带尖端的长方形截面。从图21可以看出，从长方形、带圆端长方形到带尖端长方形截面，第一主应力的值逐渐增大。从图22可以看出，从长方形、带圆端长方形到带尖端长方形截面，墩顶水平位移值逐渐增大。

3结论

(1) 对矩形截面桥墩而言，随着矩形截面长短边长的比值逐渐增大，受拉侧断面中部、棱角内侧、棱角部位的第一主应力值均不断增大，其中断面中部的应力值增大幅度最大。而墩顶水平位移随墩的长短边比值的增大而增大，两者之间近似呈线性关系。

(2) 从正方形截面、带圆角正方形截面到圆形截面，第一主应力的值逐渐增大，墩顶水平位移值也逐渐增大。因此，为避免正方形截面墩的棱角部位的应力突变，应将棱角部位设为圆角。

(3) 从长方形、带圆端长方形到带尖端长方形截面，第一主应力的值逐渐增大，墩顶水平位移值逐渐增大，但增大的值较小。同时圆端形矩形截面比尖端形矩形截面在消除应力突变方面具有较大的优势。

(4) 文章虽然从静力方面对混凝土桥梁柱式墩台的受力性能进行了分析，但在对结构进行动力性能研究时，往往取其在某极限状态时的受力情况按静力形式进行分析，因此研究结果对桥梁墩台的动力性能分析也具有一定的参考价值。

参考文献：

[1]刘鸣，陆本燕，刘伯权.钢筋混凝土桥墩破坏模式识别方法[J].中国公路学报，2011，24(3):58-63,79.

[2]何铭华,辛克贵,郭佳.新型自复位桥梁墩柱节点的局部稳定性研究[J].工程力学,2012,29(4):122-127.

[3]戴公连,闫斌,魏标.门式墩纵向刚度及其对无缝线路纵向力的影响[J].华中科技大学学报，2012，40(11):33-36.

[4]LIU Haitao. The mechanical property of high bridge pier[J]. Advanced Materials Research, 2013,639-640:678-681.

[5]郑罡，李贵乾.钢筋混凝土桥墩有效刚度[J].土木工程学报，2013,46(6):44-52.

[6]刘岳兵,王少华,黄梅,等.盆式橡胶支座结构及混凝土墩台非线性有限元分析[J].铁道建筑,2010(9):28-30.

[7]孙治国，王东升，郭迅，等.钢筋混凝土墩柱等效塑性铰长度研究[J].中国公路学报，2011,24(5):56-64.

[8]彭亚军，马玉全，许佳波.预制吊装结构桥墩受力性能研究[J].黑龙江交通科技,2013(7):88-89.

[9]张扬.连续钢构桥高墩设计关键技术及选型研究[J].铁道标准设计，2014，58(9):85-88.

DOI:10.3969/j.issn.1672-1144.2015.04.003

收稿日期：2015-01-31修稿日期：2015-03-10

基金项目：国家自然科学基金项目(51168030)

作者简介：唐先习(1972—)，男，山东济宁人，博士， 副教授，主要从事大跨度桥梁施工与桥梁耐久性的研究。E-mail: 695913483@qq.com

中图分类号：U443.2

文献标识码：A

文章编号：1672—1144(2015)04—0012—06

Numerical Analysis of the Mechanical Performance of Bridge Piers with Different Cross-section Forms

TANG Xianxi1, ZHOU Yongchao2, YIN Yueyou1

(1.SchoolofCivilEngineering,LanzhouUniversityofTechnology,Lanzhou,Gansu730050,China;2.SchoolofHighways,Chang'anUniversity,Xi'an,Shaanxi710064,China)

Abstract：For the study of the mechanical performance of bridge piers with different cross-section forms under the action of horizontal load, the finite element models of bridge pier with same area but different shapes of cross-section were established, and the corresponding numerical analysis of stress and displacement was carried out. The results showed that, under the same load some performances of the bridge piers with same area but different cross-sections changed regularly. The performances were the principal stress of the pier bottom and the maximum displacement of the pier top. On this basis, the advantages and disadvantages of piers with different cross-section forms were analyzed in the article. The results have a certain referential value to the determination of bridge pier structures.

Keywords:bridge engineering; pier cross-section form; numerical analysis; mechanical performance