基于不同岩石破坏方式的滚刀效率评价模型研究

赵贺兴，王述红，昝世明，梅　林

(东北大学 资源与土木工程学院， 辽宁 沈阳 110819)

基于不同岩石破坏方式的滚刀效率评价模型研究

赵贺兴，王述红，昝世明，梅林

(东北大学 资源与土木工程学院， 辽宁 沈阳 110819)

摘要：目前对TBM滚刀破岩效率评价大多采用量化计算破岩比能(ηse)的方法，其中岩石破碎体积为影响破岩比能的关键因素，岩石在滚刀作用下的破坏体积与其破坏方式关系密切。为此，结合岩石不同破坏方式，讨论了岩石破碎体积的一种简易实用的计算方法。基于岩石破坏过程中以剪切破坏和张拉破坏为主的特性，提出了以岩石破坏时裂纹长度与剪切面在岩石自由表面投影长度以及滚刀刀刃宽度之间的关系来识别岩石破坏方式，在此基础上计算岩石破碎体积，结合CSM预测模型，推导出一种破岩比能水平量化计算方法。通过实例对该方法进行计算验证，分析了破岩比能(ηse)与刀间距(S)、刀具磨损量(w)之间的关系，得出了ηse-S曲线与ηse-w曲线，表明存在最优刀间距，且随着磨损量增大，比能值也将增大。所述的预测模型能够对TBM破岩时刀间距的优化、刀具的更换提供理论依据。

关键词：破岩比能；CSM模型；岩石破碎体积；刀间距；刀具磨损量

目前在硬质岩土中修建隧道，进行机械自动掘进施工时多采用全断面岩石隧道掘进机[1](Tunnel Boring Machine，TBM)。在软岩中应用TBM仍需做出相应的应对措施[2]。TBM在硬岩中掘进主要依靠滚刀滚压岩石，滚刀破岩效率直接关系到TBM的破岩能力和掘进成本，对TBM性能具有决定性影响[3]。

滚刀作用下的岩石破碎方式，目前并未有一个满意的共识。美国科罗拉多矿业学院提出了剪切破岩理论[4]；东北工学院(即现东北大学)岩石破碎实验室[5]提出拉伸破坏观点，认为其属于裂纹扩展拉伸破坏。随着研究的深入，有学者提出刀具破岩为一个复杂作用的过程，如张照煌[6]提出其为剪切破坏为主，而以挤压和张拉破坏为辅；蒋吉吉[7]提出当围压较低时，岩石呈现以张拉破坏为主的拉剪综合失效模式，围压的增长使得岩石破坏模式逐渐过渡为以剪切破坏为主的拉剪综合失效模式。本文在结合前人研究的基础上，讨论了CSM预测模型下的比能计算方法及其影响因素，提出在TBM滚刀作用下岩石以剪切破坏和张拉破坏为主，并以岩石破坏时裂纹长度与剪切面在岩石自由表面投影长度以及滚刀刀刃宽度之间的关系来识别岩石的破坏方式，从而计算岩石破碎体积，推导出一种破岩比能简易计算方法，通过工程实例计算验证了该方法的有效性，并分析了破岩比能与刀间距、刀具磨损量之间的关系，为TBM刀间距的优化、刀具的更换提供参考。

1CSM模型下的破岩效率评价方法

在盘型滚刀工作过程中，刀具所受作用力Ft的各向分力分别为垂向力、滚动力和侧向力[8]。由于侧向力Fs较小[9]，因此通常可不考虑侧向力影响。滚刀受力示意图如图1所示[10]。

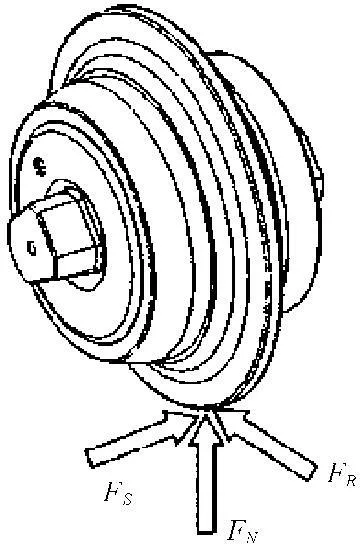
图1滚刀所受各向分力示意图

本文采用刀具破岩比能值作为破岩效率评价参数。比能(Specific Energy，SE)是研究刀具破岩效率的重要指标，采用能量法，将其定义为刀具滚压破坏单位体积岩石所消耗的能量[11]。其值表示为：

(1)

式中：ηse为比能；FN为滚刀所受垂直力；FR为滚刀所受滚动力；p为滚刀贯入度；l为滚刀滚动切削行程；V为岩石破碎体积。∑FN认为是刀盘所受总垂向力;∑FR·l认为是刀盘所受总扭矩。

对于盘形滚刀所受作用力Ft，本文采取应用最为广泛的由科罗拉多矿业学院(ColoradoSchoolofMines，CSM)提出的CSM预测模型[12-13]进行估算。此模型在数学分析的基础上经大量试验验证，已经在众多工程中得到了成功应用，比其他模型具有更高准确性[14-15]。该模型不考虑滚刀所受侧向力，其示意图如图2所示。

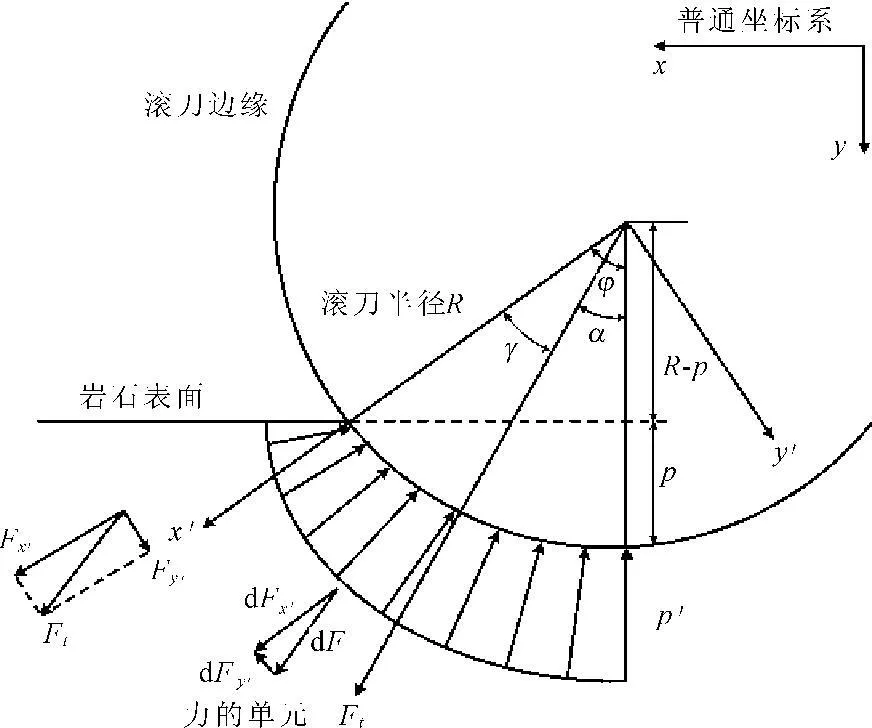
图2基于CSM模型的滚刀作用下岩石压力分布

盘形滚刀所受作用力Ft值为：

(2)

(3)

(4)

(5)

式中：Ft为滚刀所受到的作用力合力；φ为滚刀刀刃与岩石的接触角度；γ为接触区内一点与刀刃初始接触岩石表面点间的夹角，其值为0～φ；α为Ft与岩石表面法线间的夹角，其值可认为是0.5φ；p为滚刀贯入度；T为滚刀刀刃宽度；R为滚刀半径；p′为破碎区任意一点的压力；P0为滚刀正下方破碎区基本压力，与滚刀布置和工作条件(滚刀间距S和贯入度p)、滚刀尺寸(滚刀半径R和滚刀刀刃宽度T)、岩石强度(岩石抗压强度σc和抗拉强度σt)有关；ψ为刀尖压力分布系数，其值为-0.2～0.2，当滚刀刀尖宽度较大时取ψ=-0.2，当滚刀为V形且锋利时取ψ=0.2，一般情况下取ψ=0.1；C为无量纲系数，常取值为2.12。

联立式(2)～式(5)，则可以由下式(6)和式(7)计算出滚刀所受的垂向力FN和滚动力FR：

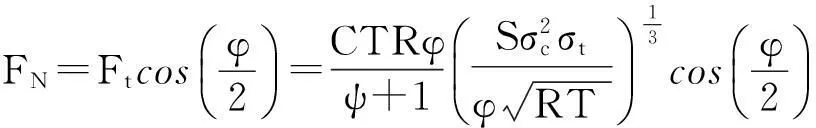
(6)

(7)

将式(6)和式(7)代入到式(1)中，即可求出刀具破岩比能值。根据式(1)，对于比能值的计算，岩石破碎体积V是一个十分重要的影响参数。本次讨论主要推导了不同条件下的岩石破坏体积的计算公式，从而更加有效地计算刀具破岩比能值。

2岩石破碎体积计算方法

2.1　岩石破坏方式分析

TBM滚刀作用于岩石上，其目的是使表面岩石碎块掉落，而非将岩块碾磨成岩屑[16]。岩石破碎体积与其破坏方式联系紧密，结合文献[4-7,10]的分析，对其破坏方式进行简化考虑，认为岩石受滚刀作用形成的受压粉核区较小，滚刀破岩过程主要以岩石剪切破坏和张拉破坏为主，并通过分析岩石破坏时裂纹长度和剪切面在岩石自由表面投影长度以及滚刀刀刃宽度之间的关系来判断具体破坏方式。

根据文献[10,17]，岩石在刀具作用下形成压碎破坏区之后产生的侧向裂纹扩展长度L经数值模拟方法拟合得到的计算公式为：

(8)

(9)

Kic=0.145σt

(10)

式中：L为侧向裂纹扩展长度；FN为单刀法向推力；d为滚刀刃型尺寸；μ为泊松比；E为弹性模量；Kic为断裂韧性；Gic为临界能释放率。

2.2　不同破坏方式下岩石破碎体积计算

本文认为TBM上每把刀的受力情况与破碎岩石情况均相同，则岩石破碎体积可按下式(11)计算：

V=∑l·S′

(11)

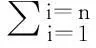
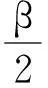
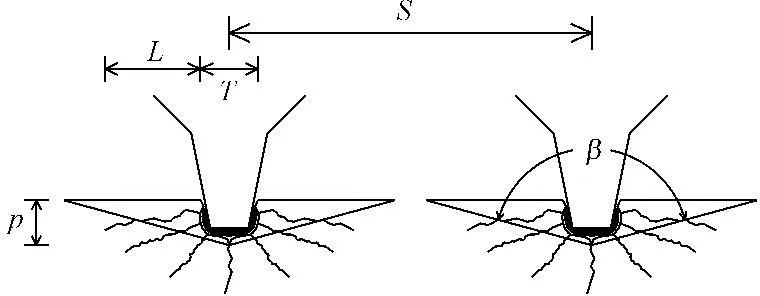
图3岩石破碎截面(情况1)

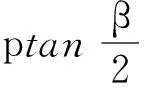
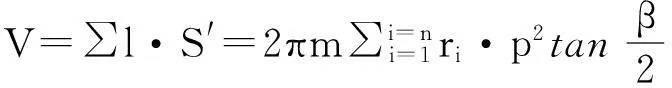
(12)

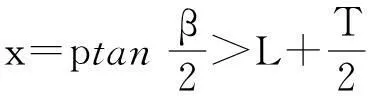
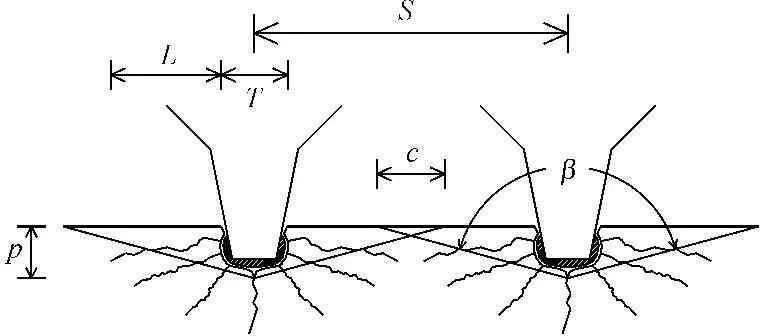
图4岩石破碎截面(情况2)

(13)

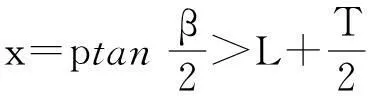
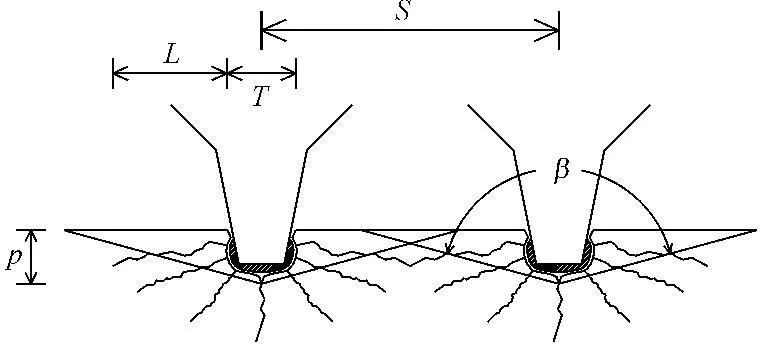
图5岩石破碎截面(情况3)

此时滚刀间剪切面有所交叉，且同时侧向裂纹发生交汇贯通。引入控制参数破坏厚度系数λ，当裂纹向岩石深部扩展交汇贯通时λ>1，当裂纹平行于岩石自由表面扩展交汇贯通时λ=1，当裂纹向岩石自由表面扩展交汇贯通时取λ<1。图5所示情况下，认为滚刀之间属协同破坏岩石，岩石属于剪切-张拉破坏，以剪切破坏为主，岩石截面破碎面积S′=λSp，岩石破碎体积：

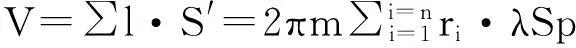
(14)

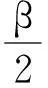
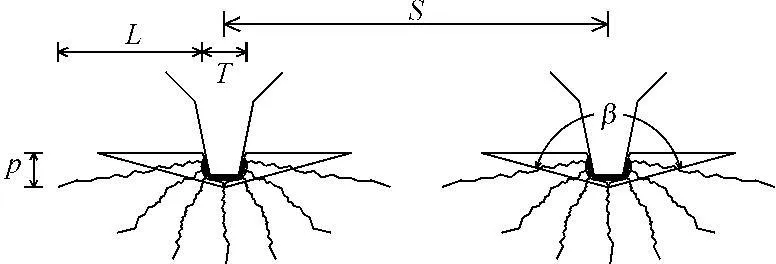
图6岩石破碎截面(情况4)

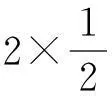
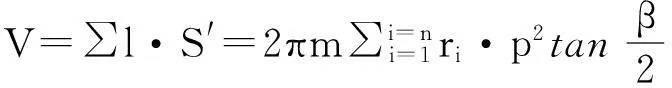
(15)

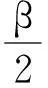
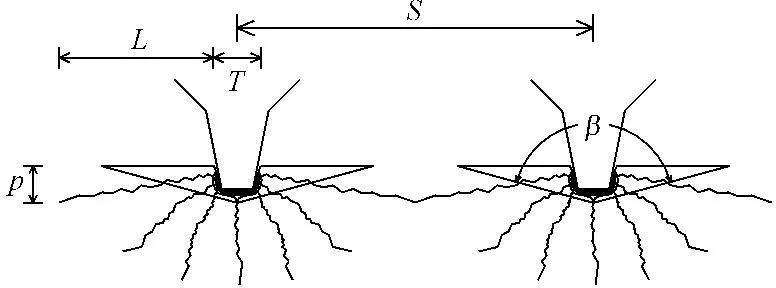
图7岩石破碎截面(情况5)

此时刀刃间侧向扩展裂纹发生交汇贯通，从而使滚刀之间的岩石剥落破坏。仍引入前述控制参数破坏厚度系数λ，则图7所示情况下，可认为滚刀之间属于协同破坏岩石，岩石属于剪切-张拉破坏，且以裂纹张拉扩展破坏为主，岩石截面破碎面积S′=λSp，岩石破碎体积：

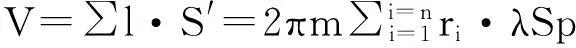
(16)

3工程实例

以秦岭隧道实际工程[19]为例，采用本文提出的计算方法，分别计算了该工程所使用的TBM在刀盘旋转一周时所受的总垂向力，总扭矩和总岩石破碎体积。秦岭隧道的岩石以混合花岗岩和混合片麻岩为主，抗压强度平均在150 MPa左右，抗拉强度6 MPa左右。该工程采用的TBM刀盘刀具平面布置示意图如图8所示，刀盘刀具布置侧向示意图如图9所示。

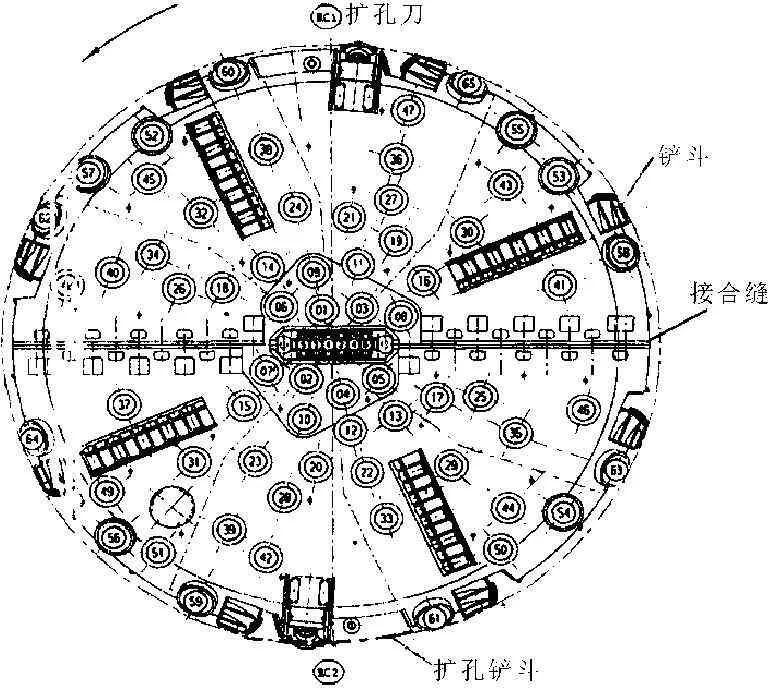
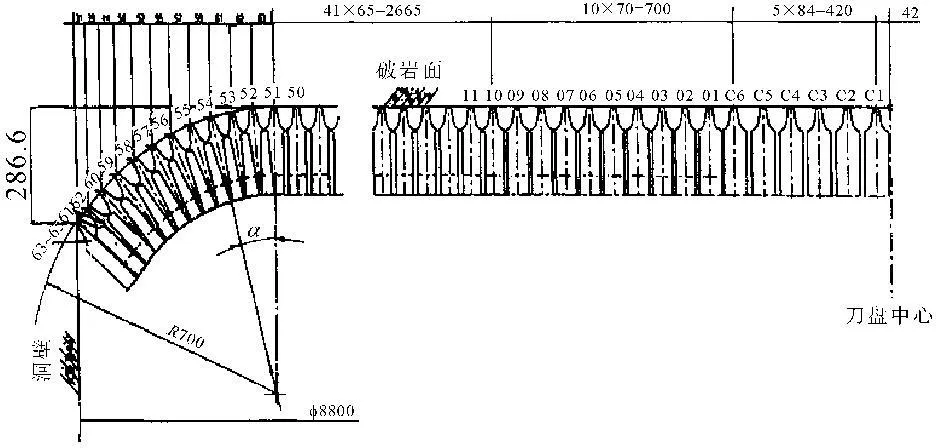
图8　刀盘刀具平面布置示意图[19]

图9刀盘刀具侧向布置示意图[19]

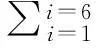
本文根据实际地质条件和掘进机刀具布置，计算参数取值如下[19]：

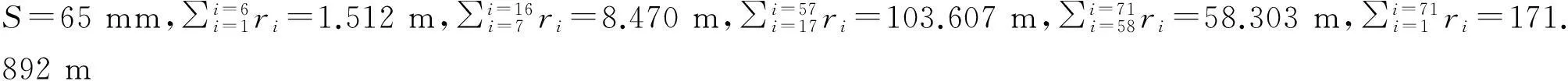
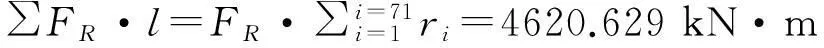
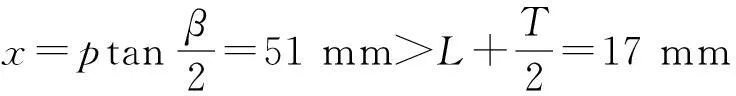
由文献[19]分析本文计算结果如表1所示。

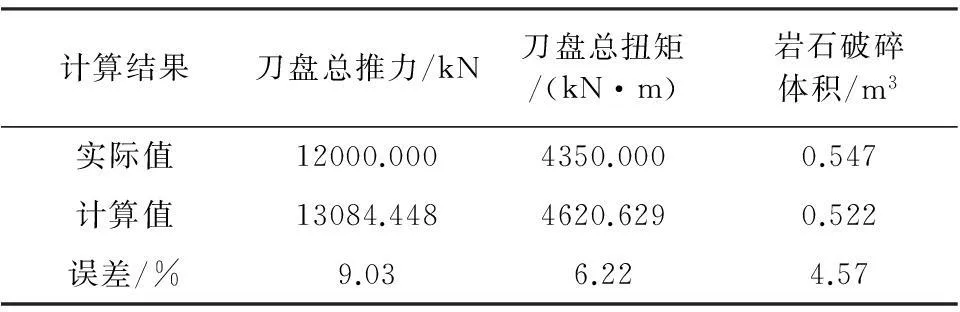
表1　实际值与计算值对比

可见，误差值均处于10%以下的水平，且计算所得岩石破碎体积较为准确。由此数据结合式(1)，即可得到TBM滚刀刀具破岩比能值。说明本文提出的模型能较好的对TBM施工过程进行预测分析。

4比能与工程参数关系分析

通过以上方法得出某工程的比能值之后，即可依此值进行TBM滚刀破岩效率分析。由比能计算公式(1)可见，当某工程采用的TBM刀具及地质条件确定后，即可通过该式选取最合理刀间距，以此降低TBM滚刀破岩比能，提高掘进效率。也可结合比能值，通过监测滚刀刀具实时半径R′，根据滚刀出厂半径R，计算磨损量w=R-R′，由于磨损量会对滚刀破岩比能产生影响，因此及时更换刀具将能够保证掘进效率。

本文参考秦岭隧道工程参数，绘制了比能-刀间距曲线(ηse-S曲线)与比能-磨损量曲线(ηse-w曲线)，如图10、图11以及图12所示。

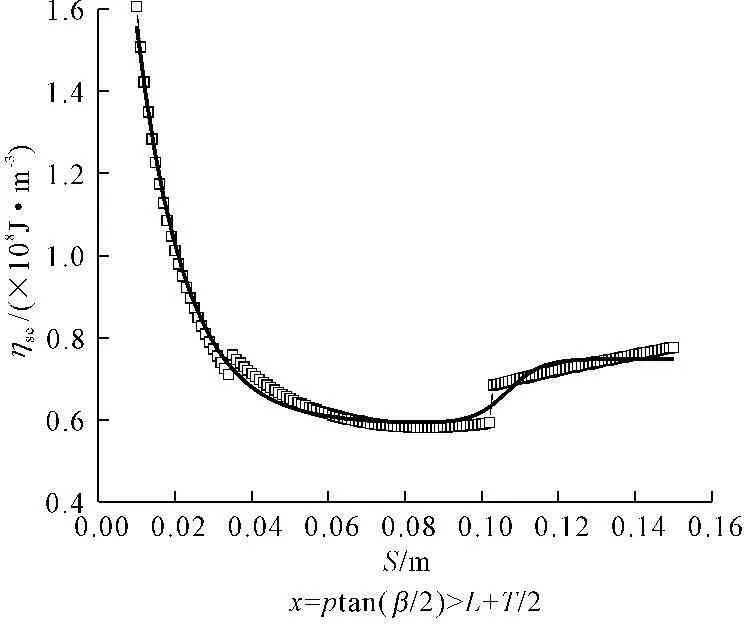
图10比能-刀间距曲线(情况1)

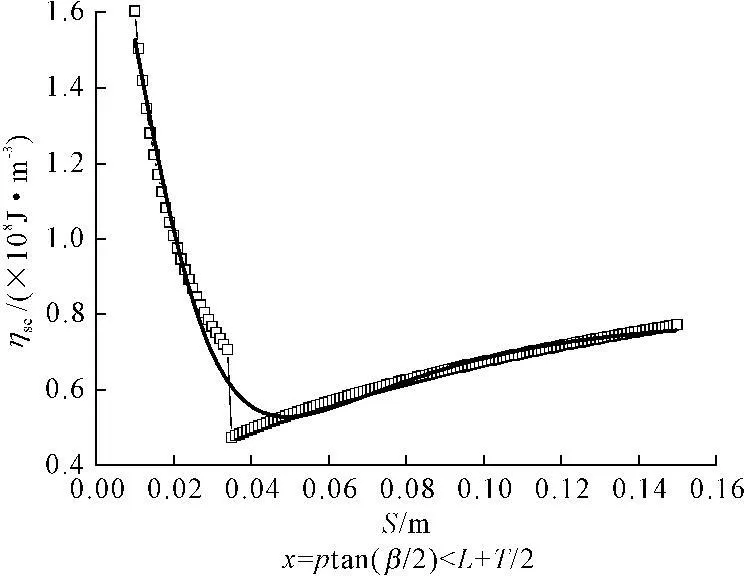
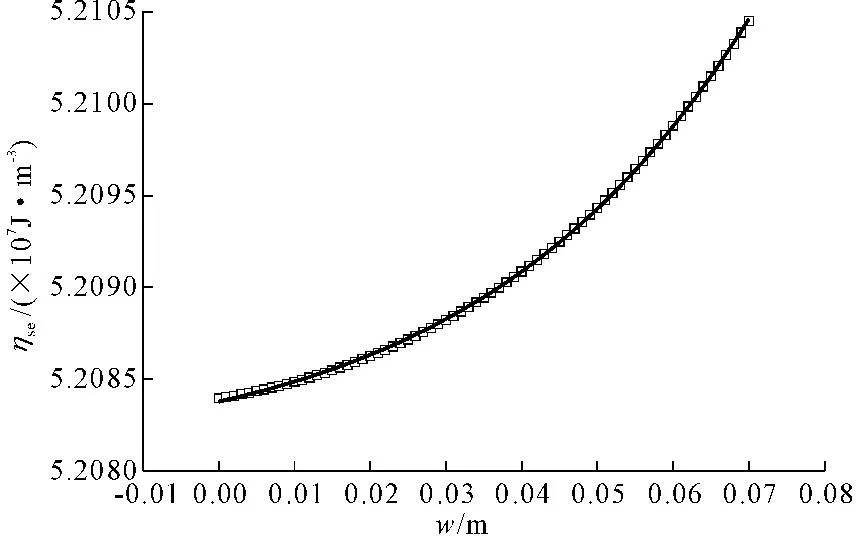
图12比能-磨损量曲线

由图10与图11可见不论岩石破坏方式如何，均存在一个能使破岩比能最小的刀间距值，当刀盘设计时采取该值，将能极大提高TBM滚刀破岩效率。由图12可知，随着滚刀磨损量变大，滚刀破岩比能值也将变大，对提高滚刀破岩效率不利，因此是否及时更换刀具将直接关系到TBM施工时滚刀作用下岩石破碎的效率。

5结论

本文针对TBM刀具破岩时岩石以剪切破坏和张拉破坏为主，提出一种简易方法计算岩石破碎体积，结合CSM预测模型，从而得出破岩比能值，分析了滚刀刀间距与滚刀磨损量对破岩比能的影响，得出了如下结论：

(1) 以岩石破坏时裂纹长度与剪切面在岩石自由表面投影长度以及滚刀刀刃宽度之间的关系来识别岩石破坏方式的方法可行，在此基础上计算岩石破碎体积从而得出破岩比能水平的方法有效，可依据此模型分析滚刀所受作用力与每把滚刀作用下岩石破碎体积；

(2) 破岩比能值反映了破岩效率的大小，破岩比能值越小，滚刀破岩效率越高；

(3) 得出ηse-S与ηse-w曲线，所提预测模型可对TBM的刀间距优化、刀具更换提供理论参考依据。破岩比能与许多因素相关，其中存在最优刀间距，在刀盘设计时应允以考虑；刀具磨损量将影响滚刀破岩效率，应注意在施工过程中合理更换刀具。

参考文献：

[1]Lu Y, Ma J M, Xu Q J, et al. TBM in the Future of China[J]. Marine Georesources and Geotechnology，2004，22(3)：185-193.

[2]高燕芳.TBM掘进技术在软岩隧洞中的应用[J].水利与建筑工程学报，2011，9(6)：126-128.

[3]Rostami J, Ozdemir L, Nilson B. Comparison between CSM and NTH hard rock TBM performance prediction models[C]//Proceedings of Annual Technical Meeting of the Institute of Shaft Drilling Technology. Las Vegas，1996.

[4]Ozdemir L, Wang F D. Mechanical tunnel boring prediction and machine design[R]. Colorado School of Mines, 1979.

[5]金国栋，黄士芳，虞和霁，等.全断面岩石隧道掘进机盘刀破岩机理分析[J].制冷空调与电力机械，1981(3)：1-9.

[6]张照煌.全断面岩石掘进机盘形滚刀破岩机理的探讨[J].矿山机械，1995(10)：27-29.

[7]蒋吉吉.TBM盘形滚刀破岩机理的试验与模拟研究[D].长沙：中南大学，2014.

[8]Yagiz S. A model for the prediction of tunnel boring machine performance[C]//Proceedings of the International Association for Engineering Geology and the Environment. Nottingham，2006.

[9]Gertsch R E. Rock toughness and disc cutting[D]. Missouri：University of Missouri-Rolla，2000.

[10]朱逸.TBM多滚刀组合破岩特性的数值模拟及实验研究[D].长沙：中南大学，2013.

[11]Acaroglu O, Ozdemir L, Asbury B. A fuzzy logic model to predict specific energy requirement for TBM performance prediction[J]. Tunnelling and Underground Space Technology，2008，23(5)：600-608.

[12]Rostami J, Ozdemir L. A new model for performance prediction of hard rock TBMs[C]//Proceedings of the Rapid Excavation and Tunneling Conference，Metallogy & Exploration，INC，1993.

[13]Ozdemir L. Development of theoretical equations for predicting tunnel boreability[D]. Golden：Colorado School of Mines，1977.

[14]Gertsch R, Gertsch L, Rostami J. Disc cutting tests in colorado red granite: implications for TBM performance prediction[J]. International Journal of Rock Mechanics and Mining Sciences，2007，44(2)：238-246.

[15]Gong Q, Zhao J. Development of a rock mass characteristics model for TBM penetration rate prediction[J]. International Journal of Rock Mechanics and Mining Sciences，2009，46(1)：8-18.

[16]Cho J W, Jeon S, Yu S H, et al. Optimum spacing of TBM disc cutters: A numerical simulation using the three-dimensional dynamic fracturing method[J]. Tunnelling and Underground Space Technology，2010，25(3)：230-244.

[17]Liu H Y, Kou S Q, Lindqvist P A. Numerical studies on Bit-Rock fragmentation mechanisms[J]. International Journal of Geomechanics，2008，8(1)：45-67.

[18]郭牡丹，朱浮声，王述红，等.岩体非贯通结构面的岩桥贯通准则研究[J].岩土工程学报，2013，35(8)：1513-1518.

[19]张厚美.TBM的掘进性能数值仿真研究[J].隧道建设，2007，26(S2)：1-7.

DOI:10.3969/j.issn.1672-1144.2015.04.002

收稿日期：2015-03-06修稿日期：2015-04-11

基金项目：国家自然科学基金(51474050；51179031；51074042)；国家自然科学基金外国青年学者研究基金(51250110531；51350110534)；地质灾害防治与地质环境保护国家重点实验室(SKLGP2012K009；SKLGP2014K011)；辽宁省高等学校优秀人才支持计划(LN2014006)

作者简介：赵贺兴(1990—)，男(满族)，河北唐山人，硕士研究生，研究方向为TBM滚刀破岩。E-mail:zhhxing1@163.com

中图分类号：U455.3

文献标识码：A

文章编号：1672—1144(2015)04—0006—06

Model Study on the Efficiency Evaluation of TBM Disc Cutters Based on Different Kinds of Rock Fragmentation Methods

ZHAO Hexing, WANG Shuhong, ZAN Shiming, MEI Lin

(CollegeofResources&CivilEngineering,NortheasternUniversity,Shenyang,Liaoning110819,China)

Abstract：To evaluate the efficiency of TBM disc cutters, the common practice is to calculate the specific energy for rock breaking with the volume of fragmentized rocks as the key influencing indicator. Different fragmentation methods result in varied volumes of fragmentized rocks when adopting TBM disc cutters. Based on the study of different fragmentation mechanism, such as shear failure, tensile failure, compression failure and the combination of multiple failure modes, a simple method to calculate the volume of fragmentized rocks was put forwarded. Based on the fact that the shear failure and tensile failure are the main forces during the fragmentation, an identification method of different failure modes was suggested based on the quantitative relationship of the crack length, the projected length of the shear failure surface and the width of the cutter. And then the volume of fragmentized rocks was calculated to derive a new algorithm that could quantify the specific energy with the help of a CSM model. Finally, an example was used to prove the feasibility of this method. The relationship between specific energy and the cutter space, also the relationship between specific energy and the wear condition was analyzed, from which the ηse-S curve and the ηse-w curve were obtained. This application proves that there is an optimal cutter space, and the ηseincreases with the wear condition. This model could be used to provide a reference for the performance prediction and optimization of TBM disc cutters.

Keywords:specific energy; CSM model; the volume of fragmentized rocks; cutter space; wear condition