动力机器基础的数值模拟与Lysmer解析法之比较

朱　飞，彭红明，雷有德，曹程明

(1.青海省环境地质勘查局青海省环境地质重点实验室， 青海 西宁 810007；2.甘肃中建市政工程勘察设计研究院， 甘肃 兰州 730000)

动力机器基础的数值模拟与Lysmer解析法之比较

朱飞1，彭红明1，雷有德1，曹程明2

(1.青海省环境地质勘查局青海省环境地质重点实验室， 青海 西宁 810007；2.甘肃中建市政工程勘察设计研究院， 甘肃 兰州 730000)

摘要：把基础和地基作为整个弹性共同体系，应用数值分析方法，分别对不同地基深度、不同荷载分布以及不同基础尺寸等条件下的模型进行仿真分析计算，并把结果与相应的Lysmer方程所得的计算结果进行对比分析，确定了准确的数值分析所应满足的具体的建模条件并验证了Lysmer方程的正确性。

关键词：动力机器基础；弹性半空间；数值方法

对动力机器基础的设计所依据的理论和方法中，最主要的有质-阻-弹模式、弹性半空间模式[1-5]以及数值模拟方法[6]。其中，由赖斯纳提出的弹性半空间模式，尽管其在数学、力学上是严密的，而且对方程中的主要参数，如地基刚度和阻尼，能够给出很好的物理解释，但是其计算复杂，不易于一般工程技术人员掌握。赖斯默(J. Lysmer)应用 “比拟法”，将复杂的半空间问题转化为简单的等效质-弹-阻模型来计算，得到了对半空间理论实用化的Lysmer方程式，使弹性半空间理论便于工程界掌握和应用。但是对于Lysmer方程的正确性和精确性等方面的研究工作，却很少有学者进行过有效的验证。近几十年来得到广泛应用的数值模拟方法，采用有限单元法，将实际的无限自由度体系代之以有限自由度的离散化模型，对复杂的基础振动问题进行求解，依靠现代电子计算机强大的分析计算能力，使求解过程更加便携性，结果更加准确性[7-8]。针对上述问题，本文应用数值模拟方法，建立合理的有限元模型，在地基模型深度、荷载分布形式、基础模型尺寸等方面进行数值仿真分析探讨，进而对Lysmer方程进行数值验证。

1分析模型

土体半空间表面在竖向集中谐和力作用下的解答是基础震动半空间理论的一个基本理论课题[1]。由于此问题是一个轴对称问题，用图1所示描述比较方便。

图1土体半无限空间在荷载作用下的动力响应模型

首先建立协和振动下轴对称问题的波动方程，确定边界条件后，再通过汉克尔变换，结合波动方程和边界条件，可得出

(1)

以上就是基础表面竖向位移的积分形式解，或称拉姆问题的积分形式解。

在竖向谐和力σz=σ0eiωt作用下的竖向振动问题，由赖斯默解出。它所依据的标本是原质变参等效集总的竖向振动方程

(2)

经过变化可得出：

(3)

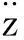
2动力机器基础的有限元计算方法

2.1　计算的思路和目的

本文研究的主要目的在于应用数值分析方法验证Lysmer方程以及探索数值分析方法对于动力机器基础设计的准确性等方面所应满足的一些具体的模拟条件。本文研究的主要思路是通过模拟不同荷载分布形式、不同基础横截面尺寸、不同模型深度等条件下的计算结果与理论结果进行对比，最后得出对动力机器基础进行数值仿真分析时，在何种具体的条件下能够得出与理论结果相比较精确的解答，最后验证Lysmer方程的正确性。

2.2　有限元的计算建模方法(边界尺寸、力学参数、荷载形式)

首先建立几何模型，根据弹性半空间理论，应建立圆柱形模型，但因为实际计算时的困难性等方面原因，本文建立立方柱体模型。为便于计算，利用其对称性，建立1/4模型进行计算；根据具体实验数据，确定基础和地基各自分别的密度、弹性模量以及泊松比等力学参数；在基础表面施加均布正弦周期力作用，模型四周和底面施加相应的边界条件。

3模型计算结果分析

3.1　计算模型

建立立方柱形地基及基础模型，见图2。基础模型尺寸：横截面为2.4 m×2.4 m，埋置深度取1.0 m，全部埋入地基中；地基模型尺寸横截面为10 m×10 m，在基础表面施加1 t的正弦周期力，震源频率为10 Hz。根据具体试验测定情况，可选取如下参数：基础弹性模量8 600 MPa，泊松比0.3，基础密度2.0 g/cm3；地基弹性模量50 MPa，泊松比0.30，地基密度1.7 g/cm3。为便于计算，利用模型的对称性，建立1/4模型进行计算，地基模型四周设置透射边界，地基底面分别采用透射和固定约束两种边界条件。

图2动力基础有限元模型

3.2　计算结果

基础尺寸2.8 m×2.8 m×1.5 m，地基尺寸10 m×10 m×h，h为地基深度，基础全部埋入地基，地基底面分别采用透射和固定约束两种边界条件，并且把计算结果与理论结果进行对比分析以确定模型深度h。地基模型深度h选取20 m和40 m，地基底面分别采用透射和固定约束两种边界，计算结果见图3～图5。

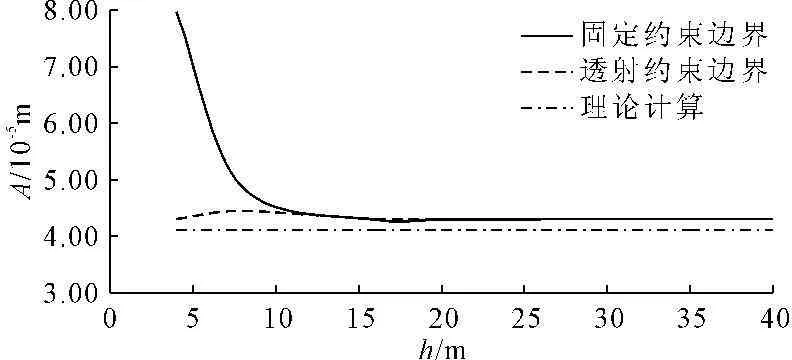
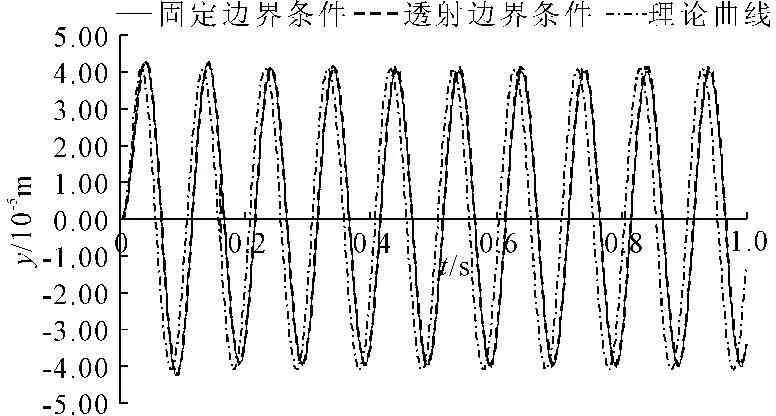
图3　两种边界条件下最大振幅随模型深度变化曲线

图4　h=20 m时基础表面平均位移随时间变化曲线

取地基模型深度为20 m，地基四周和底面均采用透射边界条件，在基础表面施加1 t的正弦周期力，频率为10 Hz。基础表面荷载分布形式和基础表面尺寸分别采取集中荷载和0.2 m×0.2 m，0.4 m×0.4 m，0.6 m×0.6 m，0.8 m×0.8 m，1.0 m×1.0 m，1.2 m×1.2 m等不同面积。取基础表面点作为位移控制点，计算结果见图6～图7。

图6　不同荷载分布形式下基础中心点位移随时间变化对比曲线

图7不同荷载分布形式下基础表面平均位移随时间变化对比曲线

取地基模型深度为20 m，地基四周和底面均采用透射边界条件，在基础表面施加1 t的正弦周期力，频率为10 Hz。荷载采用集中荷载形式，作用在全模型基础的几何中心点上。选取1/4模型基础表面四个角点以及几何中心点进行分析对比，所得结果见图8～图11。

图8　集中荷载形式下基础表面不同点平均位移随时间变化对比曲线

图9　不同横截面尺寸条件下基础表面平均位移随时间变化对比曲线

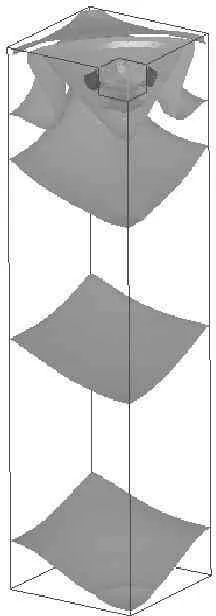
图10　Y方向主应力分布图

图11第一主应力分布图

3.3　结果分析

由图4、图5可得出，采用底面固定约束条件下，地基模型深度在20 m以内时，基础表面点的平均位移最大振幅值在第一个时间周期内均有不同程度的突变，突变程度随模型深度的增大而减小，地基模型深度在20 m～40 m变化时基础表面点的振幅随模型深度的增加基本不变，其值比较稳定，并且与理论值一致。在采用底面透射约束条件下，地基模型深度在15 m以内时，基础表面点的平均位移随时间变化曲线在整个时间周期内均有较小程度的向Y轴正方向偏移，而偏移量则随着地基模型深度的增加而减小。当模型深度在15 m～40 m变化时，基础表面点的平均振幅值基本保持不变，并且与理论值一致。通过图3～图5的对比分析，可得出地基模型深度在20 m至40 m变化过程中，分别采取固定边界和透射边界两种边界约束的条件下，基础表面点的平均位移值随时间变化曲线完全重合，与理论曲线的振幅和频率也基本一致，只是在时间上较理论曲线有较小的相位滞后性，并且这种滞后性随模型深度的增加而有所增加，与实际情况相符合。

由图3分析得出，当地基模型深度在不小于20 m的情况下，地基底面采用固定约束和透射约束两种方案的边界条件对基础表面点的平均振幅的影响基本没有区别，其值均与理论值保持一致，故地基模型深度取不小于20 m为宜；固定约束边界和透射约束边界对模型深度大于20 m时的基础表面点的平均位移曲线的影响基本没有区别，而当模型深度较小时，相对于固定边界条件，采用透射约束边界条件时基础表面点的平均位移曲线与理论曲线比较接近，故通常情况下采用透射边界条件计算的结果更接近实际情况。

通过图6得出，当模型深度为20 m时，集中和均布两种荷载分布形式下，基础表面中心点位移随时间变化曲线有着明显的突变。在集中荷载作用下，曲线的振幅值较均布荷载时大很多，并且曲线整体向Y轴正方向偏移，其振幅与频位均与理论曲线相差较大；当荷载形式为均布荷载时，在荷载分布面积由0.2 m×0.2 m至1.2 m×1.2 m的变化过程中，基础表面中心点的位移随时间变化曲线基本没有变化，并且均与理论曲线的振幅和频位保持一致。

通过图7得出，尽管荷载分布面积由集中到均布面积不断增大，但是基础表面所有点随时间变化的平均位移曲线却没有任何变化，并且其振幅和频位均与理论曲线保持一致。

由图8可以看出，在集中荷载形式下，基础表面不同点之间的位移随时间变化的曲线是不同的，其振幅和相位均相差较大，并且与理论曲线的振幅和相位也相差较大。

由图9分析得出，在基础横截面尺寸由0.2 m×0.2 m至1.2 m×1.2 m的增大过程中，基础表面平均位移的振幅值不断减小，在基础横截面尺寸达到1.0 m×1.0 m时，其曲线的振幅和频位均与理论曲线比较接近。

通过Y方向的应力分布云图图10和第一主应力分布云图图11的结果展示，可进一步说明本文数值模拟建模计算的正确性。

4结语

(1) 本文采用的研究动力机器基础设计的数值模拟方法是可行的，正确的。

(2) 在进行数值模拟过程中，采用求基础表面平均值的方法而计算出的几何中心的计算结果与理论计算结果是一致的，并且是正确的。

(3) 在进行数值模拟计算时，荷载的不同分布形式对基础表面的平均位移曲线的振幅和频位基本没有影响。

(4) 建模时，地基模型深度不小于20 m、基础模型横截面尺寸不小于1.0 m×1.0 m时，计算结果与理论结果基本一致。

(5) 通过应用数值模拟方法所得出的计算结果与通过Lysmer方程所得出的理论结果进行对比分析，进一步验证了Lysmer方程的正确性。

参考文献：

[1]严人觉，王贻荪，韩清宇.动力机器半空间理论概论[M].北京：中国建筑工业出版社，1981.

[2]王杰贤.动力机器与基础[M].北京：科学出版社，2001.

[3]朱伯芳.有限元法基本原理[M].北京：高等教育出版社，1987.

[4]谢定义.土动力学[M].西安：西安交通大学出版社，1988.

[5]刘晶波，王振宇，张克峰，等.考虑土-结构相互作用大型动力机器基础三维有限元分析[J].工程力学，2002(6)：34-38.

[6]蒋东旗，谢定义.动力机器基础设计的数值方法研究[J].土木工程学报，2002，35(1)：74-78.

[7]黄菊花，何成宏，杨国泰.地基中振动波传播的有限元分析[J].震动与冲击，1999，18(1)：38-43.

[8]王锡康.对地基动刚度及惯性作用的研究[J].岩土工程学报，1984，6(4)：75-85.

DOI:10.3969/j.issn.1672-1144.2015.04.031

收稿日期：2015-04-20修稿日期：2015-05-17

作者简介：朱飞(1984—)，男，陕西户县人，硕士，工程师，主要从事地质灾害防治工程的勘查和设计工作。E-mail: zhufeixl@qq.com。

中图分类号：TU470

文献标识码：A

文章编号：1672—1144(2015)04—0155—04

Comparison Between Numerical Simulation of Power Machine Foundation and Lysmer Analytical Method

ZHU Fei1, PENG Hongming1, LEI Youde1, CAO Chengming2

(1.QinghaiEnvironmentalGeologyExplorationBureau,Xining,Qinghai810007,China；2.GansuZhongjianMunicipalEngineeringSurveyandDesignInstitute,Lanzhou,Gansu730000,China)

Abstract：With the consideration of the basis and foundation being the entire elastic system, the models of the system with different foundation depth and size under different loads were simulated and analyzed using numerical methods. And then the results were compared with the calculation results of Lysmer equation. According to the study, the modeling conditions for correct numerical analysis are determined, and the integrity of Lysmer equation is verified.

Keywords:foundation of dynamic machine; elastic half-space; numerical method