大型地下洞室围岩稳定性数值模拟分析
2015-12-24鹿庆蕊AndreaPerino陈士军刘慧群
鹿庆蕊,Andrea Perino,赵 凯,陈士军,刘慧群
(1.东华理工大学 建筑工程学院,江西 南昌 330013; 2.都灵理工大学 结构岩土学院, 都灵 10129 意大利;3.南京工业大学 交通学院, 江苏 南京 211816; 4.同济大学 建筑设计研究院(集团)有限公司, 上海 200092)
大型地下洞室围岩稳定性数值模拟分析
鹿庆蕊1,Andrea Perino2,赵凯3,陈士军1,刘慧群4
(1.东华理工大学 建筑工程学院,江西 南昌 330013; 2.都灵理工大学 结构岩土学院, 都灵 10129 意大利;3.南京工业大学 交通学院, 江苏 南京 211816; 4.同济大学 建筑设计研究院(集团)有限公司, 上海 200092)
摘要:国内外水能资源的开发及大型地下古建筑群的保护往往需要布置地下厂房洞室群,而大型洞室的稳定性研究逐渐成为岩土工程学术界的研究热点。基于此,分别采用有限元软件Midas及离散元软件DEM对两大典型地下洞室的稳定性进行三维数值模拟分析:其一为位于意大利都灵省苏萨谷的Pont Ventoux水力发电站的Venaus洞室;其二为位于以色列的Tel Beer Sheva 洞室。 计算结果表明,根据围岩性状不同选取不同的计算工具均可较可靠的评价地下洞室的稳定性,且三维模型可更精确的描述洞室几何尺寸及围岩性状。
关键词:大型地下洞室;连续性;非连续性;数值方法
大型地下洞室的稳定性问题较为复杂,已引起工程界和学术界的广泛兴趣。近半个世纪以来, 随着计算机技术的日益发展以及力学、数学理论的不断完善,在工程地质和岩土工程领域数值分析方法得到了愈加广泛的应用, 并逐渐成为解决复杂边界条件下、复杂介质等各类工程问题不可或缺的重要工具[1-7]。
关于大型地下洞室稳定性分析的实例,文献[8-13]中已大量涉及。王思敬等(1984)运用有限元法进行洞室开挖稳定性模拟分析,研究了当间距不同时,新开挖洞室对主洞的影响[13]。Barton通过开展对最大跨径62 m的大型洞室稳定性进行数值模拟分析,进一步表明对于复杂形状的洞室,使用计算机数值模拟技术可相对精确地描述围岩的基本性状以及洞室的几何形状[12]。另一方面, 洞室稳定性数值分析最关键的环节之一,是岩体模拟方法的选择。当前,广泛应用的岩石洞室稳定性模拟数值方法主要有以下两种[14]:(1) 离散性数值建模方法,即将不连续岩体视为非连续介质。该方法中最重要的环节是描述岩体及节理的性状。同时,节理及不连续面在该方法中起着非常关键的作用,而岩体由通过节理相互联系的块体表示。因此节理和不连续面的几何特性如方向和间距的模拟同样不可忽视。(2) 等效连续性建模方法,该方法将岩体视为连续性介质,即岩体具有各向同性的性质,因此该介质(弹性,弹塑性等等本构)可用一种本构关系来定义。
本文将着重通过连续和离散性数值建模分别对两个典型大洞室进行稳定性模拟分析。首先采用有限元软件MIDAS/GTS对某大型水电站的中央Venaus洞室进行三维数值计算分析,随后采用离散元程序对Tel beer sheva洞室分别进行二维和三维数值分析,并进一步探讨两种模拟方法的可靠性。
1连续性数值建模
1.1 工程及数值模型概述
Pont Ventoux水力发电厂位于意大利都灵苏萨谷,具有非常复杂的几何构造格局,而其最大的枢纽洞室——Venaus中央洞室是发电厂复杂格局中最重要的组成部分(图1)。该水利发电厂由长为1 170 m的隧道经Venaus-Susa通道抵达洞室入口。Venaus中央洞室埋深约250 m,围岩主要由碳酸盐片岩组成。

图1Pont Ventoux-Susa 水电站系统之中央Venaus洞室布局图
由于Venaus洞室规模较大,长度50 m,最大高度约49 m,最大跨度23 m。故其开挖方法为分阶段爆破开挖。洞室支护系统主要由两部分系统组成,其一为被动短锚支护系统,在洞室施工过程中开挖洞室的同时安装支护系统,其二为永久性预应力锚杆支护系统,其在每个开挖阶段完成时安装,同时应施加预应力为其最终承载力的2/3[15]。
由于洞室的几何对称性(仅适用于本文的静力分析,不涉及后续的动力分析),本文利用有限元软件MIDAS/GTS仅对洞室的一半进行模拟分析。另一方面,由于选取对象Venaus洞室覆盖层较厚,埋深较大,故可认为该洞室处于远场原地应力作用。基于此,有限元所建立的三维数值模型几何尺寸为230 m×115 m×230 m,如图2(a)所示。根据该洞室最大断面的尺寸,其开挖分为12个阶段,每个阶段的最大开挖深度不大于5 m,并且在每个开挖步中伴随有厚度为2 m的开挖扰动层,如图2(b)所示。图2(c) 显示了分阶段安装的短锚被动支护系统和预应力锚杆永久支护系统。

图2Venaus洞室模型
Venaus中央洞室开挖支护阶段进程模拟简要概括如下:
(1) 远场原始地应力状态下的三维数值模型初始化。
(2) 模拟第一阶段开挖模拟,同时激活对应第一阶段开挖区周围2m扰动区并安装被动短锚支护系统。
(3) 模拟第二阶段开挖、激活其对应扰动区并安装被动短锚支护系统的同时,在第一阶段开挖区围岩安装永久性预应力锚杆支护系统并安装衬砌。
(4) 其他开挖阶段按照上述方式依次分阶段进行。
洞室围岩未扰动区、扰动区的Hoek-Brown常数为m=1.18,s=0.012及m=0.28,s=0.002;泊松比为0.25;未扰动区、扰动区的变形模量分别为22 GPa、14 GPa。同时,根据测定,静压力系数K0为0.56,竖向地应力为10.8 MPa。
1.2 计算结果分析
本文主要呈现了Venaus洞室分别在未加固和加固系统下的开挖稳定性,而由洞室在未支护以及支护体系下的最小主应力分布比较结果可以看出现有的支护系统较明显的减小最小主应力,换言之,本洞室所采用的支护体系可有效地预防拉裂的可能。
另外,洞室实际开挖施工过程中在最大截面洞顶点处安装了一套位移监测系统,以量测洞室开挖引起的洞顶竖向位移。图3为洞顶实测位移与模拟的未支护、支护条件下洞顶处的计算位移比较分布图,由图3可以看出,在距离洞室8 m范围内,由三维数值模拟计算的的位移低于实际监测位移,而8 m范围外,计算位移稍大于测量值,支护体系下的围岩变形显然小于未加固洞室截面变形。对比分析可进一步说明本文采用的三维有限元建模较为可靠。

图3洞室开挖引起的洞顶测量与计算位移分布
2离散性数值建模
2.1 工程及数值模型概述
选取的典型工程为位于以色列Negev沙漠的Tel Beer Sheva洞室工程。考古研究发现,该洞室大致开挖于3 000年前,推测为一大型水库的关键枢纽工程。该洞室几何构造形状极不规则(图4),围岩主要由裂隙型极软石灰石构成。地质勘察资料显示岩体主要由两个垂直不连续子节理组(平均间距为20 cm和25 cm)和水平不连续层理面(平均间距50 cm)组成。据现场勘察资料推测,洞室在最初的开挖阶段历经了洞顶倒塌灾害。鉴于此,在洞室中心建立了中央柱以进一步确保洞室的稳定性。自此洞室历经3 000年以来数次的地震动,但并未遭受较大的地震灾害。
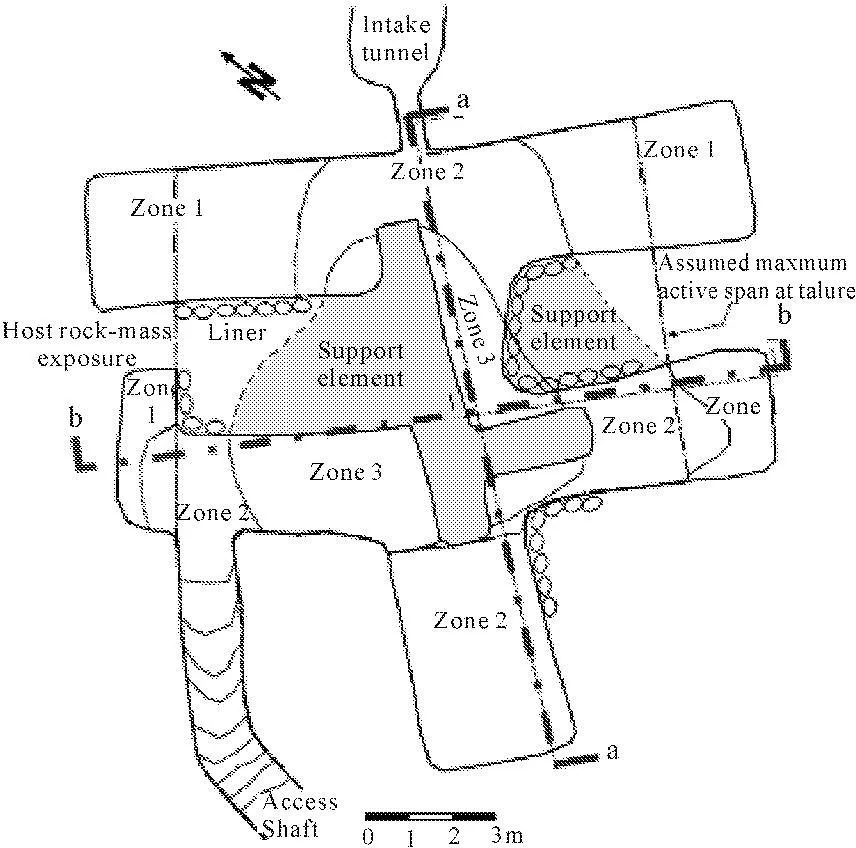
图4洞室平面布局图
本分析采用离散性计算软件3DEC(Itasca consulting group)对洞室进行无中央柱、有中央柱情况下的稳定性数值模拟分析。建立的洞室三维模型尺寸为45 m×45 m×23 m。洞室覆盖层约为13 m。图5(a)、图5(b)分别为无、有中央柱的洞室三维轮廓图,其中图5(b)洞室中空的部位为中央柱支护。洞室完整岩石的泊松比为0.1,杨氏模量为2 GPa,重度为19 kN/m3,其他离散性力学参数见表1。本洞室模型本构关系采用弹塑性的莫尔库仑理论进行研究。
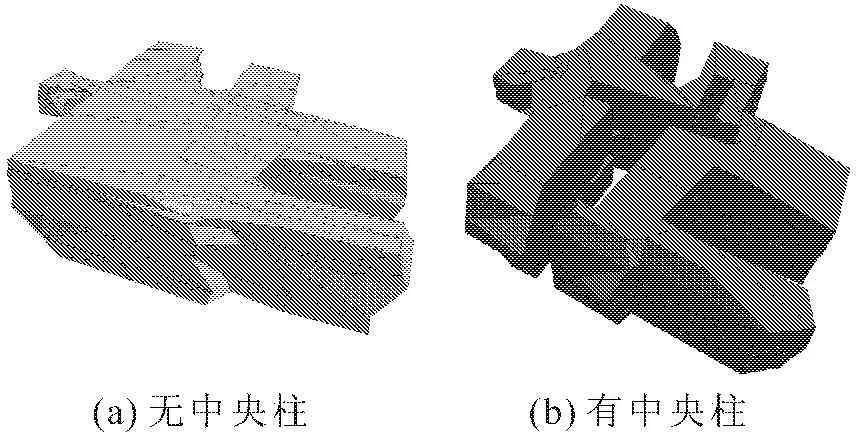

图5 Tel Beer Sheva洞室三维轮廓图
其中,knn为法向刚度,kss为切向刚度。
2.2 计算结果分析
图6所示为无中央柱模型对应图4的两个主要横截面a-a、截面b-b的反分析结果。两截面最大跨径分别为12.8 m和15.0 m。同时图6中还显示出三维、二维数值计算[16]以及现场勘测的洞顶塌陷变形的对比。为获得合理的离散性力学参数,数值反分析法允许对数值模型进行多次校核。静水压力系数K0为0.5,可由二维数值模拟的洞顶崩塌反推而得。而通过3D数值模型模拟洞室顶板坍塌,经过多次数值计算分析表明,应当将静水压力系数K0减小到0.3。这是由于与二维平面应变分析相比较,三维数值模拟分析还需考虑各个水平方向的拱效应及平面外的约束。在三维数值模拟洞室顶板坍塌的进程中,拱下岩块压缩应力逐渐减小,直至洞顶坍塌破坏。
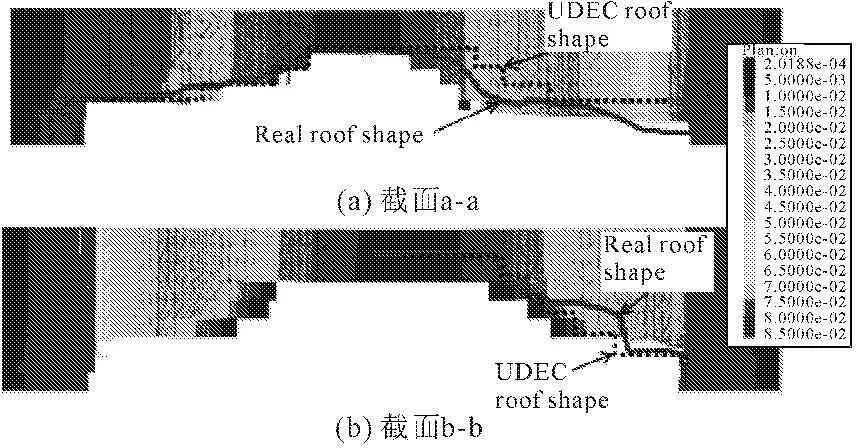
图6二维、三维以及现场测得的洞顶倒塌时的变形
鉴于上述,与二维平面应变分析相比较,三维数值建模可以更可靠地评价大型地下空间稳定性。同时可进一步得出:静水压力系数K0、不连续面的排列和间距和平面外的拱效应为影响该洞室稳定性的关键因素。该结论也可由文献[17]相关研究结果所验证。另外,计算结果还表明保持静水压力系数为0.5同时减少垂直节理的摩擦角到最小(35.8°),并没有显著影响洞室稳定性。因此进一步佐证了洞室的稳定性主要由K0和洞室的拱效应所控制。
3结论
选取两种不同的典型大型洞室为研究对象,通过现场测量与连续和离散性建模数值计算结果相比较,可分别验证本文所采用的两种不同的建模方法的可行性。特别是,采用连续性3D建模可对Pont Ventoux水力发电厂的中央Venaus洞室各阶段开挖和支护进程进行较为精确的模拟,并可考虑开挖扰动区的性状和稳定性。通过离散性数值建模可再现Tel Beer Sheve洞室顶板的塌陷过程。因此,具体数值模型的选择依赖于围岩的基本性状及涉及的具体工程问题。
参考文献:
[1]潘别桐,黄润秋.工程地质数值法[M].北京:地质出版社,1994.
[2]朱合华,陈清军,杨林德.边界元法及其在岩土工程中的应用[M].上海:同济大学出版社,1997.
[3]雷晓燕.岩土工程数值计算[M].北京:中国铁道出版社,1999.
[4]潘昌实.隧道力学数值法[M].北京:中国铁道出版社,1995.
[5]谢康和,周健.岩土工程有限元分析与理论[M].北京:科学出版社,2002.
[6]刘宁.可靠度随机有限元法及其工程应用[M].北京:中国水利水电出版社,2001.
[7]王泳嘉,邢纪波.离散单元法及其在岩土工程中的应用[M].沈阳:东北工学院出版社,1991.
[8]杨淑清.地下洞室围岩开挖稳定性分析[J].武汉水利电力学院学报,1986(2):73-82.
[9]陈霞龄,韩伯鲤,梁克读.地下洞群围岩稳定的试验研究[J].武汉水利电力大学学报,1994(1):17-23.
[10]赵震英,叶勇.复杂地质条件下地下洞室围岩应力及变形模拟试验研究[J].岩石力学与工程学报,1989,8(4):298-305.
[11]陶连金,王泳嘉,张淖元.大倾角煤层开采矿山压力显现及岩层控制[M].成都:四川科技出版社,1998.
[12]Barton N, By T L, Chryssanthakis P. Tunbridge, et al. Predicted and measured performance of the 62 m span Norwegian olympic ice Hockey Cavern at Gjcvik[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics, 1994,31(6):617-641.
[13]王思敬,杨志法,刘竹华.地下工程岩体稳定分析[M].北京:科学出版社,1984.
[14]Barla G, Barla M. Continuum and discontinuum modelling in tunnel engineering[J]. Gradevinar, 2000,52(10):563-576.
[15]Barla G, Fava A, Peri G. Design and construction of the Venaus powerhouse cavern in calcschists[C]//Italy: FELSBAU, 2008:399-406.
[16]Barla G, Monacis G, Perino A, et al. Distinct element modelling in static and dynamic conditions with application to an underground archaeological site[J]. Rock Mechanics and Rock Engineering, 2010,43(6):877-890.
[17]Hatzor Y H, Benary R. The stability of a laminated voussoir beam: back analysis of a historic roof collapse using DDA[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics, 1998,35(2):165-181.
DOI:10.3969/j.issn.1672-1144.2015.04.027
收稿日期:2015-03-21修稿日期:2015-04-24
基金项目:江西省自然科学基金项目(20142BAB216005);江西省科技支撑计划(20151BBG70004);东华理工博士启动金项目(DHBK2013203);国家自然科学基金项目(51468001)
作者简介:鹿庆蕊(1984—),女,博士,讲师,主要从事洞室开挖及抗震方面的研究工作。 E-mail:qingruilu@ecit.cn
中图分类号:TU457
文献标识码:A
文章编号:1672—1144(2015)04—0137—04
Numerical Analysis on the Stability of Large Scale Underground Caverns
LU Qingrui1, PERINO Andrea2, ZHAO Kai3, CHEN Shijun1, LIU Huiqun4
(1.FacultyofCivilandArchitecturalEngineering,,EastChinaInstituteofTechnology,Nanchang,Jiangxi330013,China;2.DepartmentofStructuralandGeotechnicalEngineering,PolytechnicUniversityofTurin,Turin,Piedmont10129,Italy;3.CollegeofTransportationScience&Engineering,NanjingTechUniversity,Nanjing,Jiangsu211816,China;4.TongjiArchitecturalDesign(Group)Co.,Ltd.,Shanghai200092,China)
Abstract:With the development of water resources utilization and the protection of ancient underground architecture, it is necessary to construct relevant large scale underground projects. Recently great attention has been paid to the stability of large underground caverns in the research area of rock mechanics and rock engineering. In view of this, the numerical simulation on the stability of two typical large underground caverns was carried out. Following a brief introduction of the main modeling approaches, the analysis of the stability of cave Venaus by a continuous FEM model was firstly performed. The stability of cave Tel Beer Sheva was analyzed by constructing a discontinuous DEM model. The comparison of the results obtained by numerical analysis with the values measured in-situ validated the reliability of these two different modeling approaches of large scale underground structures excavated in rock mass, and it also proves that 3D model is able to better capture the features of complex projects.
Keywords:large scale underground cavern; continuous; discontinuous; numerical simulation
