高温引水隧洞应力场分布的研究

刘春龙，张永生，袁继国，钟　源，张　耀

(1.西安理工大学 岩土工程研究所， 陕西 西安 710048； 2.中交天津航道局有限公司， 天津 300000 3.西部机场集团， 陕西 西安 710075； 4.陕西煤田地质勘查研究院有限公司， 陕西 西安 710000)

高温引水隧洞应力场分布的研究

刘春龙1，张永生2，袁继国1，钟源3，张耀4

(1.西安理工大学 岩土工程研究所， 陕西 西安 710048； 2.中交天津航道局有限公司， 天津 300000 3.西部机场集团， 陕西 西安 710075； 4.陕西煤田地质勘查研究院有限公司， 陕西 西安 710000)

摘要：研究高温隧洞在温度稳定时，达到热平衡条件下的温度场及其引起的温度应力与隧洞自重应力的耦合分布形式。通过应用弹性力学中无限长圆筒对称温度应力的解析解与有限差分软件对温度场的分析，得出温度场及隧洞径向应力σρ、环向应力σφ和轴向应力σz的分布形式，表明在变温区，径向应力σρ呈先增大后减小趋势，环向应力σφ沿着洞径方向由拉应力变化为压应力，轴向应力σz沿着洞径方向为压应力增大。模拟温度应力与自重应力耦合作用下在隧洞水平边墙和洞室顶部的应力分布规律。表明在两个不同位置处的耦合应力分布明显不同，环向应力σφ在水平边墙处为压应力，且逐渐增大后趋于稳定，而在隧洞顶拱处为拉应力，逐渐变为稳定温度区的压应力。隧洞洞顶拱处的混凝土衬砌在耦合应力作用下处于拉应力状态，在环向拉应力作用下极易产生裂缝。

关键词：高温隧洞；温度分布；应力分布；数值分析；耦合分析

随着我国基础设施的不断建设和发展，尤其对于我国西南山区的基础建设，经常会遇到由于复杂的工程环境所带来的各种各样的难题。特别是水利水电工程建设以及地下工程的开发与利用，不良的地质条件和突发性问题经常发生，给工程的设计施工以及运营带来严重影响。目前，我国在建的水工隧洞洞室围岩温度一般多为15℃～30℃，根据国内有关资料，当地温超过30℃时称为高地温[1]。地下洞室的开发与修筑过程中难免会遇到高温高地应力的情况，而高温不仅为施工的过程带来极大地困难与不便，也为施工人员的安全带来隐患，同时由于高温产生的温度应力也是工程的一大难题。

随着温度因素导致的工程问题越来越多，人们对于温度的作用逐渐了解。近年来，国内外学者对温度问题进行了大量的试验与理论研究。李宁等[2-3]对岩体介质、土体介质的温度场、变形场和渗流场，构建了多场多相介质的理论框架。张岩等[4]对高温隧洞稳定性的多因素进行了分析，得出了初始温度场的温度越高或温度差越大、围岩类别越好，围岩的温度应力越大。张先军[5]对青藏铁路昆仑山隧道洞内气温及地温分布特征进行研究，得出了该隧道洞内气温、地温及隔热层内外侧的温度分布特征。刘乃飞等[6-8]对布伦口水电站高温引水发电隧洞的受力特性进行了研究，采用稳态和瞬态两种方法分析了温度分布规律。和学伟等[9-13]对黑白水三级电站高温高压热水条件下的引水隧洞施工进行了介绍，指出 在此条件下隧道施工必须采取综合降温措施。焦国锋等[14-16]对拉萨至日喀则(拉日)铁路高地温的分布特征进行研究，指出产生高温地热的原因，为铁路隧洞的施工与运营提供了参考意见。本文对娘拥水电站引水隧洞K0+972—K1+052段在超高地温条件下，洞室开挖后围岩温度稳定平衡阶段的温度分布及温度应力场与自重应力场的耦合应力分布形式进行研究，并对洞室顶拱衬砌开裂进行解释。对实际工程具有一定的参考意义。

1工程概况及计算模型

1.1　工程概况

娘拥水电站位于四川省乡城县境内，属于云贵高原与青藏高原的过渡地带，地貌上为典型的构造剥蚀类型的高原山地，地形多以条形山体为主，其构造强烈，不同地段构造应力明显不同。该水电站属于硕曲河干流梯级开发的梯级电站，装机容量为93 MW，电站引水隧洞全长15.406 km。设计顶拱半径为4.0 m。引水隧洞共设置7条施工支洞，其中隧洞在K0+972—K1+052段穿过热水断层，受热水断层的影响1#施工支洞及引水隧洞的施工期间洞室内温度异常，环境温度高达43℃，岩石表面温度达58℃，涌水温度为82℃，爆孔内温度达48℃～76℃，从勘察设计单位已监测的温度数据得出，洞壁外16 m最高温度可达105℃。洞室水平埋深约170 m～1 600 m，上部垂直埋深一般在150 m～500 m，最大埋深640 m。高地温洞段初期支护环境与常规施工环境存在很大的差异，对锚杆的拉拔力、混凝土的厚度与强度等常规工艺影响较大。二次衬砌施工时，由于混凝土内外温度差较大，加之高温围岩对混凝土水分的吸收，使混凝土衬砌极易造成表面开裂，尤其洞室顶拱衬砌产生不均匀裂缝明显。因此，施工时尽可能的控制混凝土浇筑的环境温度与入仓温度并缩短浇筑长度和作业时间。二次衬砌拆模后测得混凝土表面温度为45℃。

1.2　计算模型

根据工程背景，模型隧洞为圆形断面，开挖洞径为8.0 m，根据施工揭示的地质情况，洞内干燥，未见地下水出露，个别裂隙中有热泉涌出。因此，考虑地下水位的影响，温度距离洞中心轴线20 m处趋于稳定，取半径的7.5倍作为研究区域。模型洞室内存在与外界的热交换为第二类边界条件，λ(∂T/∂n)s=(qn)s=f(t)，模型外部围岩温度趋于稳定为第一类边界条件Ts=C，地质勘查报告及现场实测资料可知该洞室的热学参数为：导热系数8.0 W/(m·℃)，岩体比热取760 J/(kg·℃)，线膨胀系数取为5.6×10-6(1/K)。模型下部边界为固定边界，两侧边界为法向水平约束，上部边界为自由边界条件。荷载及边界条件的分析几何模型如图1所示。岩体力学参数如表1所示。

图1　分析模型几何关系图

2温度场的计算与分布

2.1　温度场与温度应力理论分析

根据弹性力学热传导微分方程，如果物体没有内热源，当热流稳定以后，微分方程变温T应当满足微分方程2T=0。

(1)

微分方程(1)求得：T=Alnρ+B，由边界条件，可以求得任意常数A与B。得出温度变化函数T。进而径向应力σρ、环向应力σφ和轴向应力σz的大小。理论得出的温度场分布、径向应力、环向应力、轴向应力的分布规律如图2～图5所示。

(2)

(3)

(4)

(5)

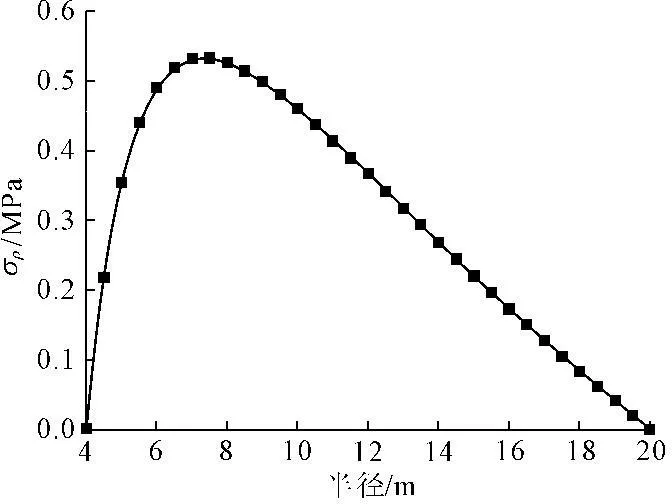
图2　理论温度场分布规律曲线

图3　理论径向应力分布规律曲线

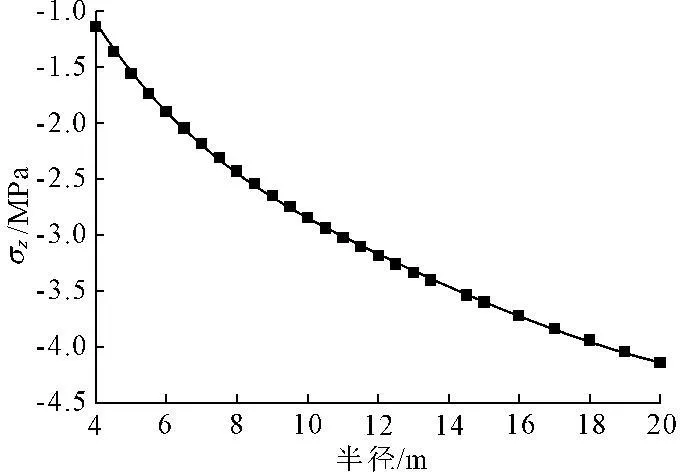
图4　理论环向应力分布规律曲线

图5理论轴向应力分布曲线

式中：a为内半径；b为外半径；ρ为温度区域内任意一点到隧洞中轴线的距离；Ta为隧洞内壁温度；Tb为洞壁外稳定温度。

2.2　温度场与温度应力数值分析

采用FLAC3D数值分析软件对隧洞围岩变温区温度场进行模拟，分析模型尺寸如图1所示，岩体参数见表1。由数值分析模拟得出的数值解温度场分布曲线如图6所示，图7为模拟得出的数值解径向应力σρ变化曲线，图8和图9分别为数值解得围岩温度稳定平衡时变温区环向应力σφ和轴向应力σz的关系曲线。

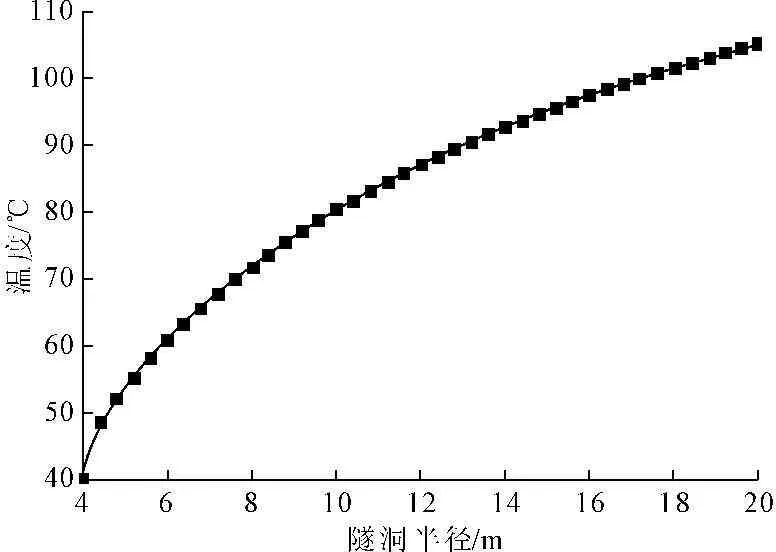
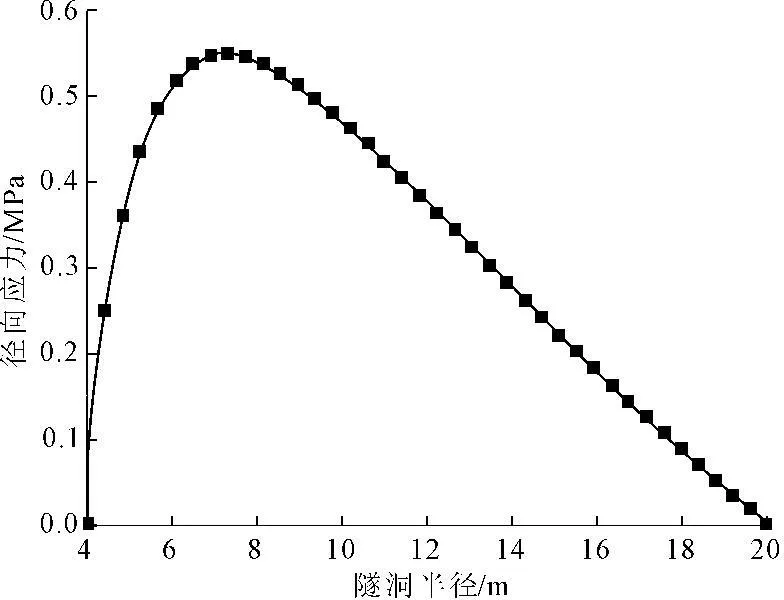
图6　数值解温度场分布规律曲线

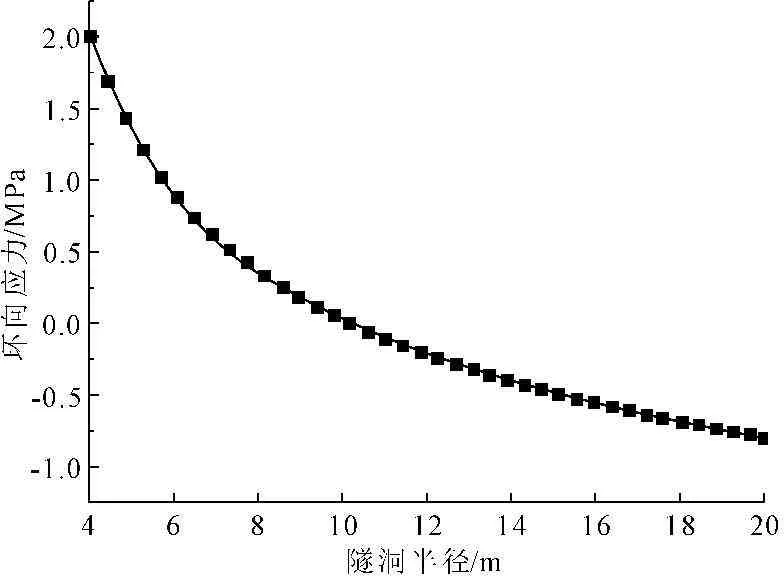
图7　数值解径向应力分布规律曲线

图8数值解环向应力分布规律曲线

从图2与图6中可以看出，由解析解与数值解得出的温度分布曲线几乎一致，围岩温度沿径向距离的增加而逐渐增大。隧洞径向应力如图3与图7所示，可以看出理论计算与数值模拟的结果几乎完全一致，在内外边界处径向应力为0，随着径向距离的增加，温度所引起的径向应力先增大而后减小，当径向距离为7.5 m时达到最大值为0.53 MPa。图4与图9分别为理论与数值模拟计算出来的环向应力随半径距离的变化，可以看出，环向应力随径向距离的增加由拉应力逐渐转化为压应力，转折点位于10.2 m处，围岩最大环向应力发生在隧洞内壁处，为拉应力2.2 MPa，温度稳定处的环向应力为压应力0.8 MPa。由图5与图9可以看出，隧洞轴向应力沿着洞径方向由隧洞内壁向隧洞外逐渐增加，隧洞内壁轴向应力最小，为压应力1.14 MPa。

3围岩耦合应力分析

3.1　水平围岩应力耦合分布

隧洞围岩体真实的受力应该包括，稳定平衡温度场引起的温度应力和围岩自重场引起的自重应力的耦合，本文不考虑隧洞运营期的内水压力作用。而温度场与重力场的耦合不是简单的两者应力的叠加，而是两者相互影响相互作用的应力结果。因此，采用数值分析法对两场进行耦合分析。得出隧洞水平边墙应力耦合分布规律，图10为洞室水平边墙径向应力σρ耦合分析结果，图11和图12分别为环向应力σφ和轴向应力σz耦合结果关系曲线图。隧洞岩体力学参数见表1。

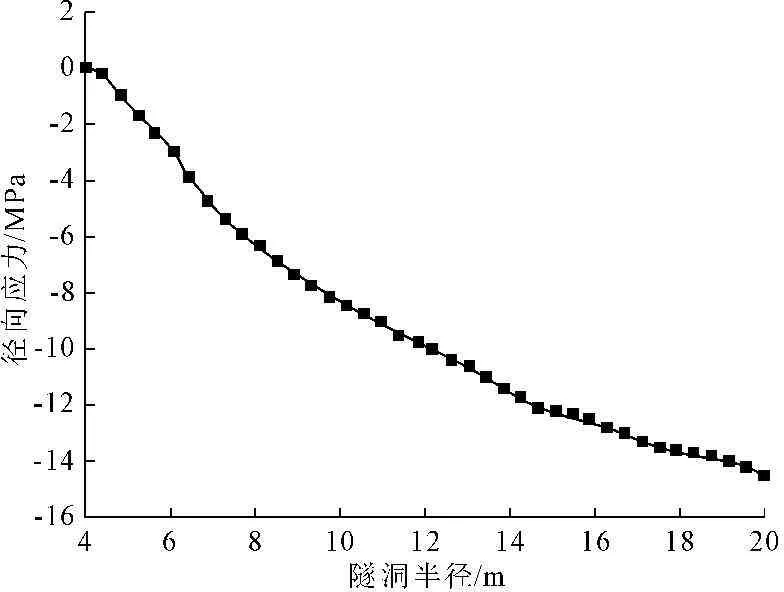
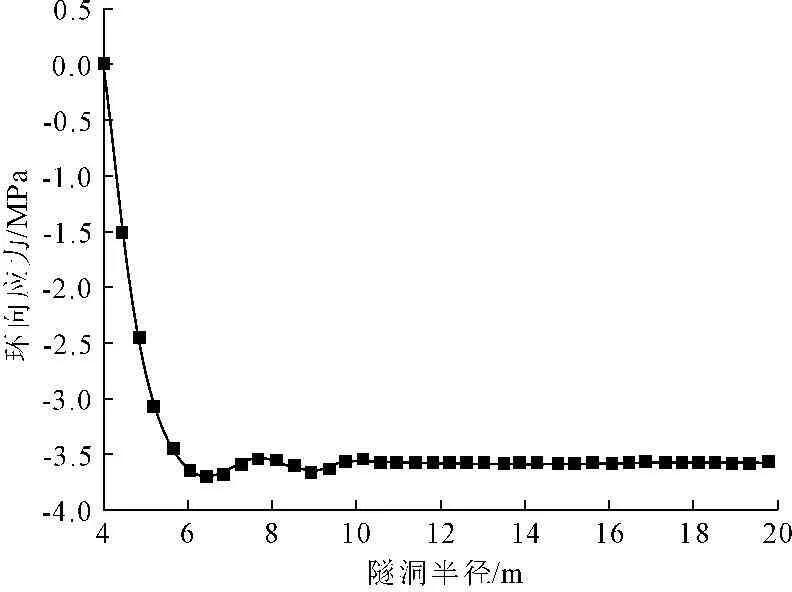
图10　径向应力耦合关系曲线

图11环向应力耦合关系曲线

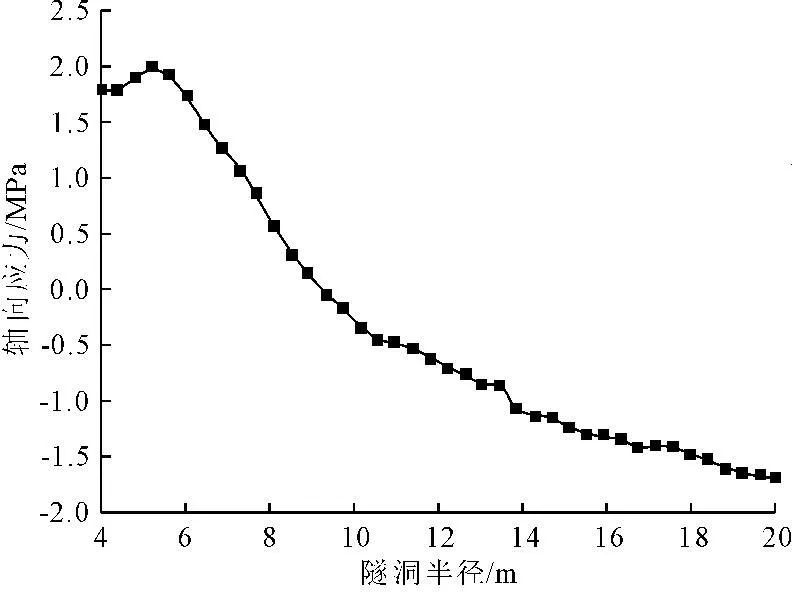
图12轴向应力耦合关系曲线

从图10可以看出，在温度应力与自重应力耦合下隧洞径向应力σρ随着径向距离的增加而逐渐增大，当径向距离达到稳定温度边界处时径向应力达到最大值为14.2 MPa。从图11可以看出，环向应力σφ随着围岩径向距离的增加而增大，在10.0 m处达到最大值，而后环向压应力趋于稳定。从图12可以看出，轴向应力σz的变化分布规律，轴向应力先由拉应力变为压应力，在6.0 m处拉应力达到最大值为0.16 MPa，在20.0 m处压应力达到最大值1.69 MPa，而后逐渐降低最后趋于稳定。

3.2　洞顶应力耦合分布

隧洞洞室顶部围岩的应力分布与水平围岩的应力分布完全不同，其原因是由于温度而产生的温度应力在洞室围岩的分布是各向同性的，而自重应力在洞室围岩周围产生的应力场分布明显不同。

图13为洞顶处围岩的径向应力σρ的分布规律，从图13中可以看出，洞室围岩内壁处于拉应力状态，大小为0.025 MPa，在洞径距离为5.0 m处的围岩拉应力最大，达到0.038 MPa，而后径向应力σρ由拉应力逐渐变为压应力，6.0 m处为拉压应力的转折点，压应力最大值位于11.5 m围岩处为0.22 MPa，最后压应力逐渐降低。图14为环向应力σφ的应力分布规律，可以看出，环向应力σφ由洞室围岩内壁处的拉应力0.51 MPa逐渐变为稳定温度区的压应力0.045 MPa，转折点位于洞径距离8.2 m围岩处。图15为轴向应力σz的分布规律，其变化规律为由洞室洞壁处所受的最大压应力逐渐变为拉应力。

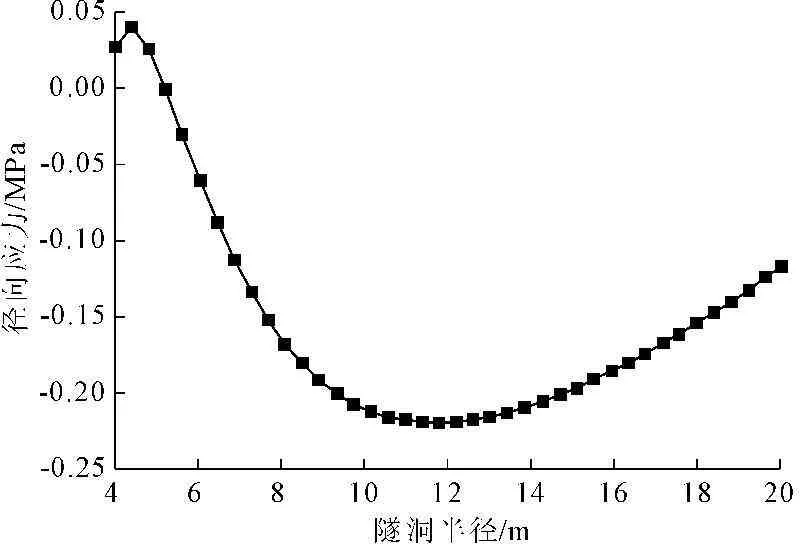
图13　径向应力耦合关系曲线

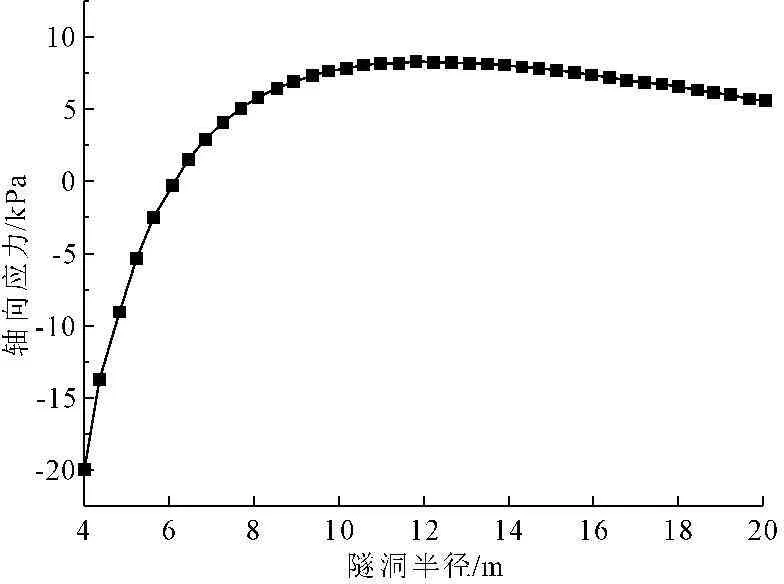
图14　环向应力耦合关系曲线

4衬砌应力分析

隧洞顶拱处衬砌耦合应力分布如图16和图17所示，可以看出，随着径向距离的增加，衬砌径向耦合应力呈先增大后减小趋势，在衬砌厚度中部达到最大为拉应力0.1 MPa。衬砌环向耦合应力随着径向距离的增加而线性减小，隧洞内壁处应力值最大达7.25 MPa，远大于混凝土的抗拉强度，即使在有钢筋的作用下，也很容易产生拉裂缝。同时，由于高温围岩对混凝土水分的吸收与蒸发，同样也会加重衬砌裂缝的产生。

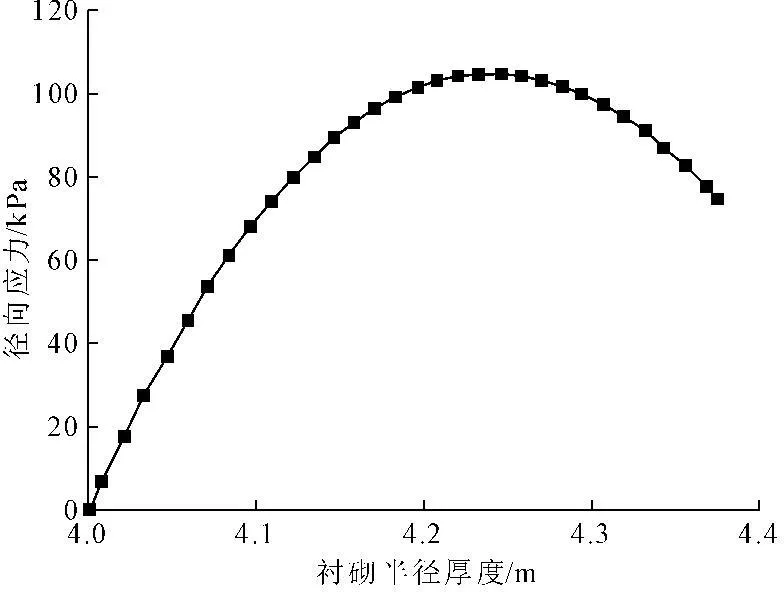
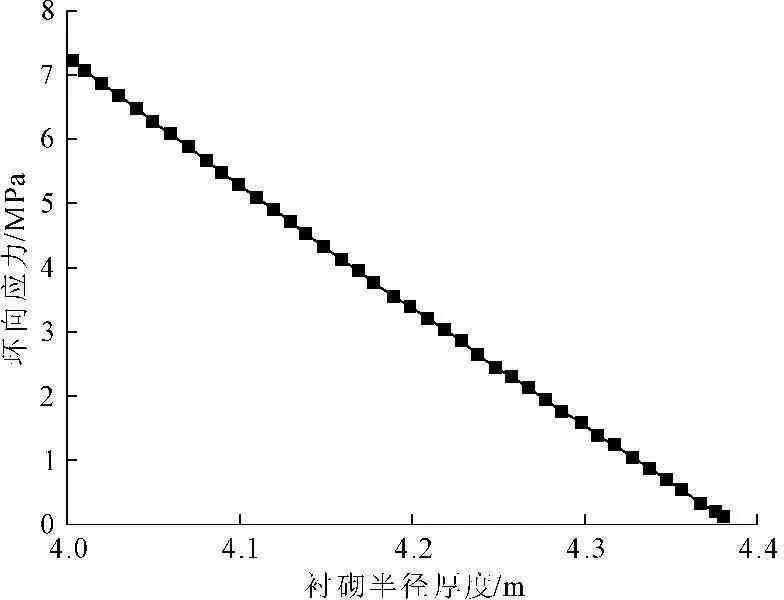
图16　衬砌径向应力耦合关系曲线

图17衬砌环向应力耦合关系曲线

5结论

本文基于娘拥水电站引水隧洞，对超高地温的温度场和应力场分布进行了分析，得出了稳定温度场条件下的洞室围岩温度分布及温度应力的分布形式，变温区温度场与洞室围岩自重应力场的应力耦合关系曲线。同时计算出高温隧洞条件下衬砌顶拱容易产生裂缝的模拟分析。通过分析得出以下结论，对工程设计、施工与运营具有一定的参考意义。

(1) 变温区所引起的温度应力分布为，径向应力σρ在洞壁处与稳定温度处为0，中间处应力值最大且为拉应力。环向应力σφ为沿着洞径方向由拉应力逐渐变为压应力，拉压应力的转折点在10.2 m处。轴向应力σz的分布为洞室内壁处应力值最小，沿着洞径方向压应力越来越大。

(2) 温度场与自重应力场耦合的洞室围岩应力分布在水平边墙处的分布规律与隧洞洞顶处的应力耦合分布明显不同。环向应力σφ在水平边墙处为压应力，且压应力逐渐增大后趋于稳定，而在隧洞顶拱处为拉应力0.51 MPa，逐渐变为稳定温度区的压应力0.045 MPa，转折点位于8.2 m处。

(3) 隧洞洞顶拱处的混凝土衬砌在耦合应力作用下处于拉应力状态，在环向拉应力作用下极易产生裂缝，加之高温围岩对混凝土水分不可避免的吸收与蒸发下，导致隧洞顶拱处产生不规则裂缝。

参考文献：

[1]袁培国.超高地温条件下引水隧洞施工关键技术探讨[J].水利水电技术，2014，45(4)：101-106.

[2]李宁，徐彬，陈飞熊.冻土路基温度场、变形长和应力场的耦合分析[J].中国公路学报，2006，19(3)：1-5.

[3]李宁，程国栋，谢定义.西部大开发中的岩土力学问题[J].岩土工程学报，2001，23(3)：268-272.

[4]张岩，李宁.多因素对高温隧洞稳定性的影响[J].西北农林科技大学学报：自然科学版，2012，40(2)：219-234.

[5]张先军.青藏铁路昆仑山隧道洞内气温及地温分布特征现场试验报告[J].岩石力学与工程学报，2005，24(6)：1086-1089.

[6]刘乃飞，李宁，余春海，等.布伦口水电站高温引水发电隧洞受力特性研究[J].水利水运工程学报，2014(4)：14-21.

[7]侯代平，刘乃飞，余春海，等.新疆布伦口高温引水隧洞几个设计与施工的探讨[J].岩石力学与工程学报，2013，32(S2)：3396-3404.

[8]刘乃飞.水-热-力三场耦合平台的验证与应用研究[M].西安：西安理工大学，2012.

[9]和学伟.高温高压热水条件下的引水隧洞施工[J].云南水力发电，2003(增1)：59-61.

[10]李占先.娘拥水电站引水隧洞超高地温段综合施工技术[J].水利水运工程学报，2014(4)：14-21.

[11]宿辉，张宏，耿新春，等.齐热哈嗒尔高地温引水发电隧洞施工影响分析及降温措施研究[J].隧道建设，2014，34(4)：351-355.

[12]苟彪，张军平.秦岭特长隧道_线平导施工降温措施的现场监测和研究分析[J].铁道工程学报，1999(1)：50-53.

[13]李湘权，代立新.发电引水隧洞高地温段施工降温技术[J].水利水电技术，2011，42(2)：36-41.

[14]焦国锋.拉萨-日喀则铁路高地温分布特征研究[J].铁道建筑，2013(8)：101-104.

[15]陈尚娇，黄润秋.深埋隧洞地温场的数值模拟研究[J].地质灾害与环境保护，1995(2)：30-36.

[16]朱珍德，李道伟，蒋志坚，等.温度循环作用下深埋隧洞围岩细观结构的定量描述[J].岩土力学，2009，30(11)：3237-3241.

DOI:10.3969/j.issn.1672-1144.2015.04.013

收稿日期：2015-01-14修稿日期：2015-07-10

基金项目：国家自然基金重点资助项目(05JS34)

作者简介：刘春龙(1989—)，男，黑龙江哈尔滨人，博士研究生，主要从事岩石力学试验研究方面的工作。E-mail：553925464@qq.com

中图分类号：TV672+.1文献标识码： A 文章编号： 1672—1144(2015)04—0066—06

Study on the Distribution of Stress Field in High-temperature Diversion Tunnels

LIU Chunlong1, ZHANG Yongsheng2, YUAN Jiguo1, ZHONG Yuan3, ZHANG Yao4

(1.InstituteofGeotechnicalEngineering,Xi'anUniversityofTechnology,Xi'an,Shaanxi710048,China；2.CCCCTianjinDredgingCo.Ltd.,Tianjin300000,China; 3.ChinaWestAirportGroup,Xi'an,Shaanxi710075,China;4.ShaanxiCoalfieldGeologyInvestigationResearchInstituteCorporation,Xi'an,Shaanxi710000,China)

Abstract：This research focuses on the coupling distribution of temperature stress caused by temperature field and tunnel gravity stress under the thermal equilibrium condition when the temperature in the high temperature tunnel reaches plateau and stabilizes. The distribution of the radial stress, circular stress and axial stress of the temperature field and the tunnel were obtained through the infinite long cylindrical symmetry temperature stress analytical solutions based on elastic mechanics and the analysis of temperature field by finite difference software. The results showed that in the temperature variation zone, the radial stress first increased and then decreased, the circular stress changed from tensile stress to compressive stress towards the direction of the tunnel, axial stress posed as the increasing compressive stress along the direction of the tunnel. And then the stress distribution of the level tunnel wall and the ceiling under the coupling action of temperature stress and gravity stress was simulated. It was found that the coupling stress distribution at the two different locations were totally different. The circular stress presented as compressive stress at the level wall, and it increased then stabilized, while at the arch of the ceiling it presented as tensile stress and then changed gradually into compressive stress at the stable temperature zone. Under the coupling stress, the concrete lining at the ceiling arch was under tensile stress, it would crack easily when under circular tensile stress. This analysis has some referential significance to the practical engineering.

Keywords:high temperature tunnel; temperature distribution; stress distribution; numerical analysis; coupling analysis