极值指数估计在太原站月降水频率分析中的应用研究

李　扬

(山西省水利水电科学研究院， 山西 太原 030002)

极值指数估计在太原站月降水频率分析中的应用研究

李扬

(山西省水利水电科学研究院， 山西 太原 030002)

摘要：在介绍极值理论基础、重尾分布判别方法的基础上，选用3种常用极值指数估计量，以山西省太原站月降水序列为例研究极值指数估计方法在月降水频率分析中的应用。结果表明：太原站月降水序列的样本分布属于重尾分布；选取序列强降水部分进行拟合时，Moment估计量对该段经验点据的拟合效果相对最佳，且计算简便，可为当地月降水序列的频率分析提供参考。

关键词：极值指数；月降水序列；Hill估计量；Pickands估计量；Moment估计量

暴雨、洪水、干旱等极值水文事件对人类社会的危害巨大。近年来，这类极值事件不断发生，制约了社会经济发展，威胁人民生命财产安全。因此，揭示极值事件中蕴含的统计规律十分必要。丁裕国[1]指出，相对正态分布而言，月降水量的概率分布呈偏态，极端降水的变化主要取决于其概率分布的尾部特征。邹波[2]的研究表明，月降水量的概率分布是一种重尾分布，分布尾部偏厚使得常用概率分布难以拟合强降水部分，导致对强降水事件发生的概率估计不足。因此，定量描述极值事件分布的尾部特征及估算极值事件的分位数，对研究极值事件统计规律、合理估计极值事件发生概率具有重要意义。

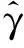
极值指数的估计和应用在金融领域应用较为成熟和普遍，而在水文学领域应用不多。因此，本文将极值指数引入降水事件的研究，并以山西省太原站为例，探讨了极值指数估计及设计值计算在月降水序列频率分析中的应用。

1极值理论基础

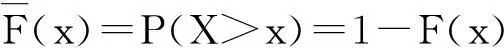
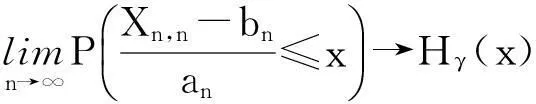
(1)

(2)

则分布F∈Fmda(Hγ)，MDA为最大吸引域(maximumdomainofattraction)。γ即为分布F的极值指数，可用于描述分布的重尾程度，即给定概率分布情况下极值事件的极端程度和频繁程度。

1.1　极值指数γ的估计量及相应极值分位数

极值指数γ的准确估计是拟合分布尾部的关键，决定着极值事件分位数的估计量理想与否。目前，国外学者提出了γ的多种估计量，常用的估计量有Hill估计，Pickands估计、Moment估计等。

1.1.1Hill估计[15]

(3)

式中，X1,n≤X2,n≤…≤Xn,n为X1，X2，…，Xn的次序统计量，k为所选取的极大次序统计量的个数。当超过概率p接近0时，极值分位数为

(4)

Hill估计容易实现且渐近无偏，在实际中最为常用，但当分布与Pareto分布相差较远时会导致Hill估计的偏差较大。

1.1.2Pickands估计[16]

(5)

当超过概率p接近0时，极值分位数为：

(6)

Dekkers和DeHaan[17]指出：k值对Pickands估计量及其相应分位数的影响很大，不适宜用于中小型样本。Dekkers等[18]和Drees[19]也指出了Pickands估计量的不稳定性。

4个组别的温度升高2 h后，采用瞬时扫描采样的方法，根据肉鸡不同的休息姿势，将肉鸡的收集行为划分为3类：第一类为坐姿，肘关节或胸部附着在地面或笼底，头悬于颈上静止不动或者有轻微的摆动；第二类为伸展，肉鸡身体一侧的一个翅膀伸展或一条腿伸展不动；第三类为俯伏，肉雏鸡表现为胸部附着在笼底部，并且颈部在地面或笼底部不动或者头斜向伸长，张嘴呼吸。肉鸡行为指标测定，在温度升高2 h后进行，由专人连续观察10 min，在进行数据分析时，行为频数百分比为该休息行为发生频率占总休息行为频数的百分比。肉鸡出现该行为时间百分比为该休息行为发生时间占总休息行为发生时间的百分比[1]。

1.1.3Moment估计[18]

(7)

式中，

(8)

用Moment估计量表示的极值分位数为[17-18]

(9)

Moment估计量比Hill估计量的适用范围更广，但其估计方差更大，且仅在Pareto分布下渐近无偏[20]。

1.2　Sum-plot法

刘维奇等[21]的应用实例表明，Sousa[8]提出的Sum-plot法精度高于Bootstrap法和M-Bootstrap法。因此，本文选用Sum-plot法确定阈值k。

Sum-plot法是通过绘制{(k,Sk),1≤k≤n}曲线并观察其在哪一点偏离直线，从而认为该点对应的k值最优。

(10)

式中，X1,n≥X2,n≥…≥Xk+1,n为次序统计量。最优k值对应的图形直线部分斜率即极值指数γ。

2应用实例

2.1　分布判别

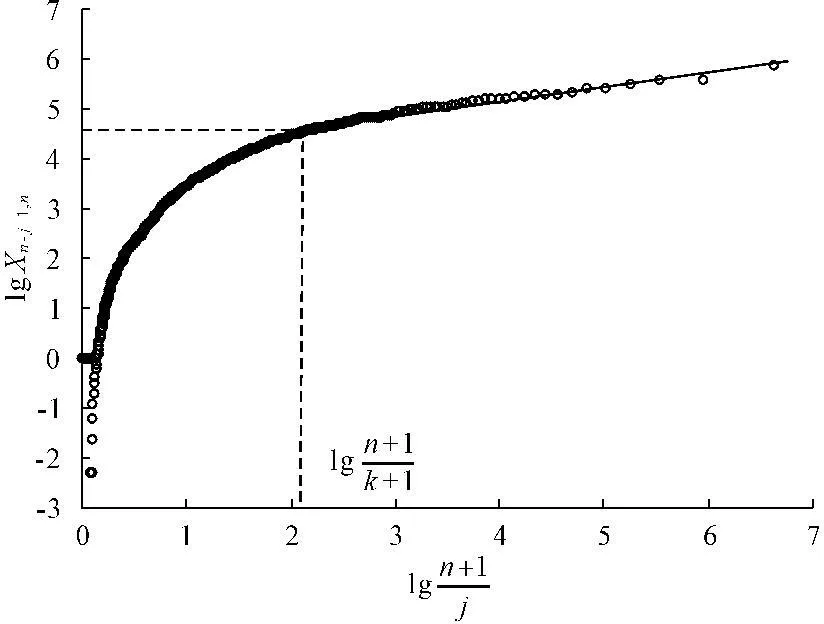
图1为太原站月降水序列的Pareto分位数图，其右上角部分近似线性，可认为该序列服从重尾分布，满足进行极值指数估计的前提条件。

2.2　不同估计量的性质及阈值k的确定

分别用Hill估计量、Pickands估计量及Moment估计量计算太原站月降水序列的γ并绘制γ-k曲线(图2)。由图2可知：γHill-k曲线随k值增大呈缓慢上升趋势；γPickands-k曲线随k值增大先波动后上升；γMoment-k曲线则能呈现平稳状态。理论上，γ-k曲线趋于稳定的一点即为阈值k的位置，但仅靠观察无法准确判断该点位置，主观任意性较大，故通过绘制Sum-plot图(图3(a))辅助判别。由图3(a)可知，随着k值的增大，Sum-plot图形由直线渐变为曲线。选取线性部分的Sk进行二次作图(图3(b))，根据(k,Sk)曲线偏离直线的点的位置确定最优k值，并注于图中。

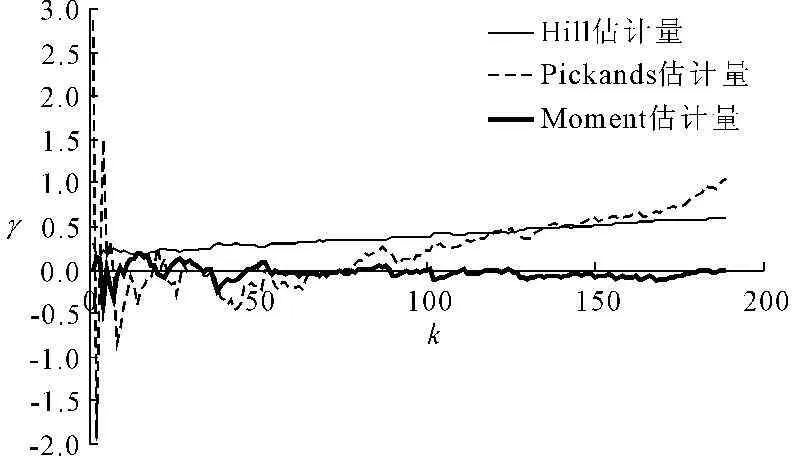
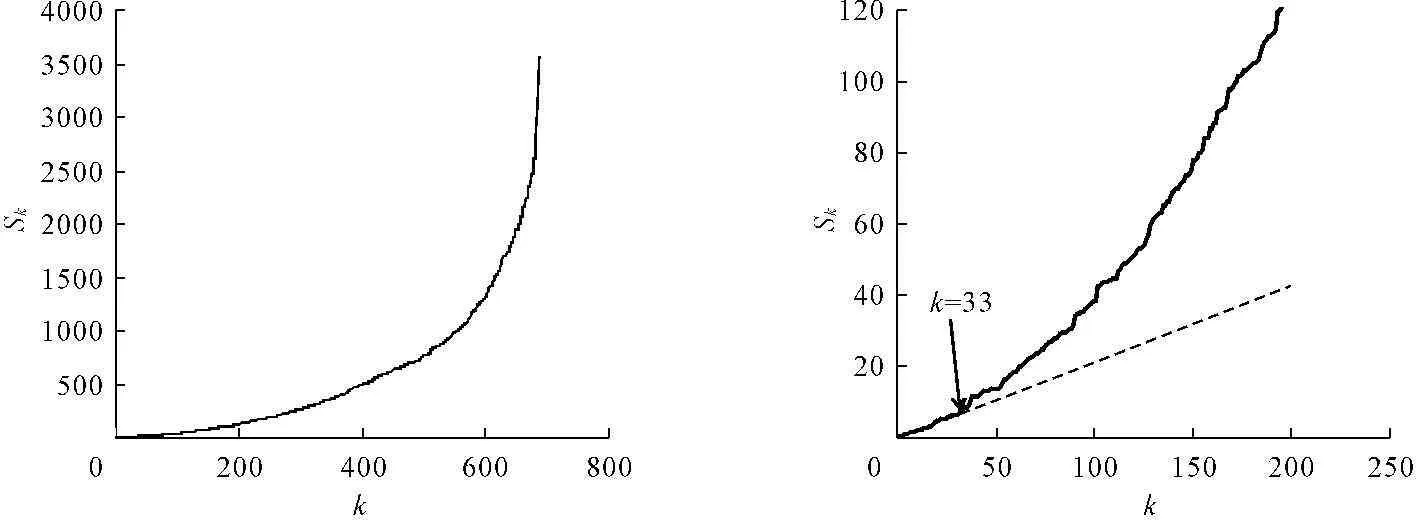
图2　太原站月降水序列γ-k曲线

图3太原站月降水序列Sum-plot图

2.3　极值指数估计

用选定的k值分别估计γHill、γPickands、γMoment，结果如表1所示。

表1　太原站极值指数估计量

由表1可以看出，三种估计量的值与正态分布(γ=0)相比均存在不同程度的差别：γHill的估计值显著偏大，γPickands和γMoment的估计值较为接近。根据引言中关于重尾分布的描述，可以认为太原站的月降水序列服从重尾分布，与2.1所得结论一致。

2.4　极值分位数计算及强降水拟合

给定不同的频率，将γ的估计值分别代入式(4)、式(6)、式(9)，即可计算出指定频率下的设计值。根据极值理论对极值事件风险的度量特性，本文对降水序列概率分布的研究重点集中在其尾部，即概率小、降水强度大时设计值与实测值的拟合情况。故选取太原站月降水序列中概率<25%的一段，观察强降水部分的拟合效果。

分别采用Hill估计量、Pickands估计量、Moment估计量计算太原站月降水序列的理论频率，并绘制理论频率曲线与经验点据拟合图，如图4所示。

图4太原站月降水序列理论频率曲线

比较不同γ估计量计算出的理论频率曲线对经验点据的拟合情况可知：当频率介于25%和5%之间时，Pickands估计量对应的理论频率曲线对经验点据的拟合效果最为理想，Moment估计次之，Hill估计相对最不理想；当频率<5%时，Moment估计量所得理论频率曲线对样本序列的较大值拟合十分理想，经验点据几乎全部落在理论曲线上，显著优于Hill估计量和Pickands估计量。根据极值理论的观点，可认为在给定频率接近0时，采用Moment估计量计算出的理论频率曲线对经验点据的描述最为确切。因此，Moment估计量是估计太原站极值指数及计算小概率设计值的理想估计量，可用于当地强降水事件的频率分析。

3结论

本文在介绍极值指数估计理论的基础上，以山西省太原站的月降水序列为例，用Pareto分位数图对其是否服从重尾分布进行了判别；选用3种常用极值指数估计量计算了序列的极值指数γ；为研究其尾部特性，选取序列中概率<25%的一段，观察并评价强降水部分的拟合效果。经分析计算得出结论：

(1) 太原站月降水序列服从重尾分布，极值指数γ可用于描述分布的尾部特性并进一步估算小概率强降水情况下的设计值。

(2) 采用Hill估计量、Pickands估计量和Moment估计量计算极值指数γ均较为简便。Sum-plot作图法确定阈值k的效果良好，精度较高，但该法需二次作图及观察，使得阈值选取存在一定主观性，在后续研究中仍需进一步探索更为精确的方法。

(3) 当频率介于25%和5%时，Pickands估计对月降水序列中强降水段的拟合效果最好，而Hill估计和Moment估计效果较差；当频率<5%时，Moment估计对强降水点据的拟合效果最佳。因此，可认为Moment估计量是太原站月降水序列极值指数及设计值计算的理想估计量，且计算简便、精度较高，可解决常用概率分布无法准确拟合强降水部分的难题，为当地月降水频率分析及强降水预测工作提供参考。

参考文献：

[1]丁裕国.气候概率分布理论的新内涵及其展望[J].沙漠与绿洲气象，2007，1(2):1-5.

[2]邹波.强降水发生的概率估计与比较[J].气候与环境研究，2003,8(3):331-337.

[3]Resnick S. Heavy tail modeling and teletraffic data[J]. Annals of Statistics, 1997,25(5):1805-1849.

[4]Drees H, De Haan L, Resnick S. How to make a Hill plot[J]. Annals of Statistics, 2000,28(1):254-274.

[5]Resnick S, Stǎricǎ C. Smoothing the Hill estimator[J]. Advances in Applied Probability, 1997,29(1):271-293.

[6]Kratz M, Resnick S I. The qq-estimator and heavy tails[J]. Stochastic Models, 1996,12(4):699-724.

[7]Trang Dang D, Sandor M, Vidacs A. Investigation of fractal properties in data traffic[J]. Journal on Communications, 1999,XLIX:12-18.

[8]Sousa B. A contribution to the estimation of the tail index of heavy-tailed distribution[D]. Michigan: The University of Michigan, 2002.

[9]Beirlant J, Bouquiaux C, Werker B J M. Semiparametric lower bounds for tail index estimation[J]. Journal of Statistical Planning and Inference, 2006,136(3):705-729.

[10]Hall P. Using the bootstrap to estimate mean square error and select smoothing parameters in nonparametric problems[J]. Journal of Multivariate Analysis, 1990,32(2):177-203.

[11]Danielsson J, De Haan L, Peng L, et al. Using a bootstrap method choose the sample fraction in tail index estimation[J]. Journal of Multivariate Analysis, 2001,76(2):226-248.

[12]刘维奇,赫英迪,邢红卫.选择重尾阈值K的Bootstrap方法[J].山西大学学报：自然科学版,2010,33(4):508-512.

[13]刘维奇,邢红卫.重尾指数估计中阈值K的简便优化估计[J].系统工程理论与实践,2010,30(8):1465-1470.

[14]李扬.水文频率新型计算理论与应用研究[D].杨凌：西北农林科技大学，2013.

[15]Hill B. A simple general approach to inference about the tail of a distribution[J]. Annals of Statistics, 1975,3(5):1163-1174.

[16]Pickands J. Statistical inference using extreme order statistics[J]. Annals of Statistics, 1975,3(1):119-131.

[17]Dekkers A L M, De Haan L. On the estimation of the extreme-value index and large quantile estimation[J]. Annals of Statistics, 1989,17(4):1795-1832.

[18]Dekkers A L M, Einmahl J H J, De Haan L. A moment estimator for the index of an extreme-value distribution[J]. Annals of Statistics, 1989,17(4):1833-1855.

[19]Drees H. Refined Pickands estimators of the extreme value index[J]. Annals of Statistics, 1995,23(6):2059-2080.

[20]刘维奇,邢红卫.重尾分布尾指数估计研究进展[J].山西大学学报：自然科学版,2012,35(2):163-173.

[21]刘维奇，赫英迪，陈琳.重尾分布的尾部指数估计及沪深股市实证分析[J].数学的实践与认识，2011，41(6):1-13.

[22]史道济,张春英.尾部指标估计中的阈值选择[J].天津理工大学学报，2006，22(6):78-81.

DOI:10.3969/j.issn.1672-1144.2015.04.011

收稿日期：2015-03-20修稿日期：2015-04-26

基金项目：国家自然科学基金项目(51479171，51179160)；高等学校博士学科点专项科研基金(20110204110017)

作者简介：李扬(1985—)，女，山西大同人，博士，工程师，主要从事水文学及水资源方面研究工作。E-mail：happyyang211@163.com

中图分类号：P333.1

文献标识码：A

文章编号：1672—1144(2015)04—0055—05

Research on the Application of Extreme Value Index Estimation in the Monthly Precipitation Frequency Analysis of Taiyuan Station

LI Yang

(ShanxiInstituteofWaterResourcesandHydropowerResearch,Taiyuan,Shanxi030002,China)

Abstract：This paper studied the extreme value index estimation methods and their application in monthly precipitation frequency analysis. Based on the introduction of extreme value theory and discrimination method of heavy-tailed distribution, three kinds of EVI estimators were selected. Monthly precipitation series of Taiyuan station in Shanxi province was chosen as an example for application of extreme value index estimation methods in monthly precipitation frequency analysis. The results showed that the distribution of monthly precipitation series of Taiyuan station was heavy-tailed distribution. Heavy precipitation section of series was best fitted by Moment estimator. Simple in calculation, high in accuracy, Moment estimator can provide reference for monthly precipitation frequency analysis in Taiyuan.

Keywords:extreme value index; monthly precipitation series; Hill estimator; Pickands estimator; Moment estimator