圆弧鼻坎射流水舌起挑角的试验研究

张晓艳，魏立婷，杨　慧，王　敏，任　宇

(1.山西大学 动力工程系， 山西 太原 030013； 2.河海大学 水利水电学院， 江苏 南京 210098)

圆弧鼻坎射流水舌起挑角的试验研究

张晓艳1,2，魏立婷1，杨慧1，王敏1，任宇1

(1.山西大学 动力工程系， 山西 太原 030013； 2.河海大学 水利水电学院， 江苏 南京 210098)

摘要：基于圆弧鼻坎挑射流物理模型试验，考虑脉动流速对水舌上缘挑角的影响，研究上缘起挑角的理论公式；通过引入两个系数同时考虑脉动流速和断面水深对下缘起挑角的影响，选用49组试验数据，采用误差分析方法，提出下缘挑角的半经验半理论公式。与前人的公式相比，上缘挑角的理论公式形式简单，下缘挑角公式考虑因素较多。两公式误差均小于13%，用于计算进口水平和倾斜渠道后接圆弧鼻坎挑射流水舌上、下缘起挑角是有效的，进而确定射流冲击点位置和冲击区范围也是有效的。

关键词：圆弧鼻坎；上缘挑角；下缘挑角；脉动流速

挑流消能工是在泄水建筑物的末端采用鼻坎将泄出的高速水流导向离建筑物较远的下游，使水流的能量在空中和下游水垫中消耗。这种消能工于19世纪30年代首次在法国使用，是一种比较经济、施工方便的消能方式，国内外已建坝高大于100 m的水电工程中绝大多数采用挑流消能[1]。当前，我国将在西南和西北地区陆续建设几十座高坝大型水电工程，这些工程具有高水头、大流量、深峡谷的特点，其泄洪功率最高可达105MW，这些工程的泄洪消能和下游冲刷防护问题十分突出，已成为工程中的关键技术问题[2-3]。为了保护高坝下游冲刷区，首先需要准确计算射流水舌上下缘挑距，确定冲击点位置和冲击区范围，从而预测冲刷危害和设计消力池。射流挑距的计算偏差直接影响到冲击位置，无法正确估算冲刷范围，甚至引起严重的冲刷危害，射流挑距的研究备受关注。如Steiner等[4]和张晓艳[5]研究了三角形鼻坎的水舌特性，张挺等[6]研究高扩散低收缩差动坎的射流水舌特性。

射流挑距是描述射流水舌的一个重要特性，射流挑距的估算是以射流轨迹为基础，描述射流轨迹的方程是以起挑流速(vo)和起挑角(α)为初始条件的刚体质点抛射体方程，针对射流挑距的估算方法，当前常见有四种研究手段：(1) Rouse[7]提出不考虑空气阻力对水舌运动的影响，假设起挑角α等于鼻坎挑角β的观点；(2) 针对具体工程的原型观测和模型试验研究；(3) 考虑空气对水舌运动的阻力作用，提出包含空气阻力影响系数K的抛射体方程[8-9]；(4) 考虑起挑角α不等于鼻坎挑角β[10-13]，水舌上下缘起挑角(αu，αl)不相等，分别计算水舌上下缘挑距(Lu，Ll)的方法[10-11]。

分析以上的四种观点，方法(1)形式简单，应用方便，大、中型水利工程《溢洪道设计规范》[14](SL 253-2000)推荐采用方法(1)对冲刷坑的位置进行初步估算。由于这种方法没有考虑空气阻力的影响，不适用于计算高速挑射流，特别是，当起始流速较大时，挑距计算结果与实测结果存在明显的偏差，且这种差别随起始流速的增大而增大[9]。方法(2)是针对具体工程的具体研究，这种方法充分考虑了实际工程中的各种影响因素，预测结果较准确，但不具备普遍性，其研究结果不适用于其他工程。方法(3)中，最具代表性的研究工作是刘宣烈[8]等提出K系数的理论表达式，理论式表明起挑角α是影响K系数的关键因素，然而方法(3)在计算挑距时依然假设起挑角α=β，没有考虑αu≠αl，也没有区分挑距Lu和Ll。方法(4)是以射流水舌起挑角α为主要研究对象，进而估算射流挑距，他们的研究成果仅考虑了圆弧鼻坎起始断面水深与反弧半径的比ho/Ro对于起挑角α的影响。

考虑到ho/Ro对于起挑角α的影响，谭新贤[12]和辛玉传[13]分别采用不同的方法得到相近的结论，即起挑角与鼻坎挑角的比α/β随相对水深ho/Ro增大而减小。最近，Heller等[10]和Pfister等[11]采用物理模型试验方法，分别研究了进口为水平渠道和倾斜渠道，出口为圆弧鼻坎挑射流水舌上下缘起挑角αu和αl，得到相似的结论，即挑角αu和αl均随ho/Ro的增大而减小，两种拟合公式均是ho/Ro的指数函数。

综上所述，过去的研究主要集中于水深和反弧半径之比对圆弧鼻坎射流水舌起挑角的影响，有的研究没有涉及下缘挑角[12-13]，有的结果没有考虑湍射流对起挑角的影响[10-11]，事实上，空气阻力以及射流的紊动、掺气和扩散等因素均对水舌运动产生影响，挑距的计算需考虑这些影响因素。由于高速射流最显著的特性就是紊动，脉动流速对起挑角的影响不可忽略[15-16]，水舌上缘主要受脉动流速的影响，而水舌下缘不仅受脉动流速的影响还受到水压力的作用，由此可知，下缘挑角小于上缘挑角，上缘挑角小于鼻坎出口边缘角。

本文目的是研究水舌上缘起挑角和下缘起挑角，分析脉动流速对于上缘起挑角的影响，提出上缘起挑角的理论公式；分析脉动流速和水深对于下缘起挑角的影响，通过理论分析和物理模型试验，提出下缘起挑角的半经验半理论公式，本文水深与反弧半径比的最小值为0.027。

1试验装置和试验程序

1.1　试验装置

试验是在河海大学高速水流实验室完成的。试验在某水电工程左岸1#泄洪洞1∶100模型(图1)上进行的，模型是按重力相似准则设计。整个试验系统包括：水泵和上游水库，泄洪洞和挑流鼻坎，下游河道，矩形薄壁量水堰和回水系统。水泵可为系统提供最大400 L/s的流量，上游水库水位调节范围为0 m～0.7 m；泄洪洞由短有压进水口、缓坡段和龙落尾共三段组成，总长21.70 m，进口与出口垂直高差1.2 m，缓坡段和龙落尾段为矩形明渠，其宽×高=0.15 m×0.065 m；圆弧形鼻坎安装于泄洪洞出口，作成可拆卸式，利于实现鼻坎体型变换；鼻坎尾部接下游河道，鼻坎进口底部与下游河道底部高差为0.65 m，有利于观察到足够长的射流轨迹。泄洪洞和鼻坎模型为有机玻璃。

图1圆弧鼻坎挑射流试验装置

图2为圆弧鼻坎挑射流流动示意图，圆弧鼻坎的体型参数包括反弧半径Ro，挑角β和挑坎高t，其中t=Ro(1-cosβ) ，在整个试验中鼻坎起始断面与下游河底高差w=0.65 m保持不变。描述上游来流的水力参数包括，射流起挑断面流速vo，起挑断面水深ho，起挑断面弗劳德数Fro=vo/(gho)1/2。鼻坎产生的射流可用上缘(u)下缘(l)轨迹描述，射流轨迹的起点位于鼻坎起挑断面边缘x=0，下缘起点在鼻坎顶部yu=0，上缘起点yl=ho/cosβ，上下缘起挑角分别为αu和αl，上下缘挑距分别为Lu，Ll。

图2挑射流流动示意图

1.2　试验程序

表1列出试验方案、鼻坎体型参数和挑射流水力参数。试验中考虑了三种反弧半径Ro=0.4 m，1.0 m和1.5 m，及三种鼻坎挑角β=15°、25°和35°。进口水深ho的变化范围为0.040 m～0.061 m，相对水深ho/Ro的变化范围为0.027～0.145，弗劳德数Fro变化范围为4.45～5.91。通过系统改变体型参数和水力参数，本研究共进行了25次试验，在表1中，分别用MA-ij和MB-ij表示两个系列的试验方案：(1)MA-ij系列模型中反弧半径Ro=1 m不变，挑角和水深变化，其中i=1，2，3，分别表示挑角β=15°、25°和35°；j=1，2，3，4，5，分别表示不同水深。(2)MB-ij系列模型中挑角β=25°不变，反弧半径和水深变化，其中i=1，2，3，分别表示反弧半径Ro=0.4 m、1.0 m和1.5 m；j=1，2，3，4,5，分别表示不同水深。

(2)

试验中用直尺测量进口水深ho，和上、下缘挑距Lu和Ll，误差为±1 mm；用矩形薄壁堰测量模型流量Q，精度为±1%。

2射流起挑角

2.1　理论分析

依据图2的直角坐标系，按照刚体质点抛射理论，挑射流水舌上、下缘轨迹线方程表示为：

(1)

挑距为：

式中：L为射流挑距。

由公式(1)导出射流水舌起挑角：

(3)

将x=Lu，y=-(t+w)，y0=ho/cosβ代入式(3)得到上缘挑角αu:

(4)

将x=Ll，y=-(t+w)，y0=0代入式(3)得到下缘挑角αl:

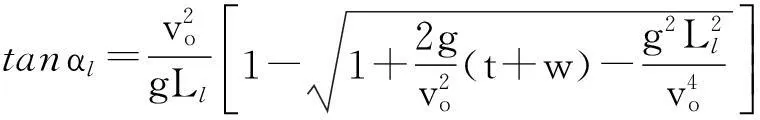
(5)

高速水流离开鼻坎挑入空气时，水舌脱离了鼻坎边界的约束，鼻坎底板对水舌顶托作用消失，水舌离开鼻坎的实际挑角α不等于鼻坎挑角β。水舌上缘在惯性力和水流脉动作用影响下，上缘起挑角αu小于鼻坎挑角β；水舌下缘在重力和惯性力，以及水流脉动作用共同影响下，下缘挑角αl小于上缘挑角αu。如果忽略射流起挑角α和鼻坎挑角β的差别，在公式(2)中直接采用鼻坎挑角β计算挑距，结果是不合理的，计算值通常大于实测值。正如前文分析，水舌起挑角小于鼻坎挑角，水舌下缘起挑角小于上缘起挑角，三种角度的大小关系为β>αu>αl，为了合理预测上下缘挑距，首先需要确定上下缘起挑角。

2.2　上缘起挑角αu

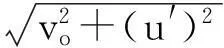
(6)

-18°≤β-φ≤40°,3≤Fro≤10

式中：φ是挑坎上游渠道与水平方向的夹角(水平渠道φ=0)，式中横向脉动流速u′的表达式为[11-12]:

(7)

式中：n为鼻坎边墙糙率，本文试验采用有机玻璃，n=0.01；r为水力半径，对于本文研究的矩形明渠，r=ho/(1+2ho/b)，其中b为渠道宽度等于0.15m。

2.3　下缘起挑角αl

与上缘不同的是，水舌下缘除了受到重力和惯性力的作用外，还受到水压力的作用，使得下缘起挑角αl，小于水舌上缘起挑角αu，这种差别随起挑水深ho的增加而增大。考虑到水舌上、下缘起挑角的差别(αu-αl)主要受到起挑水深ho的影响，不妨设：

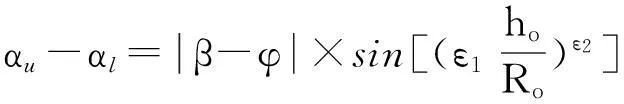
(8)

式中：ε1和ε2为待定系数。

用式(6)代替式(8)中的αu，得到下缘起挑角αl的表达式

αl=(β-φ)-arctan(u′/vo)×180°/π-

(9)

式(9)同时考虑了脉动流速和起挑水深对水舌下缘起挑角的影响，下面根据试验数据确定系数ε1和ε2。

2.4　系数ε1和ε2

为了确定ε1和ε2的值，选用本文和文献[7-8]试验实测挑距，采用公式(5)计算下缘挑角αlc，与公式(9)计算得到的下缘起挑角αlj进行比较，计算相对误差

(10)

以相对误差绝对值的最小平均值作为目标函数，选择公式(9)中的最优系数从而得到最优的起挑角公式。

(11)

式中，n=49为试验资料的总样本数。

由于式(9)中包含两个未知参数，需要进行两次误差分析分别求得两个参数。先设ε2=1，进行第一次误差分析，式(9)变形为

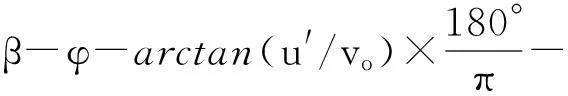
(12)

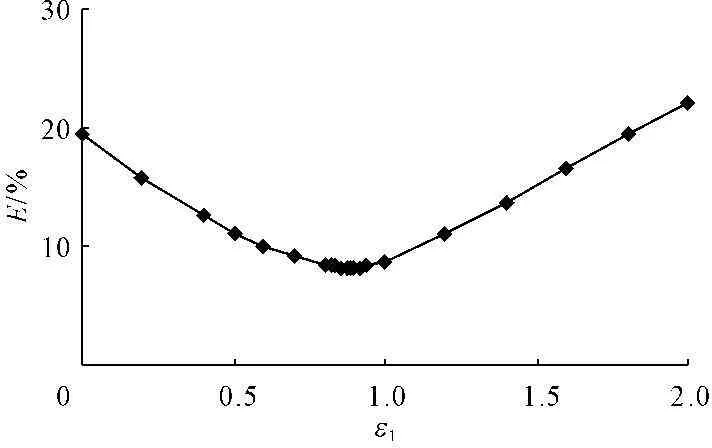
图3为αl的相对误差平均值随ε1的变化图，由图知当ε1=0.88，误差平均值最小为8.25%，将该结果代入公式(9)，进行第二次误差分析

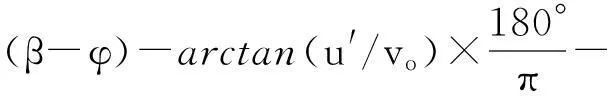
(13)

图3误差平均值随ε1的变化(ε2=1)

图4为αl的相对误差平均值随ε2的变化图，条件是ε1=0.88，由图4可知当ε2=0.98时，αl计算误差最小为8.21%。

图4误差平均值随ε2的变化(ε1=0.88)

为了进一步减小相对误差，同时对系数ε1和ε2进行小范围调整，调整得到最小误差为8.20%，最终确定系数分别为ε1=0.85，ε2=0.98，于是式(9)变为

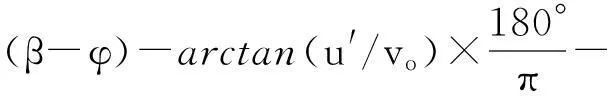
(14)

-18°≤β-φ≤40°，3≤Fro≤10，0.027≤ho/Ro≤0.34

3结果分析

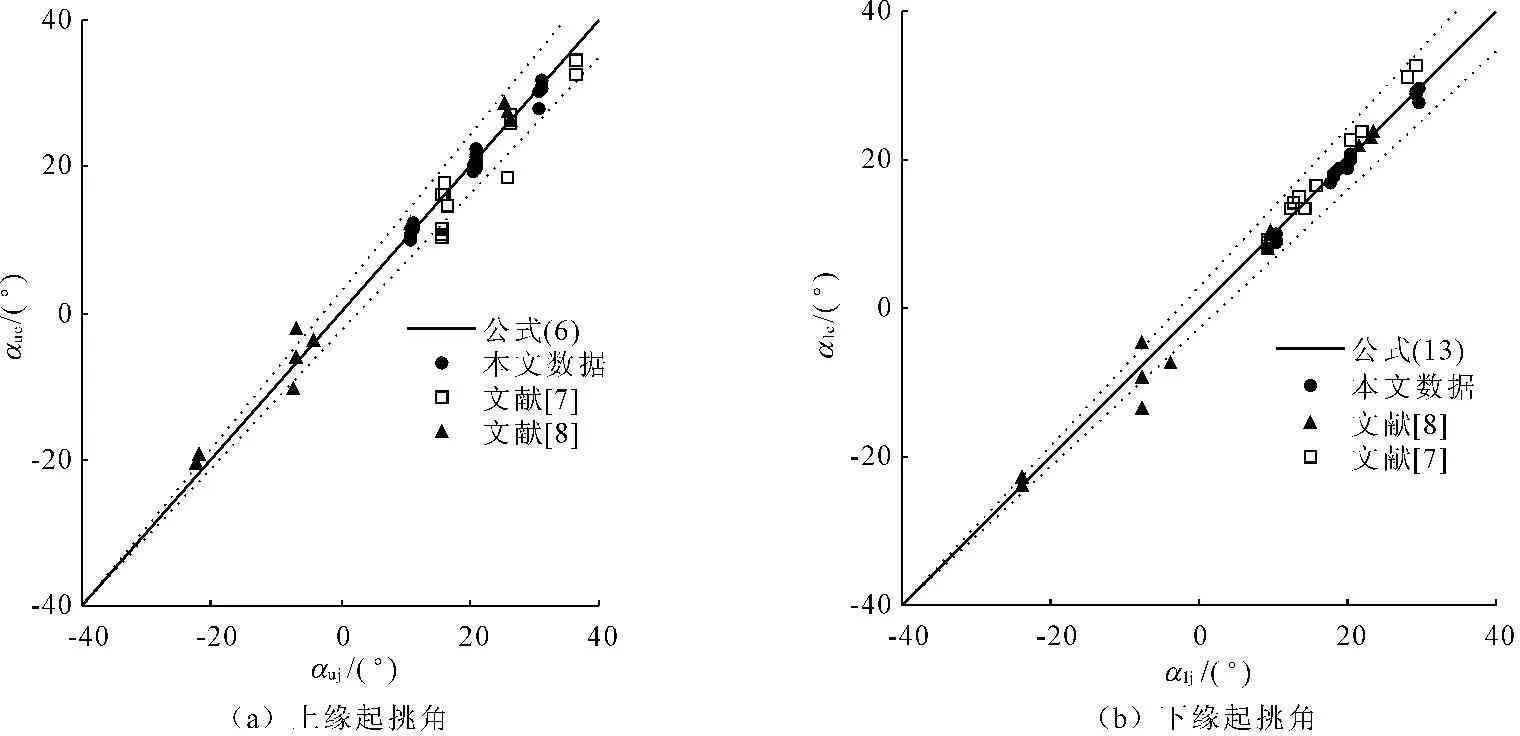
图5对比了本文计算结果和试验结果，其中图5(a)为上缘挑角试验值αuc与公式(6)计算值αuj比较；图5(b)为下缘挑角试验值αlc与公式(14)计算值αlj对比。图中的试验数据包括本文(实心圆点)，文献[7](空心正方形)和文献[8](实心三角形)试验值。图中的直线表示预测值与试验值完全相等，图中的虚线表示误差线，图5(a)和图5(b)中均为±13%。由图5可见，采用本文提出的理论公式(6)和半经验公式(14)分别计算圆弧鼻坎挑射流水舌上、下缘起挑角αu和αl的最大误差为±13%。公式对于渠道进口为水平和倾斜两种情况，在0.027

图5本文公式与测量值对比

由分析可知，本文提出的计算上缘挑角的理论公式和计算下缘挑角的半经验半理论公式都是有效的，本文提出的公式同时适用于进口水平和进口倾斜的渠道后接圆弧鼻坎，体型参数范围：12°<β<42°，-18°<β-φ<30°水力参数范围：0

4结论

考虑到挑射水流的紊动特性，本文研究脉动流速u′对射流水舌起挑角的影响，提出了上缘起挑角αu的理论公式；与试验值相与，最大误差为13%。基于理论分析和49组试验数据，采用误差分析方法，提出下缘起挑角αl的半经验半理论公式；与试验数据相比，相对误差平均值为8.20%，最大误差为13%。应用本文公式计算圆弧鼻坎挑射流起挑角，具有一定的精度。

参考文献：

[1]Ning Li Zhong. Discussion on the horizontal length of jet flow and its factors of influence[J]. Journal of Water Resources and water Engineering, 2004,15(3):35-39.

[2]Wu Jianhua, Yao Li, Ma Fei. Hydraulics of a multiple slit-type energy dissipater[J]. Journal of Hydrodynamics, 2014,26(1):86-93.

[3]Wu J H, Ai W Z, Zhou Q. Head loss coefficient of orifice plate energy dissipater[J]. Journal of Hydraulic Research, 2010,48(4):526-530.

[4]Steiner R, Heller V, Hager W H, et al. Deflector ski jump hydraulics[J]. Journal of Hydraulic Engineering, 2008,134(5):562-571.

[5]张晓艳.三角形鼻坎射流挑距综合影响系数的试验研究[J].山西大学学报：自然科学版,2015,38(2):263-269.

[6]张挺,陈虹,许唯临.高扩散低收缩差动挑坎II：收缩比对射流特性及冲坑的影响实验研究[J].水力发电学报,2013,32(5):140-146.

[7]RouseH.Dischargecharacteristicsofthefreeoverfall[J].CivilEngineering，1936,6(4):257-260.

[8]刘宣烈,张文周.空气对挑流水舌的影响[J].天津大学学报,1982(2):67-77.

[9]KawakamiKA.Studyofthecomputationofhorizontaldistanceofjetissuedfromski-jumpspillway[J].JapaneseSocietyofCivilEngineeringJournal,1973,219(11):37-44.

[10]HellerV,HagerWH,MinorHE.Skijumphydraulics[J].JournalofHydraulicEngineering, 2005,131(5):347-355.

[11]PfisterM,HagerWH,BoesRM.Trajectoriesandairflowfeaturesofskijump-generatedjets[J].JournalofHydraulicResearch, 2014,52(3):336-346.

[12]谭新贤.溢流坎挑流射程的简捷计算[C]//泄水建筑物消能防冲论文集，北京：水利出版社，1980.

[13]辛玉传.挑坎上的水流运动分析和挑距的简化计算[J].郑州工学院学报,1984(1):35-44.

[14]中华人民共和国水利部.SL253-2000溢洪道设计规范[S].北京：中国水利水电出版社，2000.

[15]GlazovAI.Calculationoftheair-capturingabilityofaflowbehindanaeratorledge[J].HydrotechnicalConstruction, 1985,18(11):554-558.

[16]WuJianhua,RuanShiping.Emergenceangleofflowoveranaerator[J].Journalofhydrodynamics,Ser.B, 2007,19(7):601-606.

DOI:10.3969/j.issn.1672-1144.2015.04.010

收稿日期：2015-04-03修稿日期：2015-05-11

基金项目：国家自然科学基金青年科学基金(51409187)；中央高校基本科研业务费项目(2014B03114)；山西大学本科生科研训练计划资助项目(2015013323)

作者简介：张晓艳(1970—)，女，山西榆社人，博士研究生，讲师，研究方向为水力学及河流动力学。E-mail: 1015858702@qq.com

中图分类号：TV653

文献标识码：A

文章编号：1672—1144(2015)04—0050—05

Experimental Investigation of the Takeoff Angle of Free Jet from the Circular-shaped Flip Bucket

ZHANG Xiaoyan1,2, WEI Liting1, YANG Hui1, WANG Min1, REN Yu1

(1.DepartmentofPowerEngineering,ShanxiUniversity,Taiyuan,Shanxi030013,China;2.CollegeofWaterConservancyandHydropowerEngineering,HohaiUniversity,Nanjing,Jiangsu210098,China)

Abstract：Free jet is considered a major element in the design of flood discharging and energy dissipation installations of high dams. The hydraulic characteristics of the jet that jumps through a flip bucket is an important research subject in the dissipation design. Based on the physical model test, the theoretical equation of the upper takeoff angle was discussed considering the influence of the fluctuating velocity, and then the lower takeoff angle was analyzed through two introduced parameters considering the fluctuating velocity and flow depth of the cross section. In the study of the lower takeoff angle, 49 units of test data were analyzed with error analysis method, and then a semi-empirical and semi-theoretical equation of the lower takeoff angle was put forward. The formula of upper takeoff angle has a simple form and that of the lower angle includes more affecting factors comparing to previous expressions. The formulas have the errors smaller than 13%, so they are applicable in the calculation of the takeoff angles of free jet from a flip bucket inserted at the end of the outlet, for both the horizontal and the inclined channels, based on which the location of the plunging point and the scope of plunging zones can be determined.

Keywords:circular-shaped flip bucket; the upper takeoff angle; the lower takeoff angle; the fluctuating velocity