鱼雷锚贯入土体过程数值分析

张金利，郝佳伟

(大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116023)

鱼雷锚贯入土体过程数值分析

张金利，郝佳伟

(大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116023)

摘要：鱼雷锚主要应用于采用紧绷式锚泊系统的浮动式采油平台中。采用LS-DYNA软件针对质量为40 t的鱼雷锚以一定冲击速度贯入海床土体的过程进行了数值分析。主要考虑鱼雷锚长径比(L/D)、冲击速度、海床土体的c、φ等参数变化对鱼雷锚贯入过程影响。计算结果表明，鱼雷锚贯入海床土体的过程为快速过程，总历时极短(秒级)，贯入过程可分为加速与减速两个阶段，其中减速阶段历时较长。贯入阻力随贯入深度增加而增大至峰值，当速度接近零时，贯入阻力出现陡降，最终贯入阻力(静阻力)与鱼雷锚重力平衡。随着冲击速度增加，贯入深度相应增大，且两者具有较好的线性关系。当冲击速度不变时，贯入深度随L/D增加而增大。海床土体强度参数c、φ的变化对鱼雷锚的贯入过程具有重要影响，随强度参数增加，贯入深度相应减小。

关键词：鱼雷锚；长径比；冲击速度；贯入深度；强度参数

开采海洋油气资源一般采用固定式或浮动式采油平台。因此，有效固定采油平台成为海洋油气开采工作中的关键问题。对于浅海环境，可通过安装在海床上的张力腿、桩、吸力式沉箱、拖锚等方式固定采油平台。在深海环境下，目前常采用平板锚、吸力式沉箱、拖锚等固定采油平台。由于水深大、海洋环境复杂，各种锚固设施的安装不仅极其困难，而且成本昂贵。近年来，在深海石油开采中，采用由锚与锚链组成的紧绷式锚泊系统固定采油平台。该锚泊系统中的锚型为拖锚或鱼雷锚。与拖锚相比，鱼雷锚安装主要靠重力自行贯入到海床中，不需要专业安装船舶，安装便捷且费用较低[1]。同时，在制作鱼雷锚时，可在其中充填废钢铁或混凝土，造价低[2]。

鱼雷锚所能提供的承载力受海床土体性质、贯入深度、长径比等共同影响。因此，研究不同长径比下的鱼雷锚贯入深度对于锚-锚链组成的锚泊系统的可靠性具有重要的理论与实践价值。William(1957)[3]试验研究弹头为锥形的子弹在砂中运动特性，并建立新的贯入方程。Boguslavskii(1996)等[4]通过试验与分析建立了锥形杆头长杆在砂中贯入的理论分析模型。True[5]通过小比尺模型试验，研究了不同锚头类型的鱼雷锚在软黏土、不同硬度水泥土中的贯入特性，基于承载力理论建立冲击速度与贯入深度的关系。为探索深海深埋核废料，Freeman与Burdett[6]在太平洋针对不同长径比，不同质量，不同锥角的8种鱼雷锚试验研究其贯入特性，获得了鱼雷锚的极限速度、贯入深度、贯入阻力等。Medeiros首次在巴西的Campos Basin进行鱼雷锚现场贯入试验[7]，实测了鱼雷锚最终贯入深度及承载力，但是并未对影响贯入深度和承载力的因素进行分析。Sagrilo等[8]对巴西国家石油公司的试验结果以及相应的数值分析结果进行统计模型的不确定评估，提出一种可靠性安全系数来改善鱼雷锚的设计。Carter等[9-10]采用ALE算法对长杆自由下落贯入试验进行分析，计算结果表明，ALE算法所得到结果与试验结果吻合较好。Mohammad[11]将海床土体假设为黏性流体下，采用计算流体动力学程序计算了鱼雷锚不同冲击速度与贯入深度的关系。O'Loughlin等[12-13]、Richardson等[14]分别针对鱼雷锚的贯入过程及后期承载力进行了离心机模型试验，较为完善的分析了影响鱼雷锚贯入过程及后期承载力的诸多因素。Hossain等[15-16]分别运用离心机模型试验及基于ABAQUS/Explicit的CEL算法对鱼雷锚贯入黏土及石灰质淤泥土的动态安装过程及单调荷载下的承载力进行了初步分析，证明了其试验和数值方法的可行性。

综上所述，早期对鱼雷锚贯入的研究主要为理论分析、现场试验、离心机模型试验。近年来计算机数值方法被运用到这一领域中，虽然开发了很多解决贯入过程大变形问题的数值方法，却没有对影响整个贯入过程的诸多因素进行系统的分析。本文基于LS-DYNA软件，针对可能用于工程的鱼雷锚，初步探讨了长径比、海床土体、冲击速度等因素变化下，对贯入深度、贯入阻力、加速度分布等影响。

1数值计算模型建立模型

1.1　运动方程[17]

计算域土体经离散后，各节点的动力平衡方程可表示为：

{Fi}+{Fd}+{p(t)}={Fe}

(1)

式中：{Fi}、{Fd}、{p(t)}分别为惯性力、阻尼力、动荷载；{Fe}为弹性力。

弹性力可用节点位移{δ}与刚度矩阵[K]表示为

{Fe}=[K]{δ}

(2)

(3)

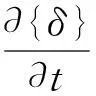
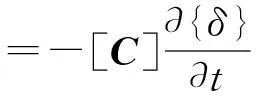
(4)

将式(2)～式(4)代入式(1)，得到运动方程为

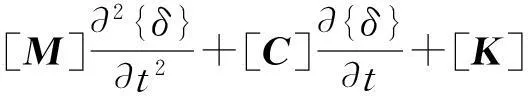
(5)

1.2　土体本构模型[18]

土体模型采用Soil-and-Foam-Failure模型，该模型可以模拟土体的大变形、失效等行为，在较低的屈服强度下，该模型表现出类似流体的行为。

图1为该模型的压力-体应变关系，V和V0分别为计算单元当前和初始的体积。当体积应变较小时，表现出弹性本构关系，超过弹性应变后，开始发生塑性应变，塑性应变累计到一定程度之后，土体的体积模量开始增大，表现为强化特性。

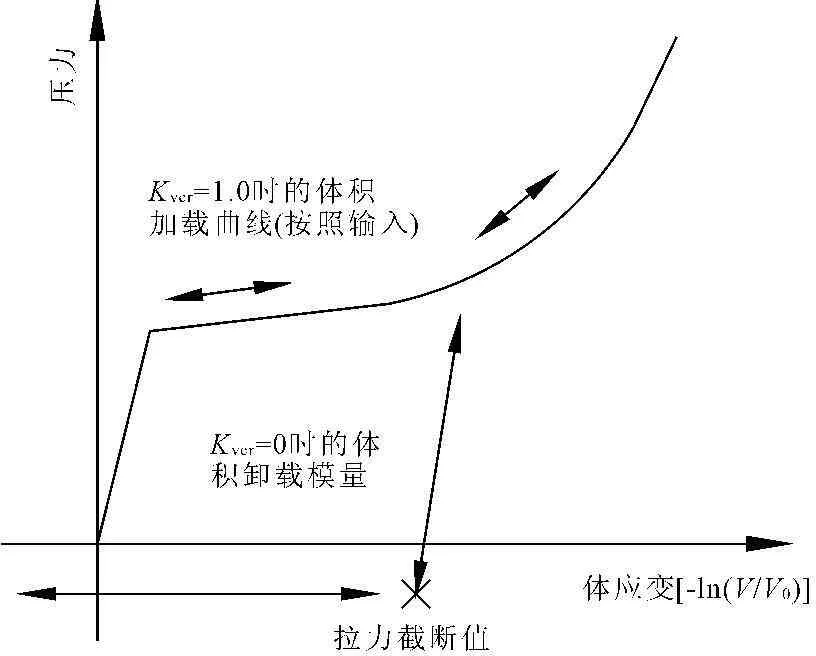
图1土及可压碎材料的压力-体应变关系曲线

在模型参数设置中，当参数Kvcr=1时，计算体积应变时的加载和卸载路径是相同的，因此在静水压力作用下，模型不会发生塑性变形；当参数Kvcr=0时，卸载计算时采用的体积应变按照指定的体积应变计算，模型可以模拟在静水压力作用时发生的塑形变形。由于在考虑静水压力的非线性行为时，模型是通过计算控制，而不是通过屈服准则来进行控制，实际计算中的矩阵采用的是弹性矩阵计算，并非弹塑性矩阵，因此该模型无法考虑土体的剪胀变形。

1.3　屈服函数

Soil-and-Foam-Failure模型采用的屈服函数可表示为

φ=J2-[a0+a1p+a2p2]

(6)

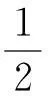
通过控制a0，a1，a2的取值，可实现Von Mises、Durcker-Prager、Mohr-Coulomb等屈服准则。

这里采用Durcker-Prager屈服准则，可表示为

(7)

式中：α、k是由试验确定的常数；I1为与静水压力相关的系数。令式(6)与式(7)相等，式(6)所代表的屈服函数即为Durcker-Prager屈服准则，则

a0=k2,a1=6αk,a2=9α2

(8)

式中：φ为土的内摩擦角；c为土的黏聚力。

1.4　鱼雷锚

假设鱼雷锚为刚体,采用MAT-RIGID模型，该模型内部所有节点的自由度都耦合到其质量中心，无论划分多少节点，鱼雷锚只有6个自由度，这样可以使计算效率显著提高。刚体材料在数值计算过程中是不变形的，但需要定义真实的密度、弹性模量和泊松比，因为处理锚和土之间的接触过程是需要计算接触表面刚度的。鱼雷锚在自由下落过程中仅发生竖向位移。鱼雷锚由锚头与锚杆组成，如图2所示。锚头为椭圆形，在质量(均为40t)相同下，具有不同长径比，具体参数见表1。

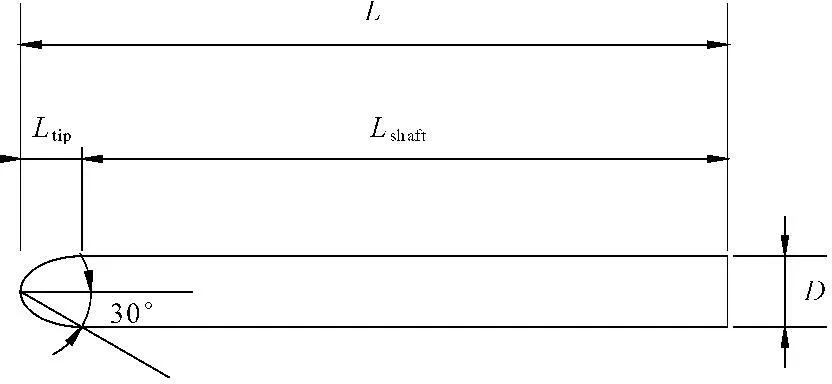
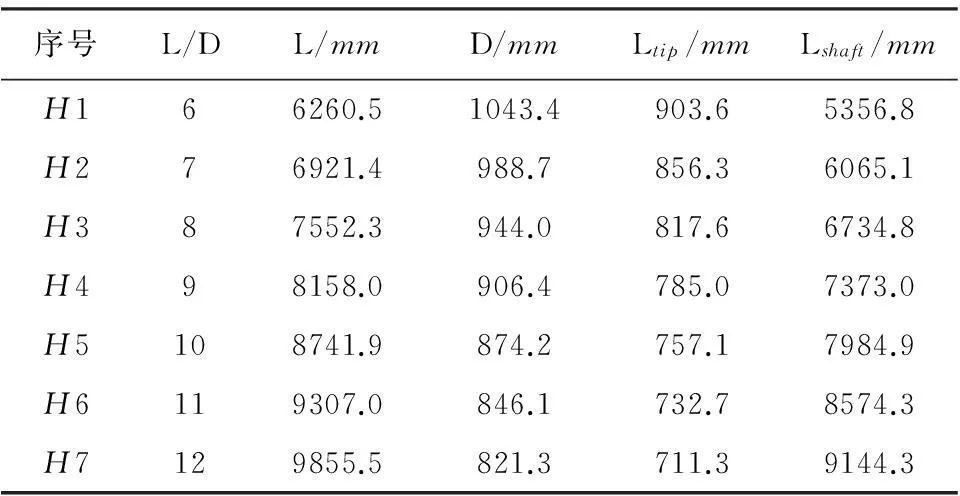
图2　鱼雷锚示意图

1.5　计算模型

鱼雷锚贯入海床土体具有轴对称性，为减小计算量，取1/4空间建模。土体水平向取8D(D为鱼雷锚直径)，竖向取4L(L为鱼雷锚长度)。鱼雷锚与土体均采用Solid164八节点六面体单元进行剖分。鱼雷锚锚头在径向、切向及轴向均8等分，锚杆在径向和切向8等分，轴向为9L/D-8等分。海床土在径向上，距中心轴0～2D为16等分、2D～4D为8等分、4D～8D为8等分，在切向16等分、轴向16L/D等分。总单元数为123424个，节点数为136 176个，详见图3。以上网格剖分针对L/D=12情况，其他情况类似。在鱼雷锚与土体的两个对称面边界上分别约束其法向位移，土体的外侧边界及底部边界约束全部为自由度。模型整体施加重力。

图3计算模型与网格剖分

1.6　计算参数选取

鱼雷锚的密度为7 850kg/m3，弹性模量为210GPa，泊松比为0.29。海床土体密度为1 880kg/m3，弹性模量为79MPa，泊松比为0.3，剪切模量为51.4GPa，卸载的体积模量K=24GPa。为探讨海床土体的变化对鱼雷锚贯入过程影响，分别取黏聚力(10kPa、20kPa、30kPa、40kPa)与内摩擦角(16°、18°、20°、22°、24°)进行具体分析。屈服函数中参数可由式(8)计算得到。

2计算结果与分析

2.1　鱼雷锚运动特性分析

在鱼雷锚冲击速度为20m/s，海床土体的强度参数为c=20kPa，φ=18°，鱼雷锚的长径比L/D=12下，分析了鱼雷锚的不同时刻贯入过程。图4给出不同时刻时，土体中的VonMises应力分布。

由图4可见，鱼雷锚在贯入海床土体的过程中，土中应力变化较大区域为锚尖周围有限范围，最大应力位于锚尖前端。当锚尖处应力达到土的抗剪强度后，锚尖处的土体首先破坏，随着锚尖周围土体中的应力增加，土体逐渐破坏，由锚尖开始逐渐形成柱孔。

图4贯入过程中不同时刻鱼雷锚周围

土体VonMises应力等值云图

图5～图7分别给出鱼雷锚贯入过程中的速度、加速度、总阻力时程曲线及速度深度关系曲线。由图5可见，当鱼雷锚以20m/s冲击速度贯入海床时，在贯入的初始阶段(0～0.3s)，鱼雷锚速度反而高于初始速度，表明鱼雷锚在加速，此时外部阻力小于重力，由加速度曲线可见，此时的加速度为负(规定向下为负)。上述结果与True[5]的试验结果一致。当鱼雷锚达到最大速度后，开始减速，此时加速度为正，且加速度随之不断增加，最大加速度约为50m/s2。为分析鱼雷锚贯入过程中的阻力影响，图7为鱼雷锚贯入过程中的总阻力(端部与侧壁阻力)随时间变化曲线。由图7可见，在贯入过程中，总阻力逐渐增加至峰值，然后下降，总阻力与鱼雷锚自重平衡，贯入过程停止。总阻力变化与加速度变化相对应，表明贯入过程中总阻力在不断变化。

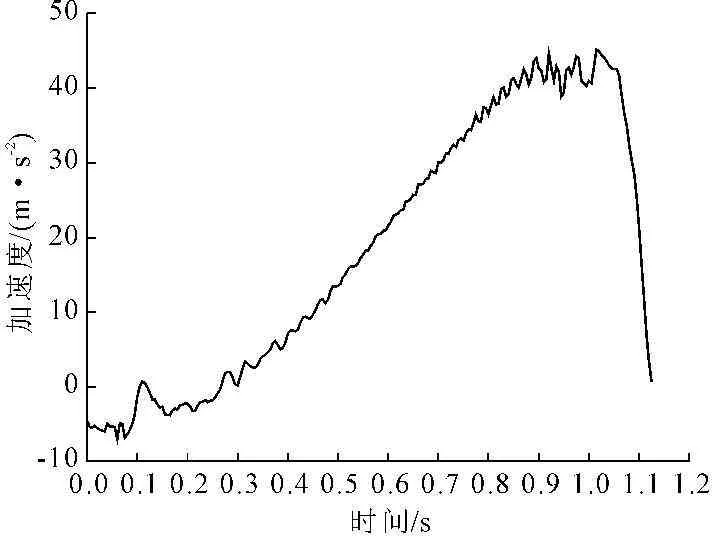
图5　鱼雷锚贯入过程中的运动速度随时间变化曲线(v0=20 m/s)

图6　鱼雷锚贯入过程中的加速度随时间变化曲线

由图8可见，当鱼雷锚以20m/s冲击速度贯入海床时，在贯入一定深度范围内(约为10m)，鱼雷锚速度处于增加阶段，当贯入一定深度后，速度迅速降低，直到停止，此时达到最大贯入深度。

图8鱼雷锚贯入过程中的运动速度随深度变化曲线

2.2　鱼雷锚冲击速度对贯入深度影响分析

为分析鱼雷锚的冲击速度对贯入深度影响，在海床土体的强度参数为c=20kPa，φ=18°，L/D=6、9、12情况下，变动鱼雷锚冲击速度v0=15m/s、20m/s、25m/s、30m/s，分析其对贯入深度的影响，计算结果如图9、图10所示。由图9可见，当L/D不变时，鱼雷锚贯入深度随冲击速度增加而增大，且随L/D增加而增大，当冲击速度较大时，其贯入速度降低较快。由图10可见，随冲击速度增加，贯入深度相应增大。

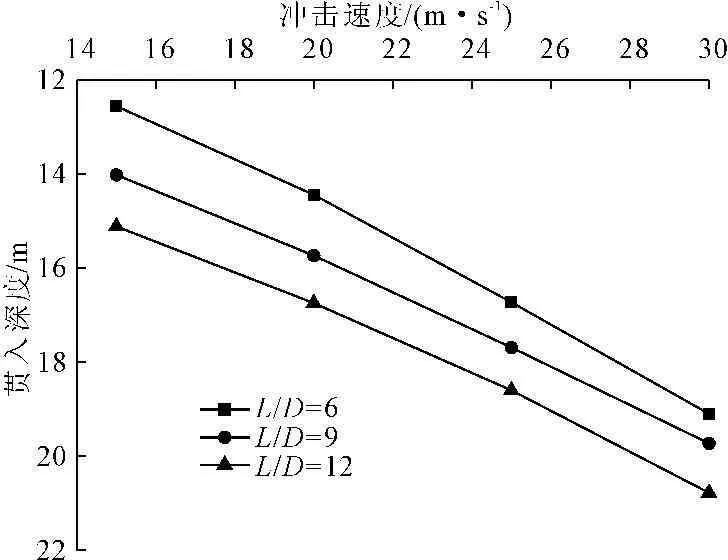
图9　鱼雷锚冲击速度对贯入深度影响

图10不同冲击速度下鱼雷锚运动速度随深度变化曲线

2.3　长径比与冲击速度变化对贯入深度影响分析

为研究鱼雷锚长径比与冲击速度变化对贯入过程的影响，取海床土黏聚力c=20kPa，内摩擦角φ=18°，在不同冲击速度(15m/s、20m/s、25m/s、30m/s)与长径比(L/D=6～12)情况下，较为详细地分析了鱼雷锚的贯入过程。计算结果如图11、图12所示。

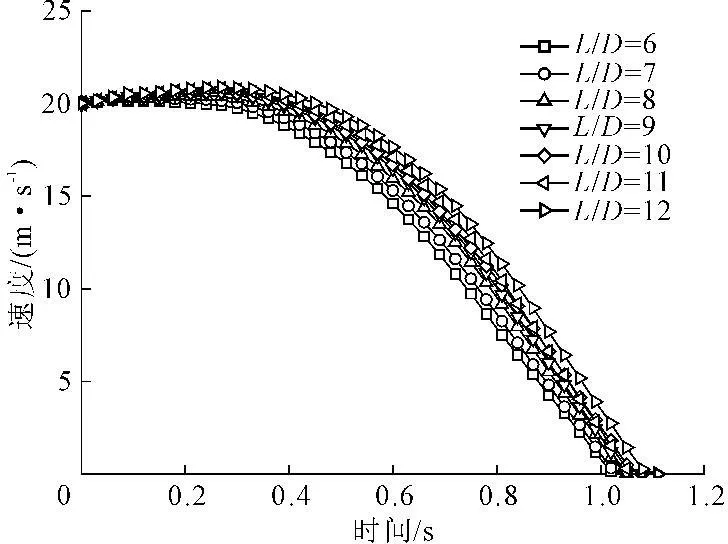
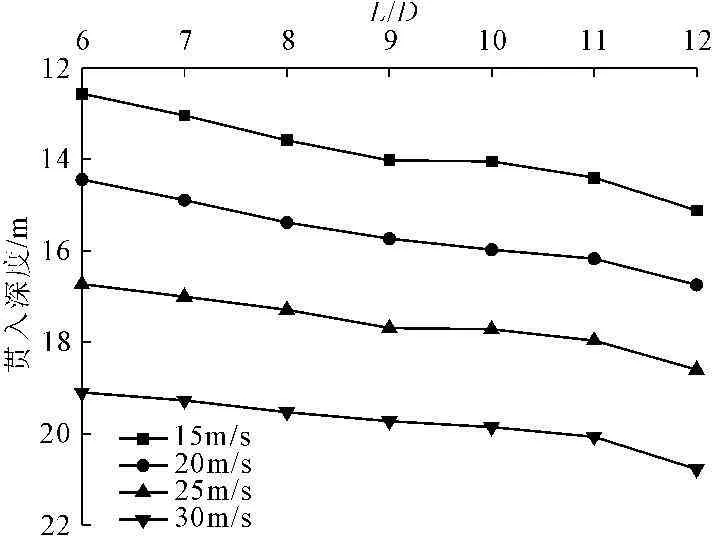
图11　鱼雷锚长径比对运动速度变化的影响(v0=20 m/s)

图12不同冲击速度情况下贯入深度和长径比的关系曲线

由图11可见，在鱼雷锚冲击速度相同下，鱼雷锚的长径比变化对贯入过程中的速度变化影响不大，长径比较大时，鱼雷锚贯入时间(停止)略有延长。由图12可见，当鱼雷锚的冲击速度相同时，贯入深度随L/D的增加而加大，且在L/D=6～9时，贯入深度与L/D具有线性关系，当L/D>9时，这种关系不再存在。产生上述结果的主要原因为，细长较短粗鱼雷锚的端部阻力小，在相同冲击速度下，可获得较大贯入深度。当冲击速度逐渐增加时，贯入深度随之增加。由此可见，对于特定海区海床土体，鱼雷锚贯入深度大小取决于冲击速度与长径比两者的组合，合理确定这种组合对于鱼雷锚设计至关重要。冲击速度较大时，贯入深度相应增加，而长径比对贯入深度影响小于冲击速度影响。

2.4　c变化对贯入的影响分析

在保持内摩擦角φ=18°、L/D=8、10、12，v0=20m/s下，变动黏聚力(10kPa、20kPa、30kPa、40kPa)，分析黏聚力c变化对鱼雷锚贯入速度与贯入深度的影响，计算结果如图13、图14所示。由图13可见，随c增加，鱼雷锚停止所需时间略有减小，表明c较大时，土体对鱼雷锚所产生的阻力相应较大，阻力所做功亦较大，在鱼雷锚初始动能相同下，其贯入深度必然下降(见图14)。由图14可见，当c固定时，贯入深度随L/D增加而增大，当L/D不变时，贯入深度随c增加而减小。由此可见，土体的强度参数c对鱼雷锚贯入过程具有重要影响，因此，在设计时，应充分了解海床土体的基本力学参数。

图13　c的变化对鱼雷锚运动速度影响(v0=20 m/s)

2.5　φ变化对贯入的影响分析

在v0=20m/s，c=10kPa，L/D=8、10、12情况下，变动φ(16°、18°、20°、22°、24°)，分析其对鱼雷锚贯入过程影响，计算结果如图15、图16所示。由图15可见，当冲击速度固定时，φ对贯入速度时程曲线影响与c相同，即随φ增加，贯入时间减小，相应贯入深度降低。由图16可见，当冲击速度与L/D不变时，贯入深度随φ增加而减小。当φ一定时，贯入深度随L/D增加而加大。由此可见，鱼雷锚的贯入深度为L/D与φ的函数。

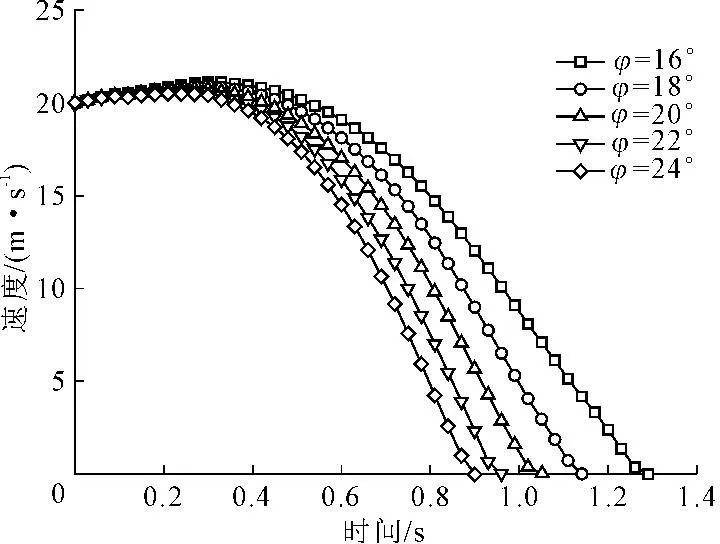
图15　φ的变化对鱼雷锚运动速度影响(v0=20 m/s)

图16φ与L/D的变化对贯入深度的影响(v0=20m/s)

3结论

基于LS-DYNA程序，针对重量为40t的鱼雷锚以一定的冲击速度贯入海床土体的过程进行了数值分析，主要分析了冲击速度、长径比、c、φ等参数变化对鱼雷锚贯入过程影响，通过对计算结果的综合分析，可得到以下结论：

(1) 鱼雷锚贯入海床土体的过程为快速过程，所需贯入时间均在秒级，该过程可分为加速与减速两个过程，加速阶段历时较短，减速阶段历时较长。

(2) 鱼雷锚贯入阻力随贯入时间增加而增大，直至峰值，当速度接近零时，阻力会出现陡降，最后达到稳定值，即鱼雷锚重量。鱼雷锚的贯入深度与冲击速度基本具有线性关系，即较大的冲击速度可获得较大的贯入深度。

(3) 在质量相同条件下，具有较大长径比的鱼雷锚可获得较大的贯入深度。随海床土体的强度参数c与φ的增加，鱼雷锚的贯入深度相应降低。

参考文献：

[1]FernandesAC,deAraujoJB,deAlmeidaJCL,etal.Torpedoanchorinstallationhydrodynamics[J].JournalofOffshoreMechanicsandArcticEngineering, 2006,128(4):286-293.

[2]MedeirosJrCJ.Lowcostanchorsystemforflexiblerisersindeepwaters[C]//OffshoreTechnologyConference, 2002.

[3]AllenWA,MayfieldEB,MorrisonHL.Dynamicsofaprojectilepenetratingsand[J].JournalofAppliedPhysics, 1957,28(3):370-376.

[4]BoguslavskiiY,DrabkinS,JuranI,etal.Theoryandpracticeofprojectile'spenetrationinsoils[J].JournalofGeotechnicalEngineering, 1996,122(10):806-812.

[5]TrueDG.Penetrationofprojectilesintoseafloorsoils[R].CivilEngineeringLAB(NAVY)PortHuenemeCA, 1975.

[6]FreemanTJ,BurdettJRF.Deepoceanmodelpenetratorexperiments[R].CommissionoftheEuropeanCommunities,Luxembourg, 1986.

[7]MedeirosJrCJ.Torpedoanchorfordeepwater[C]//ProceedingsoftheDeepOffshoreTechnologyConference(DOT’01). 2001.

[8]SagriloLVS,deSousaJRM,deLimaECP,etal.Reliability-BasedDesignofTorpedoAnchors[C]//ASME2010 29thInternationalConferenceonOcean,OffshoreandArcticEngineering.AmericanSocietyofMechanicalEngineers, 2010.

[9]CarterJP,NazemM,AireyDW,etal.Dynamicanalysisoffree-fallingpenetrometersinsoildeposits[C]//ProceedingsofGeoFlorida2010:advancesinanalysis,modelinganddesign,WestPalmBeach,Florida,USA, 20-24February2010.AmericanSocietyofCivilEngineers(ASCE), 2010.

[10]NazemM,CarterJP,AireyDW,etal.Dynamicanalysisofasmoothpenetrometerfree-fallingintouniformclay[J].Géotechnique, 2012,62(10):893-905.

[11]RaieMS,TassoulasJL.Installationoftorpedoanchors:numericalmodeling[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2009,135(12):1805-1813.

[12]O'LoughlinCD,RandolphMF,RichardsonM.Experimentalandtheoreticalstudiesofdeeppenetratinganchors[C]//OffshoreTechnologyConference.OffshoreTechnologyConference, 2004.

[13]O’LoughlinCD,RichardsonMD,RandolphMF.Centrifugetestsondynamicallyinstalledanchors[C]//ASME2009 28thInternationalConferenceonOcean,OffshoreandArcticEngineering.AmericanSocietyofMechanicalEngineers, 2009.

[14]RichardsonMD,O’LoughlinCD,RandolphMF,etal.Setupfollowinginstallationofdynamicanchorsinnormallyconsolidatedclay[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2009,135(4):487-496.

[15]HossainMS,KimY,WangD.PhysicalandNumericalModellingofInstallationandPull-outofDynamicallyPenetratingAnchorsinClayandSilt[C]//ASME2013 32ndInternationalConferenceonOcean,OffshoreandArcticEngineering.AmericanSocietyofMechanicalEngineers, 2013.

[16]KimY,HossainMS,WangD.NumericalModellingofDynamicInstallationofaTorpedoAnchorinCalcareousSilt[C]//TheTwenty-fourthInternationalOceanandPolarEngineeringConference.InternationalSocietyofOffshoreandPolarEngineers, 2014.

[17]PrakashS.Soildynamics[M].NewYork:McGraw-Hill, 1981.

[18]HallquistJO.LS-DYNAkeyworduser’smanual[M].LivermoreSoftwareTechnologyCorporation, 2007.

[19]陈万祥,郭志昆,袁正如,等.地震分析中的人工边界及其在LS-DYNA中的实现[J]. 岩石力学与工程学报,2009,28(增)：3504-3515.

DOI:10.3969/j.issn.1672-1144.2015.04.007

收稿日期：2015-03-03修稿日期：2015-04-19

基金项目：国家自然科学基金资助项目(51179023)

作者简介：张金利(1964—)，男，吉林辽源人，博士，副教授，主要从事环境岩土工程方面的教学与科研工作。E-mail:zhangjinli@sina.com

中图分类号：P751

文献标识码：A

文章编号：1672—1144(2015)04—0033—07

Numerical Analysis of Torpedo Anchor Penetration in Soil

ZHANG Jinli, HAO Jiawei

(StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian,Liaoning116023,China)

Abstract：Torpedo anchors are mainly used in taut-leg mooring system of floating production facilities. In order to understand the influence of torpedo anchor length to diameter ratio, impact velocity and the strength parameters of seabed soil on the penetration of torpedo anchor, this paper used the finite element analysis software LS-DYNA to study the process of 40t torpedo anchor penetration in seabed soil at a certain velocity. The numerical results indicate that it is a very fast (usually within seconds) penetration process, which can be divided into two phases, namely the acceleration phase and the deceleration phase, with the latter lasting longer. The resistance force increases with the depth of penetration until it peaks, while suddenly drops when the velocity is close to zero, and finally reaches torpedo anchor's gravity (static resistance force). The depth of penetration increases with impact velocity with good linear relation. When impact velocity is constant, the depth of penetration increases with the length to diameter ratio (L/D). The strength parameters c and φ have great influence on the penetration process, the depth of penetration decreases with the increase of these strength parameters.

Keywords:torpedo anchor; length to diameter ratio; impact velocity; depth of penetration; strength parameters