浅议物理实验测量误差和不确定度的异同

胡 勇，王严东

(1.中山福瑞特科技产业有限公司，广东 中山 528400;2.吉林化工学院，吉林 吉林 132022)

大学物理实验中实验结果不确定度的表示，对学生来说一直是个难点。工科学生一般很难搞清不确定度的具体含义，只能按照书上的基本计算公式来写出实验结果。一般工科院校在大学物理实验绪论课中要向学生讲清实验的数据处理以及误差和不确定度的表示方法［1］。所以对于误差和不确定度的表达方式是大学物理实验绪论课程中的重要组成部分。

由于误差表示比较直接，字面上的物理意义清晰，学生会直接将其理解为“测量值和真值的差”，误差概念和高中物理知识衔接紧密，学生接受起来容易。但误差的应用实际已经被淘汰，由于真值的不可测量误差实际不可能被测出，只能用多次测量的“约定真值”来计算误差，因此现在测量中一般都用不确定度来对测量结果进行表达。由于误差理论和不确定度存在着数学、物理理论上的多处联系，二者概念容易混淆，因此对测量误差和不确定度的区别和联系需要进行深入探讨［2］。

1 物理测量不确定度

物理量测量不确定度是对物理量测量结果可信程度的评估。不确定度是与测量结果关联的一个参数，用于表征合理赋予被测量的值的分散性。它可以用于“不确定度”方式，也可以是一个标准偏差(或其给定的倍数)或给定置信度区间的半宽度。该参量常由很多分量组成，它的表达(GUM)中定义了获得不确定度的不同方法［3］。

由于测量中存在人为因素、测量技术的理论缺陷以及仪器设备的不完善，对于直接测量的物理量不同次测量得到的结果是不一样的，而是以一定的概率分散在某个区域内的多值，也就是说我们无法通过测量而得到被测物理量的真值。客观存在的绝对误差是一个相对确定的值，但由于人们无法完全掌握它的真值，因此测量值只能认为它是以某种概率分布于一定区域内，并且这种概率分布本身也具有分散性。测量不确定度正是一个说明被测物理量之值分散性的重要参数，它反映了随机不确定度分量和未定系统不确定度分量的联合分布范围。测量不确定度可由传统误差理论求得，测量结果表述必须同时包含赋予被测量的值及与该值相关的测量不确定度。由于物理量测量结果的不确定涉及到仪器的准确性、测量方法的缺陷、测量时人为因素等多种原因，因此对于测量不确定度按是否用统计的方法求得，分为A类和B类两种。

A类不确定度是通过对多次测量结果进行分析，用概率统计的方法计算出的不确定度评定分量;B类不确定度是通过修正系统误差后列出测量值其他的的全部误差因素，依据经验或其它信息进行估计而求出的不确定度分量。A类和 B类分量最后用均方差的方法进行合成。由于标准偏差是描述多次测量平均值落在真值附近的概率，因此在大学物理实验中，一般把A类不确定度用多次测量(直接或间接)的标准偏差代替。对于B类不确定度需要靠经验和其他信息进行估算，学生一般无法单独给出。如:由于使用时间、设备磨损等原因导致同样一组多台设备测量精度并不相同，测量同一物理量其结果也不相同。这就要求实验指导教师具体向学生讲解，告知学生所用设备的情况，给出相应的B类不确定度。

2 测量误差

在物理实验中，待测物理量都是为客观存在，在具体固定的条件下(如固体密度在一定温度、压力条件下为定值)具有不以人的意志为转移的客观大小，人们将它称为该物理量的真值。物理实验对物理量进行具体测量是想要获得待测量的真值。然而测量要依据一定的基本理论，使用一定的仪器设备，在一定的外部环境中，由具体的实验人员人进行测量。由于物理理论上存在着一定近似性，方实验法上难以完善，实验设备灵敏度和分辨力有限，周围外界环境不稳定等因素的影响，待测量的真值是不可能被测得的，因此物理量的测量结果和被测量真值之间总会存在偏差，这个偏差叫做测量的误差［4-5］。

物理实验对于待测物理量的测量分为直接测量和间接测量两种。

直接测量是指可以用测量仪器和待测物理量进行直接比较得到的结果。例如用游标卡尺、天平、电压表和、弹簧秤等进行长度、质量、电压和力的测量就是直接测量。

间接测量则是不能直接用仪器把待测物理量测出来，而要依据待测量与某几个直接测量量的函数关系求出待测物理量。例如圆柱形固体密度，可通过天平测量固体的质量、游标卡尺测量圆柱高度、螺旋测微仪测量圆柱直径最后再由密度公式(1)

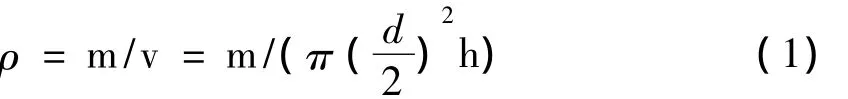
计算间接得出结果，这种类型的测量就是间接测量。

测量误差主要分为系统误差、偶然误差、过失(粗大)误差。

在完全相同的外界条件下，用同一台的实验设备对某量进行了多次观测，若误差出现的大小和符号均按一定的规律变化导致被测结果总向偏大或偏小的一方进行，这种测量误差被称为系统误差。系统误差的来源可以是测量理论别的不完善、外界原因等多种，一般在结果中予以修正。如热胀冷缩原因导致夏天的尺子比冬天长，导致室外测量长度时会使结果偏小;伏安法测电阻时表头内阻带来的误差会使结果整体偏大或偏小。

在相同的观测条件下，对某物理量进行了多次测量，由于测量的随机性导致误差出现的大小和符号均不一定，而是按照一定概率分布在一定区间，这种误差称为偶然误差。比如用分光仪的读数误差、天平多次的质量测量等都属于偶然误差。

偶然误差在观测前不能预知其出现的大小和方向，但若在固定的外界观测条件下，误差列却呈现出一定的统计规律性。随着观测次数的增大偶然误差的统计规律性会表现得更加明显，逐渐趋于高斯分布。对于偶然误差可以用数理统计方式进行估算，一般用多次测量的标准偏差进行表达。

在一定的测量条件下，由于人为操作失误而出现的不符合实际情况的误差称为粗大误差，如测量长度由于人为失误，读错标尺数值。对于粗大误差可以用统计的数学方法进行提剔除。

3 测量误差和测量不确定度异同

3.1 测量误差和不确定度的区别

从物理定义上测量不确定度表明被测物理量量值的分散性，表示由于测量的具体存在使得测量值不能确定的程度，按某一置信概率给出真值可能落入的区间。测量不确定度用标准偏差、标准差的倍数或给定概率下置信区间的半宽来表示，它不是具体的真误差，只是以参数形式定量表示无法修正的那部分误差范围。而误差在多数情况下是指测量误差，它的传统定义是测量结果与被测量真值之差，表明测量结果偏离真值的程度，它是一个确定的值。但由于物理量真值的不可知性，我们只能在特定的条件下寻求最佳的真值近似值，即所谓的约定真值来和测量值进行比较，给出测量误差。所以测量误差在定义上来说就是不可求的。

从来源分类上测量不确定度按是否用统计的方法求得分为A类和B类不确定度两种，合成方法为方均根。而测量误差通常是按出现于测量结果中的规律分为两类:系统误差和随机误差，没有提到其他来源而出现的误差。

测量不确定度可以根据实验数据、现象、资料和经验等信息进行评定，可以按理论定量估计测量不确定度的值;而误差由于测量真值的不可知性，用约定真值代替真值时，得到的仅仅是测量误差的估计值。

测量不确定度不能直接用于对测量结果进行修正，只能按置信程度给出测量结果落在真值附近一定范围的几率;对误差而言，当已知系统误差的来源，可以对测量结果直接进行相应修正。对于测量不确定度，当了解了测量数据的统计分布时，可按置信概率给出置信区间，对于误差，只有随机误差存在置信概率，最后结果很难用置信概率表示清楚。

3.2 不确定度理论和误差理论的关系及进展

测量不确定度与误差都是对测量过程不完善性的评定，都是物理量实际测量的理想概念。在估算测量不确定度时，用了一些描述误差分布的特征参量，一般也把A类不确定度就用偶然误差来代替，两者在分析方法、合成方式和数学传递公式上有很多相同之处。对于间接测量结果进行误差和不确定度的计算都要用相同的误差传递公式，两者之间在理论上有着相同之处。其次，实验结果标准差表示是成熟的数学统计理论，它是分析误差的基本手段，也是不确定度理论的数学基础，从本质上说不确定度理论是在误差理论上发展起来的，其基本分析和数学计算方法是共同的。

测量不确定度概念的提出避免了使用被测量理不可知的真值，它只与具体测量条件相关，较之测量误差更便于量化评定。但不确定度理论是大学课程内容，与高中物理教学脱节，会导致学生进入大学对其概念混淆，不鞥理解不确定度的物理图景。在传统误差理论中，随机误差与系统误差的分类不够严密，这两类误差分量往往没有截然的分界线，在一定条件下会相互转化，从而给数据的分析和处理表达带来困难。而测量不确定度表述的是可观测量的测量结果及其具体变化范围，因此用测量不确定度评价测量结果比用误差表达更加科学合理。测量不确定度概念的提出及其评价体系是对传统误差理论的基础理论修正，会使科学测量结果表达在定义上更加有着清晰的物理意义，是物理测量理论的一大进步。

［1］倪燕茹.基于测量不确定度评定的数据处理方法［J］.大学物理实验，2012，25(1):67-69.

［2］冯登勇，王昆林.声速测定实验不确定度、误差之比较研究［J］.大学物理实验，2014，27(1):88-91.

［3］刘敏，王严东.测量不确定度与误差的区别和联系［J］.吉林建筑工程学院学报，2009，26(2):94-96.

［4］方心，张瑞波.误差理论中几个问题的讨论［J］.大学物理实验，2011，24(3):86-89.

［5］张前勇，孙海燕.测量误差与测量不确定度表述方法的研究［J］.测绘工程2003，12(1):19-21 .