非恒定流理论在白龟山水库水面线计算中的应用

褚青来（河南省燕山水库管理局 郑州 450003）

非恒定流理论在白龟山水库水面线计算中的应用

褚青来
（河南省燕山水库管理局 郑州 450003）

水库（河道）在发生大洪水时，在上游一定形成水位壅高现象，势必造成水库末端水位高于坝前水位。针对此问题，利用水力学非恒定流理论，采用“瞬态差分法”，结合白龟山水库具体情况，选用合适的边界条件、初始条件和相关参数，对课题进行了分析计算，给出了数值结果，对水库防汛调度决策具有一定的参考意义。

非恒定流 水面线 差分法 边界条件 断面 流段

1 概况

白龟山水库水面顺水流方向成窄长形，左岸为山丘，右岸为副坝（即顺河坝），正常蓄水位水面面积约50km2，最宽6km，最窄为3km，库区106m高程平均宽度约4m，正常回水长度16.6km。

水库在顺河坝桩号13+500～14+500处设有爆破分洪段，根据调度规划，发生洪水时，当预报水库坝前水位达107.10m时，相机爆破分洪。当发生较大洪水时，入库流量过程一般较大，且洪峰来势较陡。根据水力学原理，在狭窄的库面上遭遇大的洪水，水库的水面线一定呈抬高之势，即上下游一定产生较大的水位差。而距主坝14km的分洪段，水位变化情况如何，应高出拦河坝水位多少，这一直是管理人员关心的问题，对此，笔者应用水力学理论对其进行了分析计算。

2 确定水面线计算方法及公式

水面线的计算方法有多种，每一种方法都有它适用的范围和条件。由于大洪水入库时，其流量是随时间变化的过程，且在洪峰附近量大峰陡，是典型的非恒定流的特征，采用非恒定流理论（以下简称非恒定流）较为合适。非恒定流方程式中含有时间和距离要素，因此计算出的水面线是动态的，即Z＝f（S，t），这与问题的特征相一致。如果用恒定流计算，水流不随时间变化，显然与实际不符，计算结果误差必然较大；用水量平衡法理论，因计算公式过于简化，水力要素偏少，计算结果近似估算，难以采信。

非恒定流理论的方程组是根据水流的连续性方程和能量方程推导而得，理论严谨，要素全面，是河道（渠道）水流计算的基本公式，恒定流、水量平衡等原理均是由此简化推导。由于天然河道或水库的断面形状极不规则，不可能由方程组直接积分求解，一般多利用计算机采用“瞬态差分法”、“库郎格式差分法”等求解，本文采用“瞬态差分法”。

根据差分法原理，在有限长的河道（或库区）中划分若干流段，认为每个流段的水力要素基本恒定或呈线性变化，这样就可将基本微分方程组转化为差分方程组，同时略去影响较小的局部水头损失，流速不均匀系数取1，差分方程组如下：

式中：Q-流量；Z-水位；A-过水断面面积；ΔS-上下游断面间距；Δt-时段长；K-流量模数；下标u、d代表上、下断面，上标'、"代表时段初、末，－代表均值。

方程组（1）是河道水流计算的基本方程式。

3“瞬态差分法”计算水库水面线方法步骤

用“瞬态差分法”计算需要确定各断面水力要素及第一边界条件、第二边界条件和初始条件，结合白龟山水库的实际情况，下面对各个问题逐个进行分析处理。

3.1 流段划分

将水库库区沿近似垂直原河槽的方向划分若干断面，各相邻两断面之间即为流段，为保证计算精度，各流段长度应适当。对断面资料的选取，采用水库淤积测量断面，这些断面的布设满足断面划分原则，同时对资料进行必要的甄别和技术处理，使断面形状尽量平顺，无尖角现象。为提高计算速度，并保证有一定的精度，从其中挑选14个断面，断面编号为 1、6、11、16、21、26、31、36、41、46、51、56、61、66，间距多在1000m左右。其中，1号断面的地理位置位于拦河坝坝脚，56号断面在分洪段处，66号断面为计算的入流断面。

3.2 流段水力要素

各流段断面的原始资料系采用原淤积测量成果，将其计算转换为各断面的水深～面积、水深～湿周关系。

3.3各流段糙率的确定

库区内地形比较复杂，既有河洼滩地又有为数较多的沙岛，在103.50m高程以上的滩地中有大片的高杆农作物、树林等阻水物，根据水力学中糙率值的确定原则并结合专家的经验，全库区糙率选用n＝0.07。

3.4 非恒定流初始条件及边界条件的确定

①初始条件：对于河道，其初始条件就是河道水体在做恒定流时各断面的水深，对于给定河段一般比较容易求得，对于水库，一般不易形成恒定流，只能假定。这次计算假设在大流量入库之前水库水体为恒定流运动，恒定流流量为闸门全开时相应库水位下的水库泄流量，据此时的坝前水位及流量可以算出库区沿程各断面的水位，计算公式采用恒定（缓变）流方程式：

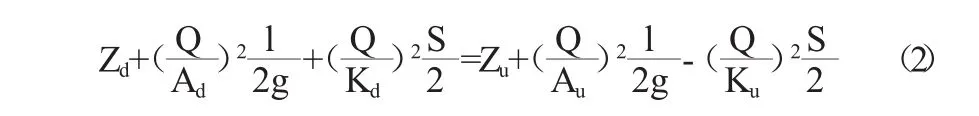
用（2）式计算出的各断面水位即为非恒定流计算的初始条件。

②第一边界条件：第一边界条件为入流断面的洪水过程，采用水库设计1000年一遇洪水，因洪水过程较长，而计算时段较短，只选取入库最大洪峰前后的几个时段进行计算，当时段为30min时，流量过程为13350，14440，15528，16183，16838，17925，18983，17660，16336，14671，单位为m3/s。

③第二边界条件：第二边界条件为泄洪闸闸门全开时的水位～泄量关系，可由公式确定，即q=f（z）。

3.5 计算时段Δt的确定

计算入流断面选定在66号断面，末断面为1号断面（即坝前）全流程距离16660m。Δt的大小由微波公式决定：

其中Q为恒定流流量，A为过水断面平均面积，可概化为矩形断面，即A＝Bh，B为平均断面宽度，h为全流程平均水深。

已知：S＝16660m，Q＝6145m3/s，B＝4000m，h＝8.5m， g＝9.8m/s2

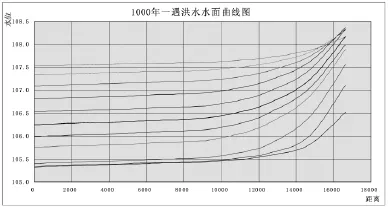
图1 1000年一遇洪水水面曲线图

将这些数据代入上式得：Δt＝1790s

因此，Δt取近似值1800s，即半小时。

3.6 编程计算

计算时由于断面多、工作量大，手工计算几乎不可能，因此要用计算机编程计算。根据计算经验，如果从入流断面（即末断面）计算至出流断面（即起始断面），因（1）式为多解，且具有发散性，为提高运算速度，在编程时采用“逆算法”，即从1号断面算至入流断面。为便于处理将式（1）整理为：

再结合初始条件、第一、第二边界条件就可对式（3）求解。

具体思路是：先假设第一时段末1号断面水位Zd"，代入第二边界条件可以求出Qd"，再结合断面特征资料及初始条件可计算出的本流段的初始V'，这样就可根据式（3）试算出第二断面的Zu"，再由（1）式求出Qu"。然后依次向上断面计算，直至算到入流断面（66号断面）。比较算出的Qu"与第一边界条件是否相符，如果结果小于设定误差，第一时段的计算结束，进行下一时段计算；如果不等，重新假设1号断面时段末水位，再重复上述计算步骤，直至相符。其他时段的计算与第一时段方法相同，只是初始条件已经变化为本时段末各断面的水位和流量。

4 非恒定流计算结果

将准备好的有关资料（粗糙率、水位～面积、水位～湿周等）及各频率的初始条件及边界条件按要求输入到计算机中，并启动水面线计算软件即可算出结果。该结果为各时段末、各断面的水位及流量。因结果数据较多，这里仅整理出部分数据，作出曲线图如图1。

5 结语

非恒定流水面线是动态的，其形状随时间不断变化，从计算结果中可以看出来。由此表可知，分洪段（56号断面）与拦河坝前水位差最大可达0.548m，时间发生在第90min（即第三时段末），此时出入流断面也发生了最大水位差2.147m。其他时段的水位差则均在0.26m以上。

一般来讲，水库的上下游水位差除与入库流量大小有关外，还与流量过程线的形状有关，形状越陡，差值越大，计算结果基本上反映了这个规律。

白龟山水库目前只观测拦坝水位，在选定的其他断面内没有水位观测站，计算结果是否精确无法用实测资料来校核，但计算是依据水力学中成熟的理论，只要有关参数选择合适，其结果不会有太大的偏差，对水库调度具有一定的参考价值。当然，影响计算结果精度的因素很多：一是库区内糙率值的选定是否合理；二是计算条件的确定，尤其是非恒定流的初始条件是假设的；三是假定水流是缓变的，而实际不尽然。以上这些因素对计算结果都将产生不利影响