基于模糊综合评判的野战油库选址优化模型
2015-12-23程飞,丁国勤,李宁等
【后勤保障与装备管理】
基于模糊综合评判的野战油库选址优化模型
程飞,丁国勤,李宁,郭骏骏,杨帆
(中国人民解放军后勤工程学院,重庆401331)
摘要:作战后勤保障中,野战油库作为连接后方基地与作战前线之间的可移动油料仓库直接关系到部队作战效能的发挥,选址又是野战油库开设中最基础、最重要的环节。基于模糊综合评判思想,对野战油库选址要素进行分析,构建了模糊综合评判指标体系,确定了隶属函数及指标权重,建立了野战油库选址模糊综合评判模型。实例验证表明,基于模糊综合评判的野战油库选址模型为野战油库选址提供了一种有效的方法。
关键词:野战油库;选址优化;模糊综合评价
收稿日期:2014-11-26
作者简介:程飞(1963—),男,高级工程师,主要从事教学管理和油料管理研究。
doi:10.11809/scbgxb2015.06.014
中图分类号:E239
文章编号:1006-0707(2015)06-0053-06
d oiKey words: fiell depot; optimized site selection; fuzzy comprehensive assessment
本文引用格式:程飞,丁国勤,李宁,等.基于模糊综合评判的野战油库选址优化模型[J].四川兵工学报,2015(6):53-57.
Citation format:CHENG Fei, DING Guo-qin, LI Ning, et al.Optimized Site Selection Model Research of Field Oil Depot Based on Fuzzy Comprehensive Assessment[J].Journal of Sichuan Ordnance,2015(6):53-57.
Optimized Site Selection Model Research of Field Oil Depot
Based on Fuzzy Comprehensive Assessment
CHENG Fei, DING Guo-qin, LI Ning, GUO Jun-jun, YANG Fan
(Logistical Engineering University of PLA, Chongqing 401331, China)
Abstract:As the mobile oil depot between rear base and frontline combat, field oil depot is one of a POL support entity and directly related to the effective performance of troops in battle logistics support, and site selection research is one of the most important and most fundamental problems. Based on the fuzzy comprehensive assessment, this article analyzed the site selection factors of field oil depot and constructed the fuzzy comprehensive index system of evaluation. Then discussed the general method of determining membership function and index weight and established the location model. Instance proves that the optimized site selection model of field oil depot based on the fuzzy comprehensive assessment is an effective method.
随着我军现代化建设的进一步深入,对后勤保障的要求越来越高,油料作为现代战争的血液,在后勤保障中占有重要地位[1]。作为连接后方基地与一线部队之间的可移动油料仓库,野战油库这一保障实体的油料保障快速性直接关系到部队作战效能的发挥。对野战油库进行研究有着重要的理论价值和现实意义。而选址是野战油库开设中的一项重要工作,库址选择的好坏,不仅关系到野战油库工艺流程的走向、展开的难易程度,油库的安全以及补给的经济性都有很大的影响[2]。也将影响到开设进度乃至作战油料保障任务的完成,甚至可能影响到作战的进程和结局。
本研究基于模糊综合评判思想,对野战油库选址要素进行分析,构建了模糊综合评判指标体系,探讨确定了隶属函数及指标权重,建立了野战油库选址模糊综合评判模型。实例验证充分说明了基于模糊综合评判的野战油库选址模型为野战油库选址提供了一种有效的方法。
1模糊综合评判
模糊数学是研究和处理模糊现象的一种数学方法,所谓模糊现象即是不能简单的定量描述的现象,例如在日常生活中的好与坏、大与小、快与慢、长与短等都包含着一定的模糊概念[3]。
1.1模糊数学的基本概念
定义1如果将所讨论的对象限制在一定的范围内,并记所讨论的对象全体构成的集合为U,称之为论域。所谓论域U上的模糊集A是指:对任意x∈U总以某个程度uA(uA∈[0,1])属于A,而非x∈A或x∉A。

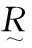

1.2模糊综合评判的一般步骤
模糊综合评判一般依据确定因素集、评判集、模糊综合评判矩阵最后进行综合评判的流程进行,其流程如图1所示。

图1 模糊综合评判方法流程
步骤1:确定因素集U={u1,u2,…,un};
因素集,由研究对象的n种因素(或指标)构成,其中ui(i=1,2,…,n)代表第i个因素。
步骤2:确定评判集V={v1,v2,…,vm};
对于不同的研究对象,不同的评价因素(或指标),评判集的构成也不同。例如由5个元素组成的评判集,可以是{很好,好,一般,差,很差}、{很高,高,一般,低,很低}等。
步骤3:确定模糊综合评判矩阵R=(rij)m×n;
首先,对每一个因素ui做一个评判f(ui)(i=1,2,…,n),则可以得到U到V的一个模糊映射f(隶属函数)。然后,由模糊映射f可以诱导出模糊关系Rf∈F(U×V),
Rf(ui,vj)=f(ui)(vj)=rij(i=1,2,…,n;j=1,2,…,m)因此可以确定出模糊评判矩阵R=(rij)m×n,而且称(U,V,R)为模糊综合评价模型,U,V,R称为该模型的三要素。
步骤4:综合评判;
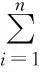
2野战油库选址模型建立于求解
2.1野战油库选址要素分析
2.1.1自然环境要素[4]
1) 位置适宜
野战油库应选择在主要作战方向便于机动的位置上,同时兼顾次要方向;既便于对下供应,又便于上级补给;既便于保障当前,又便于兼顾尔后任务的发展和变化。在满足战略战役意图要求的前提下,油库的位置应尽量避开大、中城市、大型工矿基地、重要的交通枢纽、大型水库、桥梁、名胜古迹和其他容易遭空袭的目标[5]。
2) 地形有利
野战油库要求隐蔽,对空自然防护能力强。最好选择在具有良好自然防护条件的山地、丘陵地、森林地。应有充足、可靠的水源,并要满足饮用的卫生要求,以保障库区消防、作业和生活用水需求。
3) 交通方便
战时条件下,要求迅速的组织油料保障,时效性较强。因此,野战油库应靠近主要的公路或水、陆交叉点,有条件时可以争取靠近铁路,以保证基地后方基地对野战油库的补给。同时,库区内道路应通畅,能同时容纳多台车作业。
4) 地幅适当
库区应能同时展开多个的软体油罐,同时留有相应的作业空间,以保证野战油库能正常工作,且便于警戒防御。
2.1.2非自然环境因素
1) 民情社情
库址应选择在社会治安良好,居民素质较高的地区,以免不必要的麻烦和经济损失。
2) 与作战前沿距离适当
野战油库与作战前沿应保持一定的距离,一般情况下200 km左右最为恰当。当野战油库距作战前沿较远时,会出现油料保障实施难度较大、油料补给不及时等后果,不能持续、快速的保障部队作战用油,影响战争进程。然而,当野战油库距作战前沿较近时,由于油库自身防护能力差,又是敌打击的重点,野战油库便很容易暴露目标遭受炮火袭击。
3) 与后方基地距离较近
在与作战前沿保持适当距离的前提下,野战油库距离后方基地不应太远,以保证后方基地、野战油库及前线的良好衔接和油料的持续补给。
2.2模糊综合评判指标体系的确定
本研究对模糊的指标进行分层、量化与归一,使各指标量化为[0,1],最终确定了选址评估指标体系[6]。根据前分文析,得到如图2所示的指标网络。
图2野战油库选址指标网络
然后,将得到的18个二级指标编号并进行归类。B1,B2,B3,C1,C2,D4,E1,E2共8个二级指标不能直接量化,应将其分为5个等级,分别为很好、好、较好、一般、差,其对应的值分别确定为0.95、0.85、0.75、0.65、0.55,按照军事后勤理论和油料勤务理论,参照以往野战油库选址的经验,专家评分,最终确定量化指标。
A2,A3,A4,B4共4个二级指标属于可以量化的正向指标(其值越大越好),A1,D1,D2,D3,E4共5个二级指标属于可以量化的反向指标(其值越小越好)。E3这个指标属于可以量化的中性指标(E3的值约为200 km最好)。对于正向指标和反向指标的量化归一基本思想是:对于可以量化的正向指标和反向指标,确定出其最大值和最小值,把最大值对应设为1,最小值对应设为0(对应正向指标),或把最大值设为0,最小值设为1(对应反向指标),实际值就参照对应比例进行放大或缩小为0-1之间的值。例如靠近公路(D1)这个二级指标的量化处理过程为:最大值定为≥10 km(对应处理后的指标值为0),最小值定为≤1km(对应处理后的指标值为1),当1
所有二级指标经过量化归一处理后,均变成了正向指标,其生成值都在0-1之间,且具有相同的量纲,从而相互间具备了一致性和可比性。从而最终确定量化指标(i=1,2,…,18)。
2.3因素集U与评判集V的确定
在野战油库选址的模型中,在主要作战方向上(A1),避免大中城市(A2)等共18个二级指标构成了模糊综合评判指标体系,从而构成了因素集。因此u1=A1,u2=A2,…,u18=E4,即因素集U={A1,A2,…,E4}。
针对野战油库的选址问题,研究对象为库址的选择,其结果有好坏之分,因此其评判集可以由“很好、好、较好、一般、差”这5级构成。也可以将评判集量化,即“[0.9,1],[0.8,0.9],[0.7,0.8],[0.6,0.7],[0,0.6]”。所以V={很好、好、较好、一般、差}或V={[0.9,1],[0.8,0.9],[0.7,0.8],[0.6,0.7],[0,0.6]}。
2.4隶属函数的确定
确立符合实际的隶属函数是应用模糊数学方法建立数学模型的关键,隶属函数形式有多种,如戒上型、戒下型、正态型、Γ型等[7]。在实际应用中,为方便起见常采用梯形、三角形较多,通常采用如图3所示的5种形式。

图3 5种常用的隶属函数
在研究中,将评判集V确定为5级,即V={很好、好、较好、一般、差}。所以隶属函数f(xi)∈[0,1]应该分成5段,每一段隶属函数分别对应评判集中的一个元素。
又V={[0.9,1],[0.8,0.9],[0.7,0.8],[0.6,0.7],[0,0.6]},所以5段隶属函数的拐点可确定为0.55、0.65、0.75、0.85、0.95,分别用a,b,c,d,e表示。利用梯形、三角形作为隶属函数时,第一段采用Z型,第5段采用S型,中间3段采用Λ型较为合适。如图4是野战油库选址模型的隶属函数图。

图4 野战油库选址模型的隶属函数图
该隶属函数的5个分段函数公式如下:
(1)
(2)
(3)
(4)
(5)
式中,xi(i=1,2,…,18)为因素ui对应的指标值。
2.5建立关系模糊矩阵
因素集U={A1,A2,…,E4},评判集为V={[0.9,1],[0.8,0.9],[0.7,0.8],[0.6,0.7],[0,0.6]}。通过隶属函数(1)-(5)分别求出单个因素ui对于5个评价等级的隶属度,得到一个18×5的关系模糊矩阵Rk∈F(U×V)(k表示第k个野战油库选址的候选地域),即
(6)
2.6各指标权重的确定
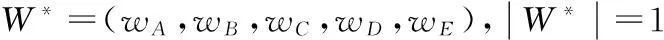
2.7模型的建立与求解
分别确定了基于模糊综合评判的野战油库选址模型的指标体系、因素集、评判集、隶属函数、关系模糊矩阵及指标权重。基于此,对于第k个野战油库选址候选地域,建立评判模型
(7)
即隶属度向量。式中:k代表野战油库选址候选地域;wi(i=1,2,…,18)为权重;rij(j=1,2,…,5)为关系模糊矩阵Rk的元素。
将所有q综合,得到野战油库选址模型的评判矩阵(或隶属度矩阵)
(8)
式中,l表示野战油库选址候选地域的数量。
该模型涉及的均为矩阵的简单运算,本研究利用Matlab软件编程进行优化求解。
3野战油库选址模型的实例分析
假设某次行动中,要在8个预配置地域(分别定义为M1,M2,…,M8)内,选择其中一处,作为野战油库地点。按前文节描述的方法,量化归一处理后得到表1,由多名专家评分并统计分析后得到表2。

表1 模糊综合评判指标值

续表

表2 各级指标的权重值( W/ w)
再对每一个野战油库候选地域(以M1为例),将表1中的数据分别代入隶属函数式(1)~式(5)即可得到关系模糊矩阵,例如M1的关系模糊矩阵可表示为
将表2中的数据代入权重向量公式W=(wA·W1,wB·W2,wC·W3,wD·W4,wE·W5)得到权重向量W=(w1,w2,…,w18)=(0.12,0.06,0.045,0.075,0.035,0.015,0.03,0.02,0.1,0.1,0.0875,0.05,0.0625,0.05,0.015,0.06,0.06)。
对于候选地域M1,得到评判模型:
即q1=(0.301 5, 0.09, 0.235 5, 0.359 75, 0.013 25)。利用同样的方法,可以得到其余7个候选地域的隶属度向量,最终得到评判矩阵(或隶属度矩阵)。根据最大隶属原则,得到评判结果如表3所示。
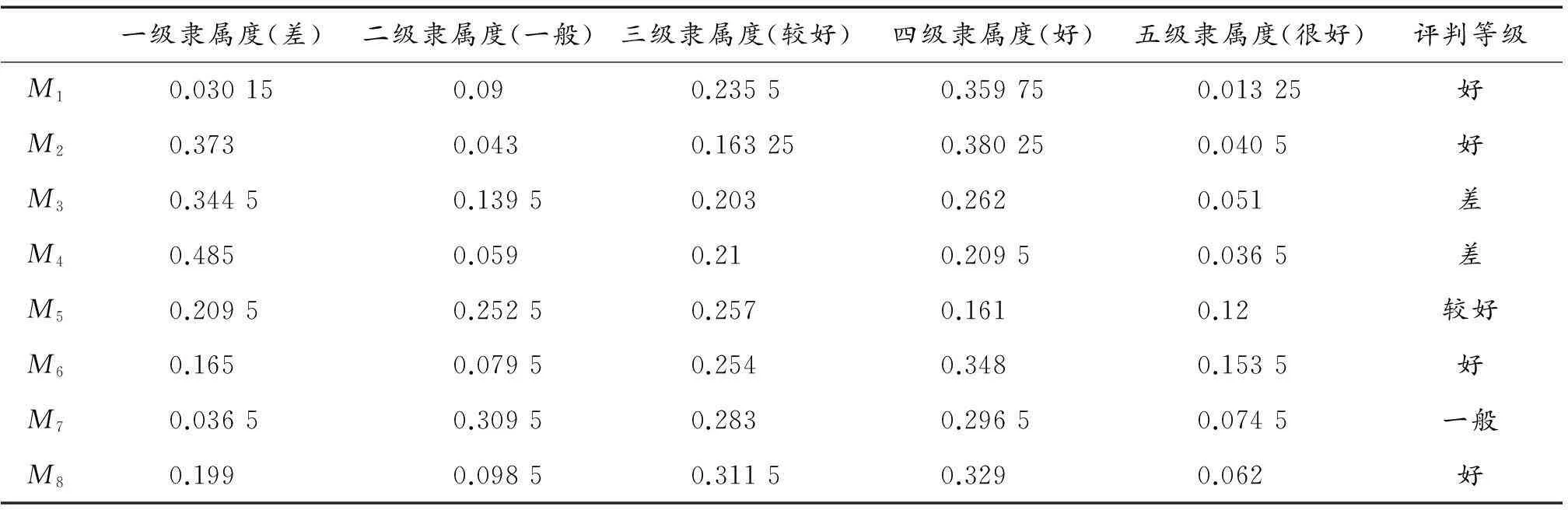
表3 野战油库选址模型的评判结果
以M1为例,“差”对于评判集V={很好、好、较好、一般、差}的隶属度为0.030 15,“一般”对于评判集的隶属度为0.09,“较好”对于评判集的隶属度为0.235 5,“好”对于评判集的隶属度为0.359 75,“好”对于评判集的隶属度为0.013 25。此时可以用概率的概念近似理解,如野战油库候选地域M1为差的概率是3.015%,为一般的概率是9%等。因此,一级隶属度值越小越好,二级隶属度值呈中性,三级、四级、五级隶属度值依次越来越大最好。
从表3可以得到各候选地域的评判等级,M1,M2,M6,M8的评判等级为四级(好),M5的评判等级为三级(较好),M7的评判等级为二级(一般),M3,M4的评判等级为一级(差)。所以M1,M2,M6,M8优于M5,M5优于M7,M7优于M3,M4。但对于具有相同评判等级的候选地域,确不能简单地依靠隶属度值进行优劣排序。如M3与M4,M3大于M4的二级、四级、五级隶属度值,而它的一级、三级隶属度值确小于M4的,因此无法确定M3与M4的优劣。这便是最大隶属原则较加权平均法的不足。对于M2,M6,M8,虽然评判等级为四级(好),但一级隶属度值较大。特别是M2,一级隶属度值达到0.373,与四级隶属度值0.380 25相当。从渐变性的角度考虑,M2有向“差”发展的趋势。M2便是指标值两级分化的地域,即M2的部分指标较优、部分指标又相当劣,因此应淘汰M2。当采用加权平均法时,若各指标权重确定不当,M2有可能作为最优的对象成为油库选址地域。最大隶属原则不存在这种现象。
综上所述M1可以作为野战油库选址地域,M6,M8这2个地域作为备选方案。
4结论
模糊综合评判是一种对受多种因素影响的事物做出全面评价的有效地多因素决策方法,能够较好的解决野战油库选址问题。本研究基于模糊综合评判思想,首先,通过对野战油库选址要素的分析、模型的假设、指标体系的确定、隶属函数的确定等过程,为模型的建立打下了基础。其次,针对每一个候选地域,建立评判模型,得到隶属度向量,并综合所有的候选地域得到评判矩阵。最后,通过实例进一步阐述了野战油库选址模型的解题方法及具体步骤。
参考文献:
[1]仰勇,周庆忠,苗强,等.鲍摩-瓦尔夫模型在野战油库选址中的应用[J].后勤工程学院学报,2009,25(4):41-44.
[2]郭海华,吴家锋,徐华.基于层次分析法的机场野战油库选址研究[J].军事物流,2009(1):121-122.
[3]韩中庚.数学建模方法及应用[M].北京:高等教育出版社,2005:322-335.
[4]韩亮,蔡禹.组合式战役野战油库选址时应注意的问题[J].军用航油,2008(6):50-50.
[5]周庆忠.作战油料分析[M].北京:解放军出版社,2008:189-228.
[6]彭波,张国盛,汪涛,等.基于人工神经网络的野战油库选址评估模型[J].海军后勤学报,2006(2):35-37.
[7]ChengHD,ChenJR.Automaticallydeterminethemembershipfunctionbasedonthemaximumentropyprinciple[J].InformationSciences,1997,3-4(96):163-182.
[8]吴万钊.模糊数学与计算机应用[M].北京:电子工业出版社,1988:56-57.
[9]郭滕达,杨清清,蔡瑞辉.基于网络层次分析的军事逆向物流中心选址方法[J].兵工自动化,2014(2):30-34.
(责任编辑杨继森)
