某圆柱壳体结构加筋拓扑优化分析

【机械制造与检测技术】

某圆柱壳体结构加筋拓扑优化分析

马青，王涛

(中国科学院 长春光学精密机械与物理研究所，长春130033)

摘要：加筋圆柱壳结构在飞行器中大量使用。为了确定某圆柱壳体结构的筋的分布，运用SIMP材料插值方法对其进行了拓扑优化分析。以筋在优化区域内的分布为优化变量，以筋的总体积不超过优化部件总体积的50%为约束条件，以低阶固有频率最大化为优化目标，对圆柱壳体结构进行拓扑优化，优化后的低阶固有频率由优化前的357Hz增加到386.4Hz，增加了8.24%。

关键词：拓扑优化；有限元；固有频率

作者简介：马青(1987—)，女，硕士，研究实习员，主要从事计算固体力学研究。

doi:10.11809/scbgxb2015.09.020

中图分类号：TP391.7

文章编号：1006-0707(2015)09-0079-03

本文引用格式：马青，王涛.某圆柱壳体结构加筋拓扑优化分析[J].四川兵工学报，2015(9):79-81.

Citation format:MA Qing, WANG Tao.Reinforced Topology Optimization Analysis of A Cylindrical Shell[J].Journal of Sichuan Ordnance,2015(9):79-81.

Reinforced Topology Optimization Analysis of A Cylindrical Shell

MA Qing, WANG Tao

(Changchun Institute of Optics, Fine Mechanics and Physics,

Chinese Academy of Sciences, Changchun 130033, China)

Abstract:Stiffened cylinder shells are widely used in aircraft. SIMP method was employed in topology optimization analysis of a cylindrical shell to identify locations for reinforcer in the designable region. The design variables were the locations for reinforcer in the design space. The constraint was upper bound constraint of 50% for the designable volume. The objective was to maximize frequency of mode number one. The result is the frequency of the structure for the first mode has increased from 375Hz to 386.4Hz. The natural frequency is increased by 8.24%.

Key words: topology optimization; finite element; natural frequencies

随着航空、航天各类飞行器对飞行性能、比强度、比刚度等方面提出愈来愈高的要求，结构设计的要求也越来越高[1]。在航空、宇航结构中，加筋板壳是飞行器中常见的一种结构形式[2]，它可以在减轻结构质量的同时，保证飞行器的强度和刚度满足规定的要求。

结构拓扑优化设计实际上就是材料在设计空间的分布优化问题[3]。1904年Michell提出析架理论[4]，20世纪60年代初Schmit将结构优化问题表述为数学规划问题，并采用数学规划算法求解[5]。Mlejnek等[6]从工程角度出发提出了结构材料密度的幂次惩罚模型，通过在0-1离散结构优化问题中引入连续设计变量，并加入中间密度惩罚项，从而将离散结构优化问题转换为连续结构优化问题。Sigmund和Bendsoe等[7-9]提出了一种基于正交各向同性材料密度幂指数形式的变密度法材料密度插值理论，又称为SIMP理论。

运用SIMP材料插值方法对飞行器中的某圆柱壳体结构进行拓扑优化分析，确定筋的分布位置。

1SIMP材料插值方法的结构拓扑优化模型

结构的拓扑优化问题实际上是一个单元集合的有无和增减问题，通过不断地优化迭代计算，保留对结构传力路径有利的结构单元，而删除对结构传力路径作用不大的单元。因此从本质上来说，结构的拓扑优化问题是一个包含单元增删的离散型优化问题[10]。

体积约束情况下离散结构的拓扑优化问题可表达为

(1)

问题(1)是一个0-1离散变量优化问题，在大规模情况下，由于缺乏一种有效的大规模离散变量优化算法，离散变量优化设计往往失败，通常都得不到问题的确切解。因此必须将离散变量优化问题(1)转换为连续变量优化问题，以充分利用一些现有的有效数学规划算法。除了材料密度为0和1的单元外，通过引入中间连续型材料密度单元，对设计变量进行放松，将设计变量变化域由ρ=0或1转换为0≤ρ≤1，并且采用不同的插值方法建立中间密度单元与其单元性能属性之间的数学关系式。这样通过引入中间密度单元，就将离散型优化问题转换为连续型优化问题，而实际上中间密度单元是无法存在和制造的，因此又要尽量避免中间密度单元的产生，减少中间密度单元的数目，这时就需要对设计变量中出现的中间密度值进行限制的惩罚项。

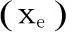
在上述假设前提下每个单元只包含一个设计变量，相对于均匀化方法而言，减少了设计变量的数目，同时单元相对密度变化后，对应的材料属性可表示为初始材料属性和单元相对密度的指数函数关系，简化了计算求解过程。

2建立有限元模型

将圆柱壳体的CAD模型导入到HeperMesh中，在HeperMesh中选用四边形和三角形混合网格进行自动划分，网格尺寸为3mm。如图1所示，为圆柱壳体的有限元模型。

图1　圆柱壳体有限元模型

圆柱壳体采用铝合金加工而成，材料的主要参数见表1所示。

表1　材料主要参数

3圆柱壳体结构拓扑优化分析

本研究对圆柱壳体加筋结构进行了优化，使其在约束条件下的一阶固有频率最大，优化过程如下：

1) 载荷及约束

圆柱壳体在自由振动状态下没有激励，故不施加任何载荷和约束。

2) 定义优化变量

以圆柱壳体作为优化区域，在优化区域中壳体的厚度为1mm，加筋处厚度最大可达3mm。

3) 定义约束条件

在本次优化中，为满足飞行器的质量要求，故将所增加的筋的总体积不超过优化部件总体积的50%作为约束条件。

4) 定义优化目标

由于对圆柱壳体没有施加任何载荷和约束，导致圆柱壳体发生了刚体位移，故前6阶固有频率为零，所以只从第7阶固有频率开始分析。以第7阶固有频率最大化为优化目标。

5) 优化结果

如图2所示为拓扑优化的结果图，图2中显示了各个方向的优化分析结果。从图2中可以看出需要加筋的部分主要分布在圆柱壳体的两端，筋的厚度最大可为3mm，显示为红色区域，主要分布在2个部分。其一，在圆柱壳体的圆柱面部分，沿轴向均匀分布在壳体的表面，并与轴向平行；其二，圆柱面部分与锥面部分的交界处，沿壳体周向分布。从图2中还可以看出，越靠近圆柱端面，筋的密度越大。

优化前导弹的第7阶固有频率为357Hz，优化后导弹的第7阶固有频率为386.4Hz，增加了8.24%。

图2　拓扑优化结果

4结论

结合飞行器的质量要求，以筋在优化区域内的分布为优化变量，以筋的总体积不超过优化部件总体积的50%为约束条件，以低阶固有频率最大化为优化目标，运用SIMP材料插值方法对圆柱壳体结构进行拓扑优化分析，使圆柱壳体结构在要求的体积和质量范围内，其低阶固有频率由优化前的357Hz增加到386.4Hz，增加了8.24%，从优化的结果中可以看出越靠近圆柱端面，筋的密度越大，且沿轴向均匀分布。本研究所述的拓扑优化分析方法还可以结合圆柱壳体结构固有频率的实测数据进行优化迭代，迅速找到合适的筋的分布。

参考文献：

[1]闫光.轴压载荷下复合材料层合圆柱壳的设计与试验研究[D].长春:吉林大学,2013.

[2]韩涵.运载火箭加筋壳结构稳定性分析[D].长沙：国防科学技术大学,2005.

[3]BendsoeMP.Optimalshapedesignasamaterialdistributionproblem[J].StructuralOptimization,1989(1):193- 202.

[4]MichellAGM.Thelimitsofeconomyofmaterialsinframestructures[J].PhilosophicalMagazine,1904,8(47):589-597.

[5]SchmitLA.Structuraloptimization-someideasandinsights[C]//NewDirectioninOptimumDesign.US:NewYork:1984.

[6]MlejnekHP,SchirrmacherR.Anengineeringapproachtooptimalmaterialdistributionandshapefinding[J].ComputerMethodsinAppliedMechanicsandEngineering.1993,106(2):1-26.

[7]SigmundO.Designofmaterialstructuresusingtopologyoptimization[D].Denmark:TechnicalUniversityofDenmark,

1994.

[8]BendsoeMP,SigmundO.Materialinterpolationsintopologyoptimization[J].ArchiveofAppliedMechanics,1999,69:635-654.

[9]RietzA.SufficiencyofafiniteexponentinSIMP(powerlaw)methods[J].Struct.Multidisc.Optim.,2001,21:159-163.

[10]左孔天.连续体结构拓扑优化理论与应用研究[D].武汉：华中科技大学,2004.

(责任编辑唐定国)