基于Bayes理论改进的系统可靠性综合MML法

【基础理论与应用研究】

基于Bayes理论改进的系统可靠性综合MML法

杨仁

(中船重工第710研究所, 湖北 宜昌443003)

摘要：针对可靠性综合MML法面对无失效数据时存在的不足，提出了基于Bayes理论改进的MML法，利用Bayes方法对0失效单元的可靠度进行点估计，通过实例验证了改进的合理性，因其利用了验前信息，避免了直接利用试验数据导致的冒进且也不保守，能够较好的解决试验结果中零失效的情况；应用改进后的MML法关键是要正确利用验前信息，才能使系统可靠性综合结果真实反映产品可靠性水平。

关键词：Bayes理论；可靠性综合；MML法；数据转换

收稿日期：2015-02-17

作者简介：杨仁(1980—)，男，高级工程师，主要从事质量与可靠性研究。

doi:10.11809/scbgxb2015.09.039

中图分类号：TJ610

文章编号：1006-0707(2015)09-0158-04

收稿日期：2015-03-20

基金项目全军军事类研究生资助课题“陆军无人化作战体系效能评估方法研究”(2014JY185)

本文引用格式：杨仁.基于Bayes理论改进的系统可靠性综合MML法[J].四川兵工学报，2015(9):158-161.

Citationformat:YANGRen.ImprovedMMLMethodofSystemReliabilitySynthesisBasedonBayesianTheory[J].JournalofSichuanOrdnance,2015(9):158-161.

ImprovedMMLMethodofSystemReliabilitySynthesis

BasedonBayesianTheory

YANGRen

(No.710ResearchandDevelopmentInstitute,ChinaShipbuildingIndustryCorporation,Yichang443003,China)

Abstract:In order to solve the problem that MML method cannot be directly used for reliability synthesis in the case of zero-failure date, an improved MML method based on Bayesian theory was proposed, and it used Bayesian method to estimate the reliability of zero-failure unit. Through analysis and comparison, the rationality of improved MML method had been validated. The results are neither aggressive nor conservative. In order to make the reliability synthesis more close to the true value, the prior information should be used correctly.

Keywords：Bayesiantheory;reliabilitysynthesis;MMLmethod;datetransform

系统可靠性综合评估通常采用“金字塔”式的评估模式[1]，按照组部件——分系统——系统的顺序，依据系统可靠性结构框图逐级向高一级进行可靠性综合，最后得出系统的可靠性评估值。

鱼雷、水雷等现代武器装备，采用的技术越来越先进，结构越来越复杂且可靠性指标也越来越高，分配到各分系统、组部件的可靠性指标就更高，按传统的评估方法需要的样本量将十分惊人，成本非常之高昂，采购方和承制方都难以接受，因此采用适宜的可靠性综合方法对系统可靠性指标进行评估成为一种可行的方式。目前，工程上进行系统可靠性综合常用的方法有：MML法(修正极大似然估计方法)、SR法(逐次压缩方法)、L-M(Lindstrom)方法等，通过随机模拟比较，MML方法是成败型串联系统几种偏保守方法中最不保守的[2]，即近似限比较准确，但是存在不能考虑无失效单元的缺点。在高可靠性产品试验时，出现0失效单元的情况是经常存在的，因此需要对MML法进行优化以提高其适应性。本文基于Bayes理论提出了MML法的一种改进方法，弥补其在高可靠性产品系统可靠性综合时存在的不足。

1试验数据等效转换

可靠性综合评估的首要工作是将不同类型的试验数据等效转换为统一类型的试验数据，对成败型产品进行可靠性综合，按照单元服从总体的思路，需要把系统组成单元、部件的非成败型试验数据按照一定的方法折算为成败型数据进行处理；另一方面，在不知道产品的寿命分布时，如果取产品的试验时间等于任务时间，并在试验时间终止时记录产品是否失效，这样得到的试验数据即为成败型数据。MML法是将系统看作二项分布进行系统可靠性综合，对于非成败型数据需要将其转化为成败型数据，目前常用的转换方法是点估计下限法[3]：

对成败型产品，假设进行了N次试验，成功了S次，则可靠度的极大似然估计为

(1)

其置信度为γ的经典非随机化可靠度最优置信下限RLC为[4]

(2)

在已知待转换单元的寿命分布时，可以按照该分布特征求可靠度极大似然估计值及其置信下限，基于可靠度极大似然估计和γ置信度下可靠度最优置信下限分别相等的思想，可以建立如下等效数据转换公式：

(3)

用不完全贝塔函数还可以表示为

(4)

其中， N′为折算成成败型试验的等效试验次数，S′等效成功次数,N′，S′可取非负小数。

2MML综合方法的不足与改进

2.1MML综合方法介绍

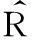
(5)

(6)

(7)

则系统级的等效试验数N，失效数F分别为

(8)

其中：(ni,fi)为第i个单元的试验数及失效数，i=1,2，…，m。(n0,f0)为系统级试验数及失效数。

现假定某系统由3个单元串联组成，系统级试验数据为(2,0)，3个单元试验数据分别为：n1(5,0)、n2(10,0)、n3(60,0)，求置信度γ=0.7时的系统可靠度下限。

针对上述试验数据，用MML综合方法式(7)可以发现分子和分母都出现了为0的情况，此时MML法根本无法用；若仅有个别单元失效数为0时，其可靠度的极大似然估计为1，计算结果显然会比较冒进。

此例虽然可以利用L-M法进行综合，但若各单元的试验数据为n1(5,0)、n2(5,0)、n3(5,0)时，通过计算可以看出，应用L-M计算的系统可靠度下限完全一致，也就说单元2、3进行10次、60次无故障试验与均进行5次无故障试验评估出的系统可靠度置信下限是一样的，这显然没有充分利用单元的试验信息，评估的结果比较保守。

MML法作为系统可靠性综合中一种较好的方法，唯一的不足是没有考虑0失效单元。因此，针对高可靠性产品经常出现0失效单元的情况，需要对MML法做适当改进，才能扩大其应用范围，得到较为精确的评估结果。

2.2改进的MML综合方法

MML法的不足在于对0失效单元可靠度的点估计上，当失效数为0时，其极大似然估计为1，显然不合理，而且0失效单元越多，利用MML法得到的可靠性结果无疑是很冒进的。因此0失效单元不能简单的用1作为其可靠度点估计，一个单元出现0失效说明其可靠度较高，而且随着试验量越大，其可靠度值越大，越接近1，但不能等于1，此时我们可以利用Bayes方法对0失效单元进行点估计，使其更接近真值。此处以二项分布为例，其他分布试验数据可以转化为二项分布试验数据。二项分布的共轭验前分布服从β(R|s0,f0)[6]，有先验信息时根据先验信息求出参数(s0,f0)。

当无先验信息时，验前分布有3种取法[7]，即

1) Reformulation 方法：

2) Box-Tiao方法：

3) Bayes假设：

在以上3种方法中，Box-Tiao方法评定结果与精确置信限最接近，因此建议采用Box-Tiao方法进行无信息Bayes评定[8]。

设产品的成功率为R，对其进行n次试验，失效f次，记为(n，f)，其似然函数为

(9)

先验分布为π0(R)时，其后验分布为

(10)

在平方损失函数下，参数R的Bayes估计为

(11)

先验分布采用Box-Tiao方法选取时，R的点估计为

(12)

基于Bayes理论改进的MML法主要是对0失效单元点估计的计算，改进后的MML公式

(13)

式(13)中

当单元的失效数为0时，由于Bayes评定理论利用了验前信息，使0失效单元的点估计无限接近1而非1，避免了评定结果的冒进性。

3实例分析

某型武器装备由电子单元(指数分布)、安全保险单元(二项分布)、火工品动作单元(二项分布)、火箭发动机(二项分布)4个单元串联组成，其中系统级试验进行了10次，失效0次，各组成单元试验数据如下：

电子单元：试验T=3 120 h，失效r=1次，任务时间为t0=100 h；

安全保险单元：试验n2=100次，失效f2=1次；

火工品动作单元：试验n3=60次，失效f3=0次；

火箭发动机：试验n3=40次，失效f3=0次；

试评估γ=0.7时，系统可靠度置信下限。

根据试验数据可以发现，4个单元中只有电子单元试验数据需要转换为成败型数据，计算步骤如下：

可靠度置信下限：

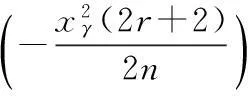
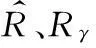
下面分别用改进MML法、MML-SR、L-M法对该系统进行可靠性综合：

1) 采用改进MML法。4个单元中火工品动作单元和火箭发动机在试验中均出现了失效数为0的情况，因此需要利用Bayes方法求点估计，在此试验前虽然进行了部分试验，但技术状态未完全固化，且出现故障后进行了改进，这里按无验前信息进行处理，采用Box-Tiao方法，计算可得：

利用式(13)计算得系统等效试验数：N′=41.03, F′=2.49

综合后系统级的试验数和失效数分别为

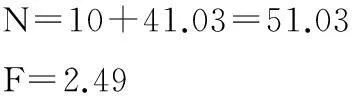
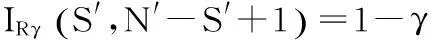
2) 采用CMSR法[9]。由于上述试验数据中，无失效单元的试验次数不是最小的，因此MML-SR法不对试验数据进行压缩，计算公式等同与MML法，试验数据带入式(7)计算得：

系统等效试验数和失效数分别为N′=38.12, F′=1.57。

则系统级的试验数和失效数分别为N=48.12, F=1.57。

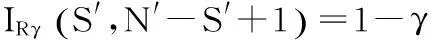
由于MML-SR法未对无失效单元试验数据进行压缩，仍然采用MML法公式进行计算，得到的结果依然有些冒进，由此也可以看出MML-SR法在某些情况下也难以修正MML法存在的冒进估计。

3) 采用L-M法[10]。系统级的等效试验数及失效数分别由下式确定：

试验数据带入上式计算得系统等效试验数和失效数分别为N′=37.71, F′=1.92。

系统级的试验数和失效数分别为N=47.71, F=1.92。

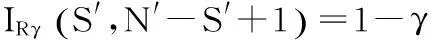
通过3种方法计算比较可以发现：采用改进后的MML法综合得到的结果介于MML-SR法和L-M之间。采用MML-SR法计算时，由于无失效单元的试验次数不是最小的，因此MML-SR法未对无失效单元试验数据进行压缩，仍然直接使用火工品动作单元和火箭发动机的可靠度极大似然点估计1进行计算，因此综合的结果无疑是冒进的；众所周知L-M法计算的结果比较保守，也就是说基于Bayes理论改进的MML法计算的结果介于冒进和保守之间，通过实例可以看出基于Bayes理论改进的MML法的合理性。

4结束语

在武器装备可靠性较高,试验结果中无失效经常存在的情况下，MML法的局限性导致难以直接应用其进行系统可靠性综合，基于Bayes理论改进后的MML法能够较好的解决试验结果中零失效的情况，因其利用了验前信息，避免了直接利用试验数据导致的冒进且也不保守，因此是进行武器装备系统可靠性综合较好的方法。应用改进后的MML法关键是要正确利用验前信息，才能使系统可靠性综合结果真实反应产品实际可靠性水平。

由于系统组成各单元相互间会有影响，各单元独立模拟进行试验很难跟实际情况一致，无论哪种可靠性综合方法都难以考虑这种影响，因此应尽可能多的开展系统级可靠性试验，减少可靠性综合方法无法消除的误差，才能有效提高系统可靠性评估近似限。

参考文献：

[1]王中华.小子样条件下大型复杂系统可靠性评估方法及其在舰船上的运用[D].上海:上海交通大学,2003.

[2]金碧辉.系统可靠性工程[M].北京：国防工业出版社，2004.

[3]陈庆.空间推进系统可靠性评估方法的改进[J].火箭推进 2012(4)：49-55.

[4]周源泉.质量可靠性增长与评定方法[M].北京：北京航空航天大学出版社，1997.

[5]周桂良，黄凯，许琳，等.基于定时、定线路的上下班拼车方案设计与实现[J].重庆工商大学学报：自然科学版，2014，31(12)：54-58.

[6]甄昕，刘孟凯，王淼.可靠性数据常用综合方法研究[J].战术导弹技术 2005(1)：15-19.

[7]张志华.可靠性理论及工程应用[M].北京：科学出版社，2012.

[8]龚庆祥.型号可靠性工程手册[M].北京：国防工业出版社，2007.

[9]金星，洪延姬，张明亮.二项分布单元可靠性评定方法的讨论[C]//全国生产工程第九届年会暨第四届青年科技工作者学术会议论文集，2004，109-112.

[10]潘吉安.可靠性维修性可用性评估手册[M].北京：国防工业出版社，1995.

[11]王鹏，郑贵省，王元.基于ArcGISServer的车辆调度管理系统的设计与实现[J].重庆工商大学学报：自然科学版，2014，31(11)：62-69.

[12]胡昌寿，周正伐，周炽九.航天可靠性设计手册[M].北京：机械工业出版社,1999.

(责任编辑杨继森)