泡沫铝板弯曲振动特性数值研究

王鹏飞，刘孟周，刘同辉，张成立

（北京卫星环境工程研究所，北京 100094）

0 引言

泡沫铝是以氢化钛为黏接剂和发泡剂，加入到纯度为99.85%的熔融铝中搅拌而制成的，是近年发展起来的一种集结构、性能一体化的新型功能材 料[1-3]。作为结构材料，泡沫铝具有轻质、高强度的结构特点[4-5]。泡沫铝还具有优异的物理性能、化学性能和机械加工性能，如密度小、吸收冲击能力强、防火性强、抗腐蚀、隔音降噪、导热率低、电磁屏蔽性高、有过滤能力、易加工、成形精度高、可进行表面涂装。目前泡沫铝板材已广泛应用于航天器缓冲结构、环境控制系统、热控系统、光学系统以及相关总装领域[6-8]。

弯曲变形是泡沫铝材料最常见的变形方式之一，然而对泡沫铝弯曲振动的研究较少。总装设计过程中要求所有外部工装设备均需远离舱体自身固有频率，而舱体的频率通常仅为个位数量级甚至更小。因此，有必要开展对泡沫铝的弯曲振动特性的研究。

本文基于泡沫铝的实际使用状态，建立其弯曲振动理论模型和有限元模型，进行求解和对比分析，重点关注泡沫铝的弯曲振动特性，以研究不同材料参数对其弯曲振动频率及变形的影响。

1 弯曲振动特性分析

本文针对载人航天器舱内使用的泡沫铝板，以Timoshenko梁理论为基础，推导泡沫铝板弯曲振动理论模型。同时利用ANSYS仿真软件建立泡沫铝板的有限元模型。通过对两个模型的求解，获得模态频率，并进行对比分析。

1.1 结构参数

泡沫铝的功能特性主要由金属骨架的孔隙特征决定，包括孔的类型、孔径、孔隙率等。不同孔隙率的泡沫铝会有不同的结构参数，本文选取孔隙率为80%的泡沫铝板进行分析，相关材料参数如表1所示[9]。

表1 泡沫铝材料参数 Table1 Materials parameters of aluminum foam

1.2 振动理论模型

泡沫铝板宽度与长度之比并不是小值，选择以Timoshenko梁理论为基础建立弯曲振动理论模型，为了使模型更加准确，应考虑剪切变形和转动惯量对泡沫铝板弯曲振动产生的影响[10-11]。

如图1所示，取微段dz作为研究对象。图中的虚线为忽略剪切变形的情况。当考虑微段dz剪切变形时，Timoshenko梁截面法线与梁轴线的切线将不再重合，即发生了由切应力引起的横截面错动（实线与虚线的位置变化），使得横截面内各点之间存在相对位移，因此在横截面内切应力不是恒定不变的。为简化计算，取横截面内的平均切应力为等效切应力[12]。

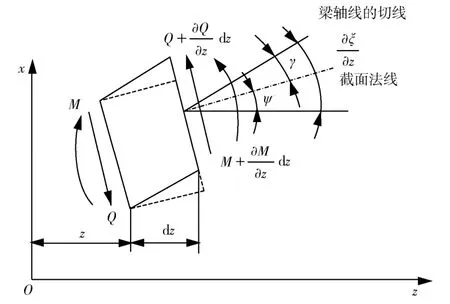
图1 Timoshenko 梁及剪切变形 Fig.1 Timoshenko beam and shear distortion

根据材料力学与弹性力学的知识，若分别用ξ,η,ζ表示微体积元沿x,y,z轴的位移，可以得到应变分量表达式为

式中：S3和S5分别对应z轴截面的轴向应变与切应变；ψ为弯矩引起的截面转角，以逆时针旋转为正；s33和s55分别对应材料弹性模量和切模量的倒数；T3和T5分别对应z轴截面的轴向应力与切应力。

针对Timoshenko梁受力图，建立力和力矩平衡方程，忽略其中高阶无穷小量，得到弯曲变形过程中振动微分方程组为

式中：ρ为密度，kg/m3；A为截面面积，A=B×D，m2；Ⅰ为截面惯性矩，Ⅰ=B×D3/12，m4；κ为截面形状系数，矩形截面κ=0.833。

在简谐振动激励下，假设振型函数ξ=ξ(z)· ej(ωt+ϕ)，转角函数ψ=ψ(z)ej(ωt+ϕ)，其中ω= 2πf，f表示泡沫铝板的模态频率。

将假设振型函数和转角函数代入式(2)，令α=ρs55/κ+ρs33，β=ρAs33ω2/Ⅰ-ρ2s33s55ω4/κ，得到不含 时间分量的振型函数ξ(z)、转角函数ψ(z)、弯矩函数M(z)和剪力函数Q(z)的表达式为

式中：C1,D1,C2和D2为各函数项的常数系数；m为简化计算引入的参数，m=ρs55ω2/κ；1=nⅠ0和A0分别为截面惯性矩（m4）与截面面积（m2）。

1.3 频率求解

将泡沫铝板等效为两端自由的复合梁结构，由振动边界条件建立弯曲振动力学平衡条件，如表2所示，表中L表示泡沫铝板的长度。

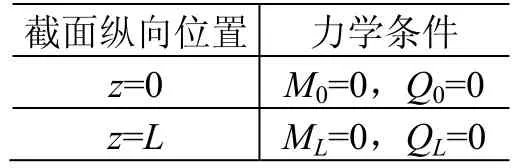
表2 自由振动边界条件 Table2 Boundary conditions of free vibration

根据表2中的边界条件及连续条件建立矩阵形式的齐次方程组，记P×C=0，其中：P为系数矩阵，C为振型函数的常数系数矩阵，即

通过求解上述齐次方程组就可以得到泡沫铝板弯曲振动的频率。理论上，使矩阵P行列式的值等于0 时的频率就是泡沫铝板的模态频率。本文利用MATLAB 软件编程，对P行列式的值进行扫描。在扫描过程中，当行列式的值发生正负符号变化时，就获得了模态频率。

P是关于振动频率的奇异矩阵，只能求解出振动方程中各个常数系数之间的相互关系，无法解算出各个常数系数的数值。实际上，在求解振动方程的过程中有一个条件可用来求解振动频率。考虑到泡沫铝的弯曲刚度较大，是小变形问题，因此，在求解过程中假设C11=0.001。去除上述齐次方程组中任意一行，取剩余的组成方程组，代入C11和振动频率，就可以获得除C11以外的其余所有常数系数，进而获得泡沫铝板弯曲振动的振型函数ξ(z)、转角函数ψ(z)、弯矩函数M(z)和剪力函数Q(z)。泡沫铝板弯曲振动的振型曲线及振动频率如图2～ 图4所示。为了与上述计算结果对比，利用ANSYS 建立泡沫铝板弯曲振动的有限元模型。通过对有限元模型的模态分析，获得模态频率和振型曲线。表3为泡沫铝板理论模型的解析结果与有限元模 型的仿真结果对比；图5～7 为泡沫铝板有限元模型经前三阶模态分析后提取的振型曲线。

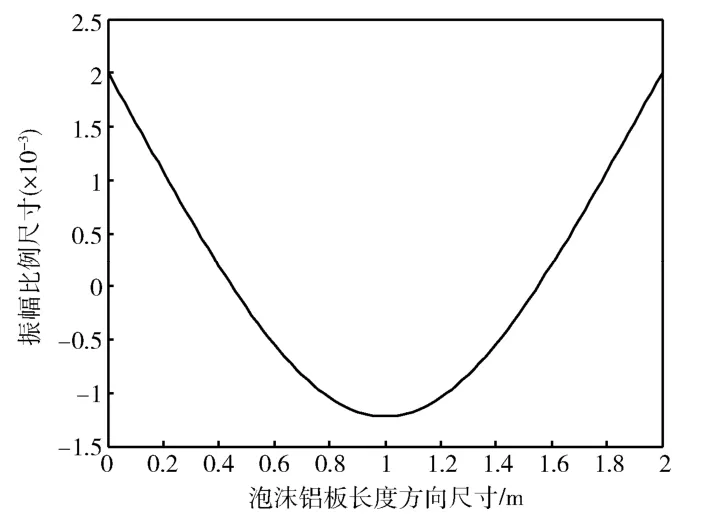
图2 一阶弯曲振型（f = 56.023 Hz） Fig.2 First-order bending mode(f = 56.023 Hz)

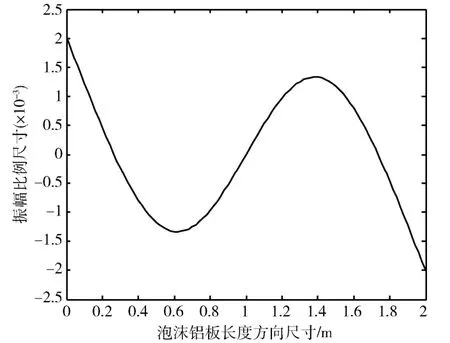
图3 二阶弯曲振型（f = 153.425 Hz） Fig.3 Second-order bending mode(f = 153.425 Hz)

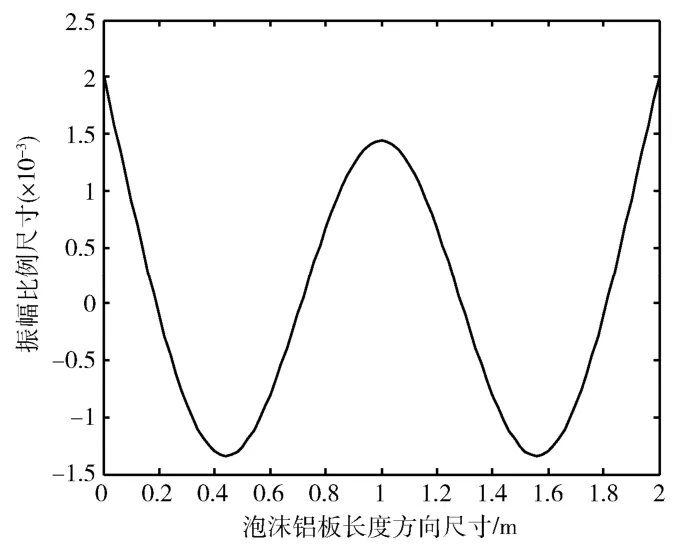
图4 三阶弯曲振型（f = 298.893 Hz） Fig.4 Third-order bending mode(f = 298.893 Hz)

表3 理论模型与有限元模型结果对比 Table3 Result comparison between analytical model and FEA model

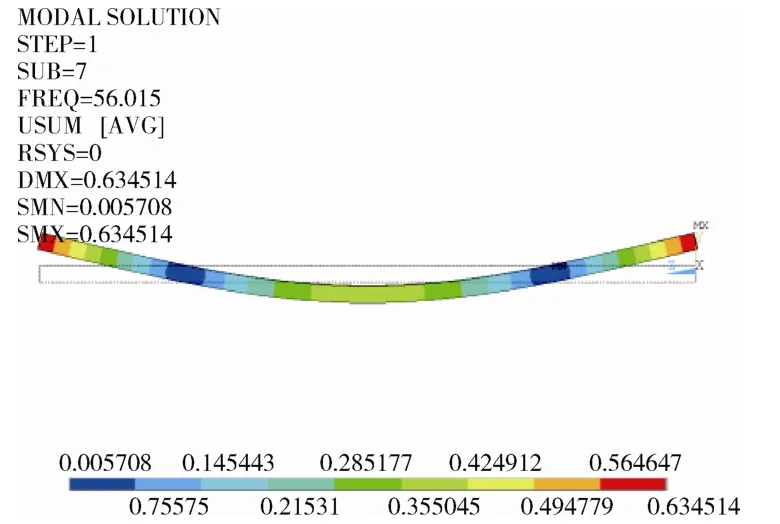
图5 一阶弯曲振型（f = 56.015Hz） Fig.5 First-order bending mode(f=56.015 Hz)

图6 二阶弯曲振型（f =154.490 Hz） Fig.6 Second-order bending mode(f=154.490 Hz)

图7 三阶弯曲振型（f=302.288 Hz） Fig.7 Third-order bending mode(f=302.288 Hz)

对比分析理论模型和有限元模型的模态频率，可看出结果十分接近，频率相差最大的三阶弯曲振动也仅为1.12%。通过有限元分析验证了泡沫铝板弯曲振动理论模型的正确性，可用于分析泡沫铝板材料参数对频率的影响。

对弯曲振动理论模型求解，得到了泡沫铝板弯曲振动的基频为56 Hz 左右，远大于舱体的基频，完全满足总装技术要求。

2 材料参数对弯曲振动的影响

在制作过程中，可以通过改变材料参数以得到不同弯曲振动频率的泡沫铝板。本节利用前述理论模型，研究不同的材料弹性模量和密度（其他参数不变）对泡沫铝板弯曲振动频率的影响。

2.1 弹性模量对振动频率的影响

分析过程中仅改变弹性模量，而其他参数保持不变（泡沫铝材料参数见表1）。弹性模量对振动频率的影响如图8所示。

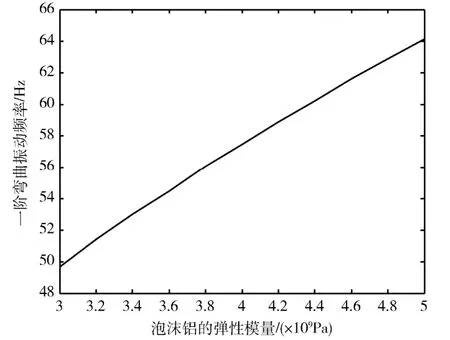
图8 弹性模量对振动频率的影响 Fig.8 Influence of elastic modulus on the vibration frequency

2.2 密度对振动频率的影响

仅改变材料密度，其他参数保持不变（泡沫铝材料参数见表1）。密度对振动频率的影响如图9所示。

图9 密度对振动频率的影响 Fig.9 Influence of density on the vibration frequency

2.3 小结

本节通过理论模型分析了泡沫铝材料参数对弯曲振动的影响，可以看出，随着弹性模量的增加，泡沫铝板的振动频率随之增加；随着密度的增加，振动频率逐渐变小。同时通过理论求解可知，在忽略结构阻尼自由弯曲振动情况下，随着泡沫铝材料参数的改变，振动过程中的最大变形变化较小，但在工程应用中最大变形还与材料的结构阻尼及相应外力作用有关。

综上所述，可以通过改变材料参数来获得不同的泡沫铝的振动频率，进而可以根据该频率选择其具体适用环境。

3 结束语

本文利用泡沫铝板的弯曲振动的理论模型和有限元模型开展了对比研究，验证了弯曲振动理论模型的有效性。同时利用理论模型开展了不同材料参数对泡沫铝弯曲振动频率的影响。研究结果可用于指导泡沫铝在总装设计过程中的弯曲变形分析，以及不同的总装工况下对泡沫铝结构参数的合理选择。后续将继续开展泡沫铝板材料的试验研究，详细分析泡沫铝板材料的弯曲特性。

（References）

[1] 刘培生.多孔材料引论[M].北京: 清华大学出版社,2012: 3-8

[2] Koerner C,Ties M,Singe R F.Modeling of metal foaming with lattice Boltzmann automata[J].Adv Eng Mater,2002,4(10): 765-769

[3] 陈雯,刘中华,朱诚意,等.泡沫金属材料的特性、用途及制备方法[J].有色矿冶,1999,30(1): 33-36 Chen Wen,Liu Zhonghua,Zhu Chengyi,et al.The characteristics,use and preparation method of foam metal materials[J].Non-ferrous Mining and Metallurgy,1999,30(1): 33-36

[4] 陈祥,李言祥.金属泡沫材料研究进展[J].材料导报,2005,17(5): 5-11 Chen Xiang,Li Yanxiang.Porous metals: research advances and applications[J].Materials Review,2005,17(5): 5-11

[5] 左孝青,杨晓源,李成华.多孔泡沫金属的研究进展[J].昆明理工大学学报,1997,22(1): 90-93 Zuo Xiaoqing,Yang Xiaoyuan,Li Chenghua.Developments of research work on foamed metal[J].Journal of Kunming University of Science and Technology,1997,22(1): 90-93

[6] 杨振海,罗丽芬.泡沫铝技术的国内外进展[J].轻金属,2004(6): 3-6 Yang Zhenhai,Luo Lifen.Review and prospect of foamed aluminum in China and other countries[J].Light Metals,2004(6): 3-6

[7] 田杰,胡时胜.基体性能对泡沫铝力学行为的影响[J].工程力学,2006,23(8): 168-171 Tian Jie,Hu Shisheng.Effect of matrix properties on the mechanical behaviors of aluminum foams[J].Engineering Mechanics,2006,23(8): 168-171

[8] Duarte I,Mascarenhas J,Ferreira A,et al.The evolution of morphology and kinetics during the foaming process of aluminium foams[J].Key Eng Mater,2002,24(8): 96-101

[9] 安郁熙.泡沫铝消声器性能分析与实验研究[D].山东: 山东科技大学,2009: 26

[10] Timoshenko S.Vibration problems in engineering[M].New York: D Van Nostrand Company,1937: 337-338

[11] Taskin V,Ece M C,Aydogdu M.Vibration of a variable cross-section beam[J].Mechanics Research Communications,2007,34(1): 78-84

[12] Zhang Qiang,Shi Shengjun,Chen Weishan.Study on analytical modeling of sandwich type piezoelectric transducer using bending vibration mode[C]∥2012 9thIEEE International Conference on Mechatronics and Automation.Chengdu,China ,2012: 926-930