卫星外露电缆束介质结构深层充电仿真分析

王 松，武占成，唐小金，易 忠

（1.军械工程学院 静电与电磁防护研究所，石家庄 050003； 2.北京卫星环境工程研究所，北京 100094）

0 引言

空间高能带电粒子可穿透卫星蒙皮并沉积到内部介质或孤立导体内，经过电荷输运并建立电场，容易引发卫星内部充电效应[1]。卫星蒙皮和设 备机箱的屏蔽层可以有效保护内部工作电路免受高能带电粒子的影响。根据NASA-HDBK-4002A给出的防护建议，对于GEO 卫星，厚度达到2.8 mm的铝屏蔽层可以有效缓解内部充电效应。然而，卫星蒙皮外侧同样存在相当数量的介质材料，这些材料直接遭遇空间高能带电粒子冲击，同样产生内部电荷积累[2]，一旦发生放电，很可能将脉冲干扰经电缆耦合进入星内关键工作部件；当相邻介质电位差超过一定值时，还可能诱发邻近太阳电池板的大面积对空间放电[3]。因此，对外露电缆束中的绝缘层介质深层充电效应须给予足够重视。

近十几年空间介质充放电效应研究取得了一些进展[2,4-5]，理论分析和数值仿真依然是评估介质深层充电程度及其放电风险的主要工具。欧洲航天局编制了专门软件DICTAT[6]，但只限于对平板和圆柱等简单几何结构的介质进行内带电仿真。为了精细化建模和分析不同结构，深层充电的三维仿真随之兴起[7-8]。前期研究中，对星内典型电路板内带电情况进行了三维建模仿真[9]，发现三维仿真可以更准确地评估介质充放电风险。中科院空间中心研究人员对星内电缆网内部充电效应进行三维仿真分析，考察了单根电缆在直立、弯曲和不同接地情况下的带电结果，指出星内固定电缆装置需避免大尺寸（厘米级）的介质材料[10]。

本文基于粒子输运的蒙特卡罗模拟和介质充电的电流连续性方程，侧重于对外露电缆束的交叠介质结构的深层充电进行三维仿真分析，为星用外露电缆束的科学安装及使用提供参考。

1 介质深层充电理论与模型

1.1 理论建模

高能带电粒子是导致介质深层充电的电流源。因为介质的极低电导率，入射电荷可以在介质内沉积并形成空间分布。与此同时，不能忽略介质存在一定的电导率，尤其受高能粒子辐射导致的辐射诱导电导率，对介质沉积电荷的有效泄放发挥着重要作用。仿真中，当介质接收到来自空间高能粒子流的电荷与介质自身泄放电荷数量相等时，认为介质深层充电达到平衡状态，此时对应最高充电电位和局部最大电场强度。

首先从高斯定理和电荷守恒定律推出介质内电流密度连续性方程。由高斯定理

和电荷守恒定律

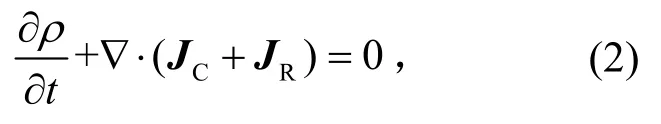
联立得到电流密度连续性方程为

式中：D为介质内电位移矢量，对于各向同性线性介质，其与电场强度E存在关系D=ε0εrE；ρ为介质电荷密度；JC和JR分别代表介质内传导电流密度和高能带电粒子入射对应的外部电流密度。式(3)括号中的3 项之和代表介质内总电流密度。

然后，已知介质相对介电常数εr、电导率σ和JR，结合一定的边界条件，应用欧姆定律JC=σE和电场强度与电位的关系式

可以求得介质内电场强度与电位的时空分布。

1.2 电导率与入射电流密度的求解

电导率是决定介质深层充电的关键参数，一般需要综合考虑温度、电场强度和辐射剂量率对电导率的影响，尤其是辐射剂量率，其对应的辐射诱导电导率往往能起主导作用。

将电导率分成2 部分，

式中：σric为辐射诱导电导率；σET为温度和电场共同作用下的电导率。

根据Fowler 公式[11]，σric依赖于靶材料的辐射剂量率D˙，并满足关系式

式中：kp是由介质材料物理性质决定的常数；=dD/dt是辐射剂量率（D是辐射剂量）；参量α代表介质内俘获能级分布情况，0.5＜α＜1.0。

另外，温度和电场强度对介质载流子浓度和迁移率产生影响。电导率随温度的变化满足

因为本文模型具有典型的多约束非线性混合规划特性，所以基于现有相关算法的优缺点，设计了一种改良模拟退火遗传混合算法(Improved Simulated Annealing Genetic Algorithm, ISAGA)，首先利用改进的遗传算法全局搜索确定最优解区域，再改进模拟退火算法区域搜索寻优解，以提升模型求解的效率与精度。

式中：A为由介质材料物理性质决定的常数；k为玻耳兹曼常数；EA为材料的电导激活能；T为温度，K。同时考虑强电场效应，得到经验公式[12]

式中：E为电场强度模值；βF=(e3/πε)0.5，取决于材 料的介电常数ε；e为电子电量；δ为电子在介质晶格间的跳跃距离，一般取值1 nm[13]。

辐射剂量率D˙和带电粒子入射对应的电流密度RJ均需要借助专门的粒子输运模拟软件Geant4进行计算。Geant4 是一款开源的免费软件，且经过多年更新，其计算准度与精度已经得到广泛认可。首先根据材料的元素组成与质量密度，由Geant4计算空间分布的沉积电荷与吸收剂量，然后经过换算得到一定的空间电子通量下对应的和空间电流密度Qj。将∇·JR=-Qj代入式(3)可消去RJ。详细换算过程参见文献[14]。

综上，得到介质深层充电的数学模型：

已知Qj和相关参数，根据不同的边界条件可求得介质内的电场强度与电位的时空分布。

2 外露电缆束及其模型提取

卫星蒙皮外存在多根成捆电缆束。如图1(a)所示，将电缆捆束的横截面视为正六面体形状，单根电缆的外径为2.08 mm，内径为1.70mm，绝缘层材料为聚四氟乙烯，内芯导体材料是铜。导体芯与卫星整体设备保持电气连接，故将其视为接地。

图1 电缆束示意图及其Geant4 电荷输运仿真图示 Fig.1 Sketch of the electric cable bundle and its illustration in Geant4 simulation

3 仿真结果与分析

3.1 沉积电荷与电导率

设置材料属性，聚四氟乙烯对应的介电常数εr=2.15；当T=293.15 K 时，电导率σT=1×10-16S/m；kp=2.0×10-12kg·s·J-1·Ω-1·m-1，α=0.7（量纲1 的指数），EA=1 eV=1.6×10-19J，δ=10-9m。以图1(a)沿x轴正方向最右侧的介质材料薄层为代表，其厚度为0.19 mm，得到沿径向厚度方向的辐射诱导电导率σric分布如图2实线所示，沉积电流的空间密度Qj如图2虚线所示。图中x= 5.105 mm 代表介质层最外侧。总体上看，越靠近最外层离辐射源越近，故沉积电荷密度和吸收剂量越大，从而换算得到的Qj和σric也随之变大。其中Qj在靠近内侧表面位置有所增大，这主要是受导体芯线的影响。具体来讲，在入射过程中，当电子碰到密度比绝缘层介质密度大的导体时，会出现显著的散射效应，散射回介质内的电子的再次沉积导致Qj在靠近内侧表面位置有所增大。

图2 沿厚度方向的辐射诱导电导率与空间电流密度 Fig.2 σric and Qj along the direction of thickness

3.2 充电电位与电场强度

首先讨论7 根与19 根电缆束的情况。因为电缆束一般很长，其电场强度和电位沿长度方向的变化基本可以忽略，故可以截取厚度仅为0.2 mm 的薄层进行对比分析。

借助Comsol Multiphysics 仿真平台，对式(9)进行求解，得到平衡状态下的电缆束充电电位与电场强度，其中参量Qj和σric的取值如前所述。

如图3所示，根数不同时电缆束的充电电位分布与峰值基本相同，峰值在-20 V 量级，基本不存在放电风险。这主要是因为导线绝缘层厚度只有0.19 mm，而深层充电导致的表面电位随介质厚度增加显著增大[10]。

图3 不同根数电缆束的电位分布对比 Fig.3 Comparison of potential for two cases of 19-core and 7-core wire bundles

另外，二者充电最高电场强度也十分接近，约为2.0×105V·m-1。这里以7 根电缆束为例，画出电场强度分布如图4所示。值得注意的是，电场强度在靠近接地侧过程中逐渐增大，在最外圈介质的接地侧达到峰值。而由于电缆金属芯线的屏蔽作用，被遮挡的介质层的电位和场强均很小，故19 根电缆束的电场强度分布与此类似。

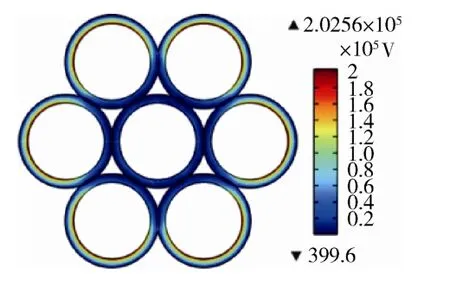
图4 充电平衡状态电场强度分布 Fig.4 Distribution of E-field under balanced condition

以图1(a)中两点A(5.105,0)和B(0,4.560)为参考，经过时域仿真计算，得到两点充电电位随时间的变化过程如图5所示。

图5 充电电位时域特征 Fig.5 Time domain variation of the charging potential

可以看出，充电时间常数约为300 s，A点平衡电位稍高。这主要是因为从横截面来看，A点处在顶点位置，对应的电荷沉积比B点稍大，虽然A点的辐射剂量率（决定了σric）同样比B点稍大，但因为指数α=0.7＜1 的作用，使得增大电荷沉积率对提高电位的贡献较降低σric更加明显，因此A点平衡电位稍高。

实际应用中，电缆束需要用外部构件捆绑在一起，在局部捆绑不力的地方会出现松动，即多根电缆之间相互分离。分别建立模型，考察电缆相互分离情况下的充电特性，如图6(a)所示；以及分析捆绑介质块对充电的影响，如图6(b)和(c)所示，其中介质块厚度分别为0.4 mm 和0.8 mm。从图6(a)与图3(a)对比看出，电缆束中各个导线绝缘层是否紧密邻接对介质深层充电的峰值电位影响不大，然而由于外圈电缆之间出现缝隙，使电子得以穿过并沉积到内圈介质层中，这增大了相邻线缆之间因为不等量充电导致放电的发生概率。存在捆绑介质块时，得到的充电电位（与电场强度）显著增大，与星内介质的充电规律是一致的[10]，且电位峰值随介质块厚度增加而升高，介质块厚度从0.4 mm 增大到0.8 mm 时，峰值电位从-512 V 升高到-873 V，电场强度峰值从2.3×106V·m-1升高至4.0×106V·m-1。考虑航天器表面的不等量充电效应，该电位很有可能引发相邻结构之间静电放电，而且该量级电场强度有可能导致绝缘材料击穿放电。

图6 19 根电缆束在分离状态与存在捆绑介质情况下 的电位分布 Fig.6 Potential distribution in 19-core wire bundle under separated and bonded-up condition

4 结束语

本文采用Geant4 粒子输运模拟与基于电荷守恒的介质深层充电模型，对卫星外露电缆束介质结构的深层充电进行时域三维仿真分析。结果表明，在GEO恶劣电子环境下，绝缘介质层厚度为0.19 mm的电缆束基本不存在深层充电导致的击穿放电风险，电缆束的分离状态与紧密邻接状态的充电电位峰值基本相同，但电位和电场强度分布存在差异：分离状态下内部电缆之间存在不等量充电，增大了发生放电的风险；捆绑电缆的绝缘介质块是充放电风险较大的区域，当其厚度达到0.8 mm 时，充电电位接近-103V 量级，电场强度峰值可到4×106V·m-1，且放电风险随着介质块的厚度增加而增大，需要给予特别关注。

（References）

[1] Wrenn G L.Conclusive evidence for internal dielectric charging anomalies on geosynchronous communications spacecraft[J].Journal of Spacecraft and Rockets,1995,32(3): 514-520

[2] 黄建国,陈东.卫星中介质深层充电特征研究[J].物理学报,2004,53(3): 961-966 Huang Jianguo,Chen Dong.A study of characteristics for deep dielectric charging on satellites[J].Acta Physica Sinica,2004,53(3): 961-966

[3] Hoang B,Wong F K,Corey R L,et al.Combined space environmental exposure test of multijunction gaas/ge solar array coupons[J].IEEE Transactions on Plasma Science,2012,40(2): 324-332

[4] 乌江,康亚丽,张振军,等.两种典型星用聚合物介质抗内带电改性防护技术研究[J].真空与低温,2012,18(1): 26-32 Wu Jiang,Kang Yali,Zhang Zhenjun,et al.Study on the deep dielectiuc charging protection technology of two typical polymers on spacecraft[J].Vacuum and Cryogenics,2012,18(1): 26-32

[5] Frederickson A R,Benson C E,Bockman J F.Measurement of charge storage and leakage in polyimides[J].Nuclear Instruments and Methods Physics Research B,2003,208(1): 454-460

[6] Sorensen J D,Rodgers J.ESA’s tools for internal charging[J].IEEE Transactions on Nuclear Science,2000,47(3): 491-497

[7] Katz I,Kim W.A 3-D model of circuit board internal electrostatic charging[C]//11thSpacecraft Charging Technol Conf Albuquerque,NM,2010

[8] Sarrailh P,Garrigues L,Hagelaar G,et al.Three-dimensional model of internal charging using SPIS[C]//12thSpacecraft Charging Technol Conf.Kitakyushu,Japan,2012

[9] Tang X J,Yi Z,Meng L F,et al.3-D internal charging simulation on typical printed circuit board[J].IEEE Transactions on Plasma Science,2013,41(12): 3448-3452

[10] 孙建军,张振龙,梁伟,等.卫星电缆网内部充电效应仿真分析[J].航天器环境工程,2014,31(2): 173-177 Sun Jianjun,Zhan Zhenlong,Liang Wei,et al.Simulation of internal charging for electric cables used in the satellite[J].Spacecraft Environment Engineering,2014,31(2): 173-177

[11] Fowler J F.X-ray induced conductivity in insulating materials[C]//Proceedings of the Royal Society of London,Series A: Mathematical and Physical Sciences,1956,236: 464-480

[12] Adamec V,Calderwood J H.Electrical conduction in dielectrics at high fields[J].Journal of Physics D: Applied Physics,1975,8(5): 551-560

[13] Rodgers D J,Ryden K A,Wrenn G L,et al.An engineering tool for the prediction of internal dielectric charging,AFRL-VS-TR-20001578[R],2000

[14] 王松,易忠,唐小金,等.地球同步轨道外露介质深层带电仿真分析[J].高电压技术,2015,41(2): 687-692 Wang Song,Yi Zhong,Tang Xiaojin,et al.Analysis of exposed dielectric internal charging in GEO via numerical simulation[J].High Voltage Engineering,2015,41(2): 687-692

[15] Rodgers D J,Ryden K A,Latham P M,et al.Engineering tools for internal charging: final report,ESA contract 12115/96/NL/JG(SC)[R],1998