B2C电子商务竞争结构及发展演化规律

李 杰，王宇菲，王 聪，张志颖

一、B2C的发展历程与现状

2013年，我国B2C 电子商务市场的竞争格局变得越来越清晰，从之前多个企业均衡较量的混乱局面，逐渐形成梯队化的明朗格局。这一市场竞争格局的形成标志着我国B2C电子商务市场走向了成熟。

在世界B2C电子商务体系中，发展较早且相对成熟的国家是美国，始于1994年，到目前为止已有20年的发展历程。我国的发展起步相对较晚，1999年成立了第一家B2C电子商务企业——当当网，到目前已有15年的发展历史。2000年我国B2C电子商务交易额为3.9亿元人民币，国内B2C网站有677家，有一定影响并且连续在运营的只有205家。到2013年，B2C电子商务交易额已增长到6 500亿元，网络零售企业数已经达到29 303家。在短短的十几年间，我国B2C电子商务市场飞速发展。根据《1997-2009：中国电子商务十二年调查报告》所述，我国的电子商务服务企业经历了从萌芽到转型与升级的五个阶段，其中2006年标志其开始进入高速时期。在此之后，国际国内知名的电子商务企业不断成长，电子商务的配套服务设施，如物流、支付、信用和其他基础环境逐步改善，加之我国企业和网民对电子商务的认识越来越成熟和理性，人们的消费行为发生了重大改变。随着消费者参与度的提高，电商之间的竞争也日趋激烈。

在我国电子商务零售市场中，主要以B2C和C2C为主。从整个电子商务零售市场来看，B2C的发展最为迅速，尤其是近几年进入者增速较快，随之退出市场的速度也较快，一些规模较大、实力较强的网站竞争力愈来愈强，例如天猫、京东等。与之区别较大的是C2C，尽管一直有新进入者努力尝试，但是目前C2C市场仍然是以淘宝独大的局面。根据《2013年度中国电子商务市场数据监测报告》，淘宝的市场份额占到了96.5%，表明C2C市场的竞争很不充分。根据目前我国电子商务市场的发展状况来看，B2C市场的竞争更加激烈、充分，且受到规模不断增长的用户的影响更大。

我国B2C市场发展迅猛，中国电子商务研究中心截止到2013年12月份的数据显示，我国网络零售市场交易规模已达到18 851亿元，与2012年相比，增长了42.8%，在社会消费品零售总额的占比达到了8.04%，同比增长了27.6%。在中国2013年B2C市场交易份额排名的前十中，天猫仍然以50.1%市场份额排名第一，京东、苏宁易购分别位于第二、第三。与2012年B2C市场的交易份额相比，前四位的企业没有发生明显变化，而新蛋网则首次从行业前十中消失。2013年中国B2C市场的特征表现为平台的开放，由于自营商品的销售普遍出现亏损，各大电商纷纷开放第三方平台，以实现其业务和交易额的快速增长。

基于我国电子商务市场的这种局面，以及B2C市场较强的环境适应性，随着亚马逊进入中国、阿里巴巴开拓国际市场、兰亭集势赴美上市等等，电子商务的发展越来越全球化，并且由于美国电子商务起步较早，市场相对成熟，因此本文选取中国和美国的B2C电子商务市场作为研究对象，分析它们各自市场竞争结构的特征以及它们之间的异同。

二、电子商务研究现状及幂定律的应用

国内外学者在电子商务方面的研究主要从应用、技术、支持和实施以及其他四个方面开展工作。在应用方面主要是包括各类电子商务系统，如零售业的电子商务系统、金融电子商务系统、教育等门户网站以及最近几年流行的移动电子商务系统。技术方面主要包括网络安全、前台后台的支持系统、网站布局设计和算法等。支持和实施则是包括电子商务的环境、相关政策和企业战略等方面。其余的一部分研究则归类到其他，例如一些结合具体企业的案例研究或者是针对影响电子商务发展的某一方面的因素研究等。王渊（2008）等人选取了169篇电子商务相关文献进行研究，基于主题统计，样本显示的结果支持上述的四个研究方面。李杰（2008）对2000-2006年中文核心期刊发表的4 808篇电子商务相关文献进行分类分析，我国电子商务研究主题按论文数量排序依次是技术、市场、支持和应用。

回顾电子商务分类模型的研究文献可知，电子商务研究的主要方面在于企业层，即微观运作层，宏观上的研究很少，尤其是电子商务市场竞争结构演化规律的研究目前没有见到。宏观研究的意义十分重要，它能够揭示电子商务市场的竞争结构特征和动态变化规律。竞争结构特征用于新进入企业把握电子商务市场的竞争结构格局和竞争形势，分析自己企业进入市场后所面临的竞争压力，决定是否进入以及进入后的竞争战略。动态变化规律揭示市场的发展规律，是趋于垄断还是趋于更加竞争，便于新企业选择进入一个比较成熟但垄断的电子商务市场，还是开拓性进入一个新市场。因此，本文将从宏观层面研究电子商务市场的竞争结构及其动态变化规律。

现有研究发现，很多市场经济现象的背后都符合幂定律。根据幂定律，本文猜想电子商务市场竞争结构应该符合幂定律。以y为因变量，x为自变量所形成的函数关系y=cx-a就称为幂律分布。其中x代表统计量从高到低的排名，y代表排名所对应的统计量。在幂律分布的发展过程中做出突出贡献的是Zipf和Pareto（胡海波，2005）。1932年，哈佛大学语言学家Zipf在研究文本中单词出现的频率时发现了这种分布。他将单词在文本中出现的频率由高至低排列，发现每个单词出现的频率和它的名词存在反比的关系，即y=cx-a，人们将这一关系式称为Zipf定律。1877年，意大利经济学家Pareto在针对人们财富的调查取样中发现大部分的财富流向了少数人手里；同时，他还发现某一个族群占总人口数的百分比和他们享有的收入之间也存在着一种关系。他从大量事实中发现社会上20%的人占有80%的社会财富，即在社会中财富的分配是不平衡的。在生活中还存在许多与之相类似的不平衡现象，人们把这种不平衡的关系统称为二八定律即Pareto定律。

在自然界与社会生活中，科学家们普遍感兴趣的事情基本都有一个典型的规模，而个体的尺度在这一特征尺度附近变化很小。比如学生的成绩，在某次考试中绝大多数学生的成绩都集中在平均值附近，很少会出现集中在高分和低分的情况。如果以成绩为横坐标，以成绩所对应的人数为纵坐标，可绘制出一条曲线，该曲线两边下降得极快。这种用平均值来表征整个群体特征的分布称之为泊松分布。然而对于其他一些分布，例如个人收入或一些金融数据的分布，就与泊松分布大不一样了，个体的情况可以在很大的范围内波动，这一波动经常可以跨越几个数量级。幂律分布是与泊松分布显著不同的另一分布，广泛存在于众多领域中，例如物理学、金融学、计算机科学以及社会科学，且表现形式各不相同。尤其是目前许多领域的发展都面临着一些复杂系统问题。而这一分布很好的表征了复杂网络中的无标度特性，即个体值的波动范围相当大。根据这一特性，本文认为激烈的B2C电子商务市场竞争是一个复杂的网络，也应该会表征出无标度的特性，即幂律分布的特征。

随着计算机和数学工具的迅猛发展，学者们对金融数据的研究变得相对容易。这一研究促使了经济物理学的诞生，例如Kadanoff（1971）和Montroll（1974）等。之后该领域吸引了越来越多的学者，模型的变化和改进多种多样，所涉及的数据范围也越来越宽泛。Adrian（2001）对美国和英国的财富和收入分布进行研究，证实其尾部符合幂律分布规律。Anders（2008）研究发现在阿根廷、巴西、智利、墨西哥、秘鲁、委内瑞拉、中国香港、印度尼西亚、韩国、马来西亚、菲律宾和泰国等多个国家和地区的股票市场中，幂律分布规律很好地描述了存在于新兴市场中的投机泡沫。张宇（2004）等人介绍了有关金融资产收益率分布呈现幂律特征的主要研究方法和结果，以及与其相关的理论解释。高建敏（2007）根据《福布斯》公布的中国大陆富人榜排名，以排名为横坐标，他们所拥有的财富为纵坐标，可绘制出一条向右偏斜的、拖着很长尾巴的分布曲线，这与泊松分布曲线有着明显的不同，称之为幂律分布。这种分布表明，大部分的财富主要集中在少数人手中，即符合著名的Pareto定律。司马则茜(2009)等人收集国内外公开的中国银行系统操作损失数据，在此基础上，运用分形的POT幂律模型对其进行了估算，表明了操作存在的严重风险。吉翔（2012）使用对数周期性幂律模型对我国股市的泡沫进行了分时间段研究，证实我国股市具有分形特征，存在符合幂律分布规律的泡沫现象。

除了经济学、物理学领域的研究之外，其他基于幂律分布的研究也是层出不穷。在互联网领域，幂律分布更是无处不在，从网上信息量的分布、站点拥有的网页再到个人的搜索行为几乎都存在幂律分布。在互联网这个看似混沌复杂的领域，却出乎意料地存在着极强的规律性。学者们把在互联网中存在的幂律称为“富者益富”，这一机制与西蒙模型的“成功产生成功”是一致的。山石、邱红（2008）在文献中指出，当出现一个新的网页或一个新的链接时，它会以一定的概率链接到已有的节点，而这一概率与所有站点拥有的链接量存在相关关系，站点拥有的链接量越大，新链接接入的可能性越大，依据这一过程，最终就形成了链接量在网站中的幂律分布。近年来，学者们经过研究发现在人口统计学中幂律分布现象同样存在。施华萍（2009）在研究我国人口分布的过程中发现省、市、县三级人口的分布具有相似的幂律分布规律，并采用无标度网络上的聚集体迁移模型很好地解释了我国人口分布的演化规律。Aaron Clauset（2009）等人改变前人应用最小二乘法来分析具有幂律分布规律的数据，而选用了最大似然估计法来对数据进行处理，并用这种方法在24个不同学科的现实数据中得到了验证。杨波（2007）等人也基于这种方法并引入KS检验统计量和欧几里得距离来检验了这种方法的估计效果，最后通过CNN模型网络和爵士音乐家网络两个实例验证了新方法较图形方法更好的估计效果。刘臣（2013）研究中国重要中文期刊文献之间相互引用的关系时，证明了中国学科知识网络的边权分布具有幂律分布特征。

目前，在电子商务领域基于幂律分布规律的研究还较少，且主要以基本概念的描述和某些行为的局部特征研究为主，对其宏观层面——市场竞争结构全局特征的理性认识或者定量研究还有很多欠缺。俞宣伊（2010）基于复杂网络以淘宝网为例对C2C电子商务交易网络的演化机制和动态特征进行了分析，发现了 C2C交易网络的度分布遵循幂律分布，这说明C2C交易网络的演化满足优先连接和增长定律。叶作亮（2011）基于幂律分布对C2C顾客的购买行为特征进行了研究，发现在C2C电子商务的环境下，顾客的购买行为呈现出长尾分布的特征。他进一步构建模型，解释了形成这一规律的内在机制。高瑞泽（2012）从生态群落的角度研究了电子商务群落之间的竞争关系，并以B2C网站为研究对象，揭示了其市场中存在的幂律分布规律。

传统市场经济、金融领域基于幂定律的研究有很多，但在电子商务领域幂律分布的研究还十分缺乏。因此，本文将基于幂律分布研究电子商务市场的竞争结构以及其动态变化规律，从定量和动态的角度形成对电子商务整个发展历程的清晰认识和对未来发展的预测，为这一研究领域的发展提供新的视角，并为企业的发展战略提供指导性建议。本文的研究目标包括以下两个方面：（1）验证电子商务市场的竞争结构符合幂律分布规律。以中国B2C电子商务市场的市场份额和美国B2C电子商务市场的市场份额为研究对象，基于幂定律拟合它们历年的市场竞争结构分布规律。（2）从纵向时间角度，分析得出电子商务市场竞争结构的纵向演化规律。本文首先是从静态角度，基于幂定律拟合它们历年的市场竞争结构分布规律，进而从动态角度，研究幂定律参数的变化规律以得到市场竞争结构动态发展规律。

三、数据收集和理论模型

（一）数据收集

本文的研究对象为中国 B2C 电子商务市场和美国 B2C 电子商务市场。收集到的数据一共分为两个部分：中国 B2C 电子商务 2007年-2013 年市场份额数据和美国 B2C 电子商务 2004年-2013年市场份额数据。

根据中国互联网发展报告所述，2007年国家统计局首次对中国19 267个大中型企业电子商务交易情况进行了调查（中国互联网、中国互联网络信息中心，2008）。因此，本文收集到的中国B2C电子商务市场的数据是从2007年至2013 年。其来源为电子商务年鉴、艾瑞咨询、中国互联网络信息中心、中国电子商务研究中心。针对美国B2C电子商务市场进行数据收集整理，由于美国电子商务的出现早于我国，因此最终收集到的美国B2C电子商务市场的数据是从2004年至 2013年。其来源网址是：http://marketingland.com/、http://www.top500guide.com/、http://investor.officedepot.com。由于报告和网站提供的数据有限以及电子商务行业的发展变化速度较快，因此最终统计结果中有部分数据存在缺失。本文的研究是基于原始数据，没有经过处理，确保了研究的真实可靠性，能够真实反映出中美两国B2C电子商务市场的内在发展规律。

（二）理论模型

针对收集到的中美两国B2C电子商务市场份额数据，一共17个数据集，本文研究首先建立在一元非线性回归模型—幂函数的基础上，以验证中美两国B2C电子商务企业市场排名和其市场份额之间的关系强度及其显著性。接着建立在一元二阶多项式模型的基础上，拟合中美两国B2C电子商务企业市场竞争结构的动态发展规律。

一元非线性回归模型用于分析一个自变量和因变量之间的非线性关系。一般的非线性回归模型可以表示为

式中X是自变量，β是待估的参数，Y 是因变量，ε是随机误差。一元非线性回归模型有很多种，本文研究所选择的模型是幂函数

由于幂函数回归模型可以通过简单的数学变换转换为线性回归模型，因此我们首先对幂函数回归模型进行变换处理，接着采用最小二乘法进行参数估计。对式(2)左右两边同时取对数：

令Y=lny，A=lnβ1，B=β2，X=lnx，误差为δ，则式(3)化为一元线性函数

然后根据一元线性回归最小二乘法估计参数A和B，最小二乘法准则

式中，yi对于第i 次观测，因变量的观测值；yi代表对于第i次观测，因变量的估计值。估计的回归方程的参数A和B为

式中，xi代表对于第i 次观测，自变量的观测值；yi代表对于第i 次观测，因变量的观测值；代表自变量的样本平均值；y 代表因变量的样本平均值。

四、基于幂定律拟合的B2C电子商务市场竞争结构分布规律分析

（一）中国 B2C 电子商务市场中的幂律分布规律

基于中国B2C市场2007-2013年市场份额数据，首先以企业市场份额排名为横轴，每个企业的市场份额为纵轴，绘制历年的散点图；接着添加趋势线，分别形成每一年市场竞争结构分布规律的拟合曲线。拟合曲线的方程为p(x)=cx−a。经分析可得，中国B2C电子商务市场的竞争结构服从幂律分布规律。分析结果如图1所示。

图1 2007年-2013年中国B2C市场幂律分布规律变化图

利用SPSS软件对基于幂定律拟合的市场竞争结构分布规律进行进一步分析，得到了F检验和t检验的P值。将中国B2C市场2007年到2013年的市场份额数据基于幂定律拟合的分析结果整理见表1。

表1 中国B2C电子商务市场2007-2013年基于幂定律拟合的分析结果

通过表1可以看出，幂定律拟合的可决系数均大于0.74，且F检验和t检验的P值均小于0.05，回归拟合结果令人满意，表明模型在统计意义上十分显著。分析结果表明中国B2C电子商务市场的竞争结构符合幂律分布特征，即商家的市场份额与其对应的排名成反比关系，少数的商家占据了整个市场中大部分的份额。

（二）美国 B2C 电子商务市场中的幂律分布规律

图2 2004-2013年美国电子商务市场幂律分布规律变化图

以同样的方法对美国B2C电子商务市场的竞争结构分布规律进行分析，拟合方程同上。分析可得，美国B2C电子商务市场的竞争结构服从同样幂律分布规律。分析结果如图2所示。

对基于幂定律拟合的美国B2C电子商务市场的竞争结构的结果进行显著性检验和拟合优度判定，分析结果见表2。

表2 美国B2C电子商务市场2004-2013年基于幂定律拟合的分析结果

通过表2可以看出，幂定律拟合的可决系数均大于0.81，且F检验和t检验的P值均小于0.05，回归拟合结果令人满意，表明拟合模型在统计意义上十分显著。分析结果表明，美国B2C电子商务市场的竞争结构符合幂律分布特征，即商家的市场份额与其对应的排名成反比关系，整个市场中大部分的份额集中在少数商家中。

五、基于幂定律参数变化规律的B2C电子商务市场竞争结构动态发展规律分析

（一）基于幂定律参数变化规律的中国B2C电子商务市场竞争结构动态发展规律分析

在上一章中，已验证历年中美两国B2C电子商务市场竞争结构符合幂律分布规律，即少数几个商家拥有大部分的市场份额。在此基础上，本章将继续探索服从幂律分布特征的市场竞争结构的动态变化趋势—是更加趋于垄断，还是竞争变得更加充分—最终得到中美两国B2C电子商务市场竞争结构随时间变化的动态发展规律。

在SPSS中，用表1中的幂指数α和系数C以及年份建立工作表，利用回归分析中的曲线估计工具，以时间为自变量，并分别以幂律曲线的历年系数变化和历年指数变化为因变量，进行曲线拟合。通过比较不同模型的拟合效果，可知指数模型的拟合效果最优，分析结果见表3、表4与图3、图4。

1.中国B2C市场幂方程系数变化曲线拟合

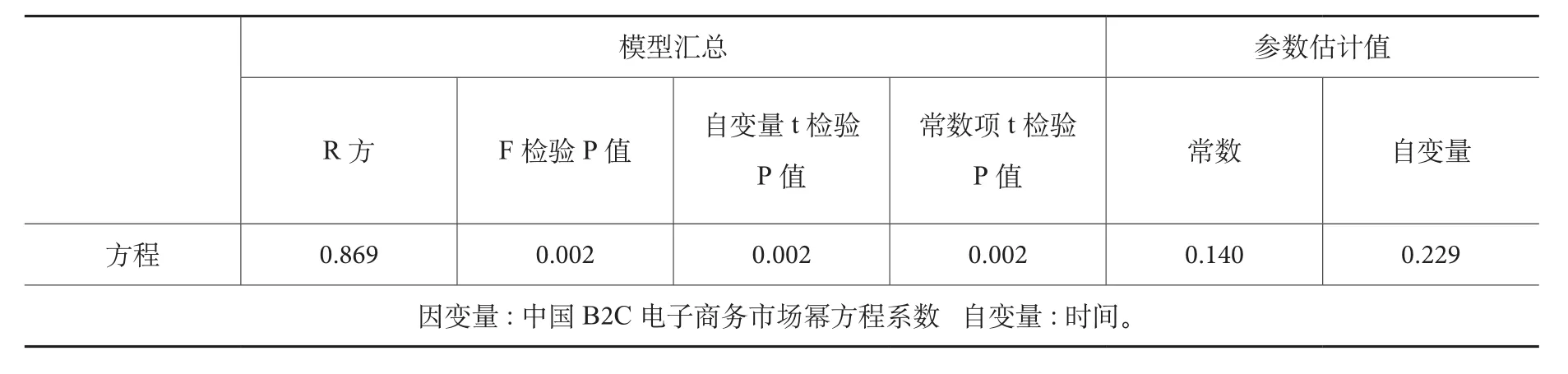
表3 中国B2C市场2007-2013年幂方程系数变化模型汇总和参数估计值

图3 中国B2C市场2007-2013年幂方程系数变化曲线拟合

拟合中国B2C市场2007年到2013年幂方程系数变化的指数回归方程为：

由表3的分析结果可知，模型的可决系数为86.9%，表明指数模型对中国B2C市场2007年到2013年幂方程系数变化的拟合程度很好，F检验和t检验的P值均小于0.01，在统计意义上非常显著，即幂方程的系数随时间变化整体呈现递增趋势。

2.中国B2C市场幂方程指数变化曲线拟合

表4 中国B2C市场2007-2013年幂方程指数变化模型汇总和参数估计值

图4 中国B2C市场2007-2013年幂方程指数变化曲线拟合

拟合中国B2C市场2007年到2013年幂方程指数变化的指数回归方程为：

由表4的分析结果可知，模型的可决系数为89.5%，表明指数模型对中国B2C市场2007年到2013年幂方程指数变化的拟合程度很好，F检验和t检验的P值均小于0.01，在统计意义上非常显著，即幂方程的指数随时间变化整体呈现递增趋势。

（二）基于幂定律参数变化规律的美国B2C电子商务市场竞争结构动态发展规律分析

基于幂定律的参数变化，进而研究美国B2C电子商务市场竞争结构动态发展规律。分析方法同上，在SPSS中，用表2中的幂指数α和系数C以及年份建立工作表，通过回归分析曲线估计工具比较不同模型的拟合效果，可知二次曲线的拟合效果为最优，这与在中国B2C市场得到的模型不同，分析结果见表5、表6与图5、图6。

1.美国B2C市场幂方程系数变化曲线拟合

表5 美国B2C市场2004-2013年幂方程系数变化模型汇总和参数估计值

图5 美国B2C市场2004-2013年幂方程系数变化曲线拟合

拟合美国B2C市场2004年到2013年幂方程系数变化的二次曲线回归方程为：

由表5的分析结果可知，模型的可决系数为97.3%，表明指数模型对美国B2C市场2004年到2013年幂方程系数变化的拟合程度很好，F检验的P值为0.000非常显著， t检验的P值均小于0.05非常显著，即幂方程的系数随时间变化整体呈现递增趋势。

2.美国B2C市场幂方程指数变化曲线拟合

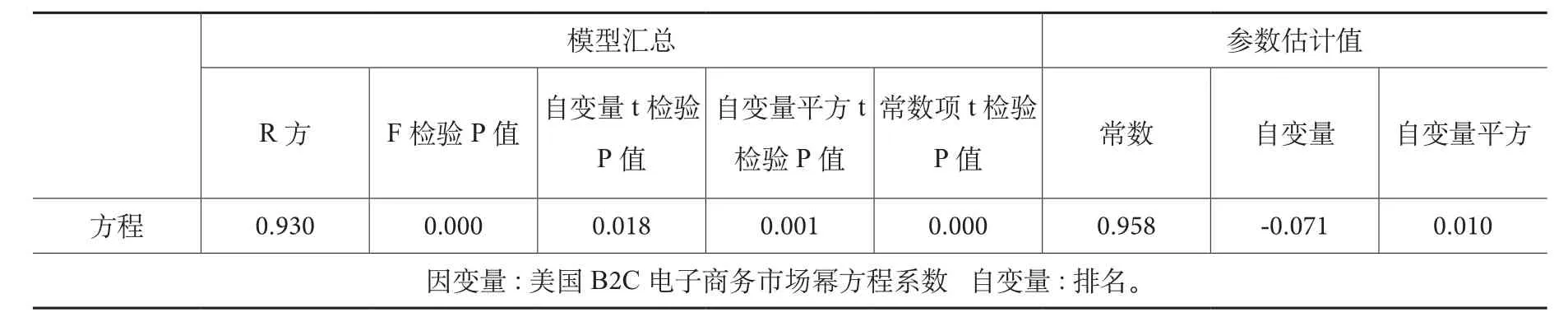
表6 美国B2C市场2004-2013年幂方程指数变化模型汇总和参数估计值

图6 美国B2C市场2004-2013年幂方程指数变化曲线拟合

拟合美国B2C市场2004年到2013年幂方程指数变化的二次曲线回归方程为：

由表6的分析结果可知，模型的可决系数为93%，表明指数模型对美国B2C市场2004年到2013年幂方程系数变化的拟合程度很好，F检验的P值为0.000非常显著，t检验的P值均小于0.05非常显著，即幂方程的系数随时间变化整体呈现递增趋势。

六、结论和意义

（一）中美两国B2C电子商务市场竞争结构幂定律拟合结果

本文基于中国2007年-2013年和美国2004年-2013年B2C电子商务的市场份额数据，通过运用SPSS软件中回归拟合分析工具验证了存在于中美两国B2C电子商务市场竞争结构中的幂律分布规律。研究结果表明，中国B2C电子商务竞争结构幂律拟合结果的可决系数在74% -97%之间变化。经F检验与t检验，P值均小于0.05，表明模型在统计意义上显著，即中国B2C电子商务市场的竞争结构符合幂律分布特征。美国B2C电子商务竞争结构幂律拟合结果的可决系数在81% -98%之间变化。经F检验与t检验， P值均小于0.05，表明模型在统计意义上显著，即美国B2C电子商务市场的竞争结构符合幂律分布特征。本文得出结论，中美两国B2C电子商务市场竞争结构均服从幂定律，电子商务企业的市场份额和它们的市场排名之间存在着幂律关系，即B2C电子商务市场中大部分的市场份额集中在少数商家中。

（二）中美两国B2C电子商务市场竞争结构动态变化规律

对于中国B2C电子商务市场，拟合的历年市场竞争结构的幂曲线的指数和系数整体都呈现出上升趋势，且基于指数回归模型对指数和系数变化规律的拟合效果最好。F检验表明变量之间存在显著关系，即中国B2C电子商务市场竞争结构的幂律曲线的指数和系数与时间存在着显著的相关关系。随着时间的变化，拟合曲线的指数和系数逐渐递增，表明电子商务市场的竞争结构趋于垄断，即强者越强。

相对于中国B2C电子商务市场，美国B2C电子商务市场中拟合的历年市场竞争结构的幂曲线的指数和系数虽然整体也都呈现出上升趋势，但在初始的四年中呈现出下降的趋势，之后逐渐增长。对于美国B2C电子商务市场，与中国B2C电子商务市场不同，它基于二次回归模型对指数和系数变化规律的拟合效果是最好的。F检验表明美国B2C电子商务市场竞争结构的幂律曲线的指数和系数与时间也存在着显著的相关关系。随着时间的变化，拟合曲线的指数和系数首先呈现出下降的趋势接着逐渐递增，表明电子商务市场的竞争结构在经过一段时间的波动之后逐渐趋于垄断，即强者越强。

（三）意义

本文的研究结果给电子商务企业在未来发展过程中做决策时提供了重要的理论依据。中国电子商务正处于一个迅速发展和变革的时期，面对如此激烈的市场竞争环境，无论是在市场中已占据一定份额的企业还是意欲进入市场的企业，他们都需要清楚地了解到存在于现有市场的客观发展规律。本文从理论角度揭示了B2C电子商务市场竞争结构的幂律分布规律，即在B2C电子商务市场竞争中企业占有的市场份额和它的排名之间存在着y=cx-a的函数关系。因此，如果一个企业计划提高自己的市场排名，他可以根据该市场排名相对应的市场份额制定合理的资金投入计划，以确保资金的充分利用，避免资金不足和浪费；对于准备进入这个市场的新企业，通过清楚地了解现有市场的竞争结构并根据其自身的资源状况，合理地估计出其进入市场后可以拥有的市场份额，从而确保企业的投资计划低风险高回报。由此可见，本文的研究成果对B2C电子商务市场的企业具有相当重要的现实指导意义。

[1] 《1997-2009：中国电子商务十二年调查报告》.中国电子商务研究中心.2009.9

[2] 《2013年度中国电子商务市场数据监测报告》.中国电子商务研究中心.2014.3

[3] 高建敏, 王炳兴.中国财富分布规律的实证研究[J].浙江工商大学学报, 2007 (01): 61-65.

[4] 高瑞泽.电子商务生态群落内部演化和竞争机理研究[D].北京交通大学, 2012.

[5] 胡海波, 王林.幂律分布研究简史[J].物理, 2005(12): 889-96.

[6] 吉翔, 高英.中国股市的泡沫与反泡沫——基于对数周期性幂律模型的实证研究[J].山西财经大学学报, 2012 (12): 27-38.

[7] 刘臣, 单伟, 于晶.中国学科知识网络的演化研究——基于1981-2010年引文数据[J].系统工程理论与实践, 2013 (02): 430-436.

[8] 施华萍, 柯见洪, 孙策, 林振权.中国人口分布规律及演化机理研究[J].物理学报, 2009(1)：第58卷第1期: 1-8.

[9] 司马则茜, 蔡晨, 李建平.度量银行操作风险的POT幂律模型及其应用[J].中国管理科学, 2009(01): 36-41.

[10] 山石, 邱红.长尾分布、幂律的产生机制和西蒙模型[J].第六届中国管理科学与工程论坛论文集.上海: 第六届中国管理科学与工程论坛, 2008: 886-890.

[11] 王渊, 杨姝, 王刊良.电子商务研究方向的分类研究:中国视角[J].情报杂志, 2008(11): 87-90.

[12] 杨波, 陈忠, 段文奇.复杂网络幂律函数标度指数的估计与检验[J].上海交通大学学报, 2007(07): 1066-1073.

[13] 俞宣伊.我国C2C电子商务交易网络及其演化机制[D].哈尔滨工业大学, 2010.

[14] 叶作亮, 王雪乔, 宝智红, 陈滨桐.C2C环境中顾客重复购买行为的实证与建模[J].管理科学学报, 2011(12): 71-78.

[15] 张宇, 张建玮, 王正行.金融市场中幂律分布的经验和理论研究进展——经济物理学研究的一个前沿[J].物理, 2004(10):734-740.

[16] 中国互联网、中国互联网络信息中心, 《中国互联网发展报告》.2008.

[17] Ngai E W T, Wat F K T.A Literature Review and Classification of Electronic Commerce Research[J].Information & Management,2002 (39): 416-428.

[18] Jie Li, Baoying Jiao, Yunfeng Wang, Zhipeng Li, A review of electronic commerce research in China[C].The international conference on E-business and e-govrenment, May 7-9, 2010, Guangzhou, China.

[19] LP Kadanoff.From simulation model to public policy An examination of Forrester's[J].Urban Dynamics Simulation, 1971, 16.6: 261-268.

[20] EW Montroll, WW Badger.Introduction to quantitative aspects of social phenomena[J].1974.

[21] Adrian Dr gulescu, Victor M.Yakovenko.Exponential and power-law probability distributions of wealth and income in the United Kingdom and the United States[J].Physica A, 2001, 299(1-2): 213-221.

[22] Anders Johansen, Didier Sornette.Log-periodic power law bubbles in Latin-American and Asian markets and correlated anti-bubbles in Western stock markets: An empirical study[J].International Journal of Theoretical and Applied Finance, 2001, 4 (6): 853-920.

[23] Aaron Clauset, Cosma Rohilla Shalizi, and M.E.J.Newman.Power-Law Distributions in Empirical Data[J].Siam Review, 2009,51(4): 661-703.