动态特征和静态特征自适应融合的目标跟踪算法

张立朝,毕笃彦,查宇飞,汪云飞,马时平

(空军工程大学航空航天工程学院,陕西西安 710038)

动态特征和静态特征自适应融合的目标跟踪算法

张立朝,毕笃彦,查宇飞,汪云飞,马时平

(空军工程大学航空航天工程学院,陕西西安 710038)

由于大多数目标跟踪算法只采用单一静态特征或单一动态特征对目标建模,但静态特征模型不能描述目标的动态特性,并且很难适应场景复杂、快速移动和旋转等问题;而传统运动光流能够描述局部动态特性,却存在孔径问题.提出一种自适应融合动态特征和静态特征的跟踪方法:通过双向光流预测和误差度量自适应提取动态特征,并提取候选目标区域的静态特征,然后构造融合权重函数有效地融合动态特征和静态特征并以此构造协方差矩阵估计误差椭圆,准确描述目标尺度和方向,实现对目标精确表示;通过on-line参数更新机制对权重分配参数进行更新,实现动态特征和静态特征分配的自适应调节,能够适应目标运动速度的变化和场景变化.实验结果表明,在背景复杂的情况下,当目标快速移动或旋转时,与其他相关算法相比,该算法能够获得更好的跟踪效果.

动态特征;运动度量;静态特征;特征融合;自适应

目标跟踪[1]是计算机视觉的一个重要且基础性的问题,受到大量学者的关注[2-3].目前跟踪主要存在以下几个方面的困难:背景干扰、快速移动、尺度和方向改变、光照变化、遮挡.特征提取时,可以把特征分为动态特征和静态特征.静态特征包括SIFT[4]、BRIEF[5]、Histogram[6]等;而动态特征主要指光流[7].目前基于核跟踪[8]和基于粒子滤波[9]的算法大都是提取静态特征对目标进行建模.文献[10]提出尺度和方向自适应的Mean Shift算法,通过引入矩特征[11],计算误差椭圆（Error Ellipse),较好地估计目标尺度和方向;文献[12]提出EM-shift算法,通过提取颜色直方图,同时估计局部模态的位置和用来近似局部模态尺度的协方差,用协方差估计出椭圆目标框,可以较好地估计目标的尺度.但这些算法都采用单一的静态特征:通过颜色统计直方图构造特征模型,采用颜色特征作为静态特征.为了解决单一静态特征对目标描述不充分的问题,一些学者引入其他静态特征进行跟踪[13-16].文献[13]提出一种自适应分块并融合颜色直方图及SIFT特征的目标跟踪方法;文献[14]提出一种将纹理与颜色特征相结合的鲁棒跟踪算法;文献[15]提出将颜色、边缘和纹理特征进行自适应融合的核跟踪算法.另外,也有学者提出在粒子滤波框架内进行多特征融合,比如文献[16]提出一种融合Color、HoG、LBP、Haar等特征并加权降维的跟踪.

以上算法虽然引入纹理、位置、梯度、边缘、Haar等多个特征,但所构造的多特征模型只是在不同静态特征之间进行融合的,缺少对目标动态特性的描述,难以适应目标与背景颜色相似、目标快速移动的跟踪.为了更准确地描述目标,采用光流预测提取目标的动态特征[17],将静态特征和动态特征相融合:将双向光流预测自适应融入核跟踪框架,提取动态特征,然后将其与静态特征融合.通过融合机制,动态特征与静态特征自适应分配比例.动态特征能够弥补静态特征缺乏动态信息的不足,在不知道关于场景任何信息的情况下跟踪到运动对象,解决了目标背景相似和快速移动的问题;但对于光流预测通常存在孔径问题及其局部特征点易受噪声影响的问题,可通过静态全局匹配进行消除,实现更为鲁棒的跟踪.

1 动态特征提取

采用带反馈的光流预测提取目标动态特征.当相机与场景目标相对运动时,观察到的亮度模式运动称为光流（Optical Flow).光流法满足一定的约束条件,称为光流约束方程

其中,I为灰度值,∇I为灰度值的梯度,It为灰度值对时刻t的偏导.

如图1所示,动态特征预测原理:首先在t时刻图像中提取K个特征点,如图中的三角形;然后从t时刻图像的特征点A跟踪到t+1时刻图像预测点B;最后从t+1时刻B点后向跟踪到t时刻反馈点C,如此生成前向和后向两个轨迹.设特征点A、预测点B、反馈点C的位置坐标集合分别为:ΩK={si}i=1,…,K,Ω′K={s′i}i=1,…,K,Ω″K={s″i}i=1,…,K.两次的预测的计算为

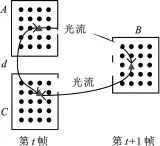
图1 双向光流预测示意图

其中,f（·)为光流函数;Ft表示第t帧图像;Ft+1表示第t+1帧图像.

根据上述分析可知,利用双向光流预测提取动态特征时,可以通过度量前向轨迹与后向轨迹之间的匹配程度进行误差估计.匹配程度为t时刻A和C的距离d,距离d越小,匹配程度越高.为此提出一种度量双向光流预测程度的动态权重函数.如果特征点光流矢量很小,则会造成光流没有预测值,导致基于光流跟踪很容易失败.为此去除无光流预测的特征点,剩余k个特征点,用集合Ωk={si}i=1,…,k表示.反馈误差为

TLD[18]采用中值流算法[19],认为权重函数是关于di的0-1分布函数.而对于实际的di分布,如图2（b)所示,其值越小,说明预测误差越小,匹配程度越高,特征点的贡献程度越大;反之亦然.因此高斯分布函数更能反映权重随反馈误差di反比例变化的趋势,文中采用高斯分布函数描述权重,表达式为

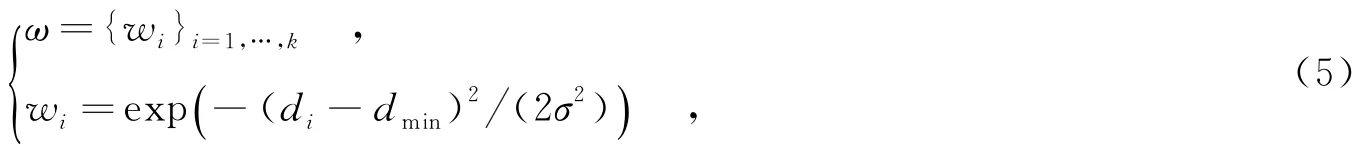
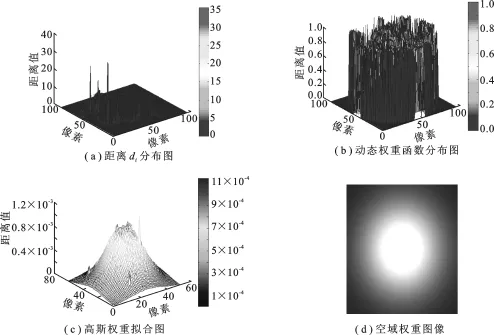
图2 空域动态权重分布图

其中,dmin=min（di),作为动态权重的高斯均值;σ为方差值.其分布如图2（a)所示.

由上文得到的动态权重w′i和位移Δsi,提出一种基于双向光流运动度量的核跟踪算法.通过双向光流提取出目标的运动特征,获得特征点的运动位移Δsi和相应的动态权重w′i,在此基础上利用核算法迭代,搜索出位移密度最大的点.流程如下:

（2)确定动态特征的概率密度函数,即

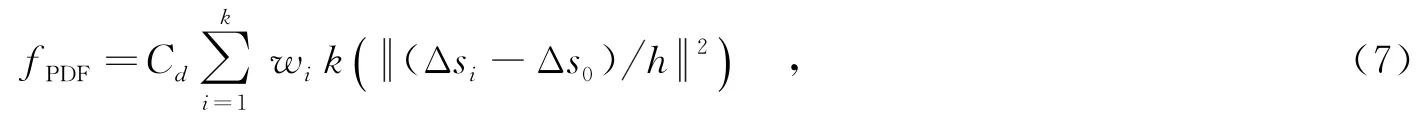
其中,Cd为概率密度函数的系数,k为特征点个数,wi为动态权重.

（3)采用梯度下降法寻找概率密度函数的模值,根据动态权重和核函数的影子核,对特征点位移Δsi进行加权核估计,即

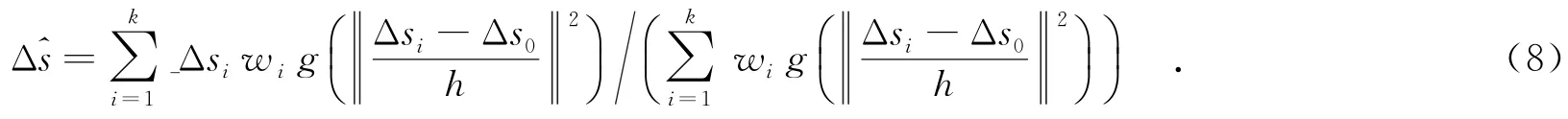
文中利用双向光流提取动态特征时采用金字塔Lucas-Kanade光流法.通过由粗到精的策略将图像在不同分辨率上分层,将在粗尺度下得到的结果作为下一尺度的初始值,在不同分辨率上对图像序列进行光流矢量u计算,能够较好地解决目标快速移动的问题.并且光流矢量u对于与目标相似的背景具有较强的抗干扰性.

2 静态特征的提取

在核跟踪框架内提取目标静态特征,笔者采用颜色直方图统计作为全局静态特征.目标模型和候选目标模型在特征空间中用颜色直方图表示,为了降低边缘像素点权重,采用单调递减凸函数k（x)作为核函数.

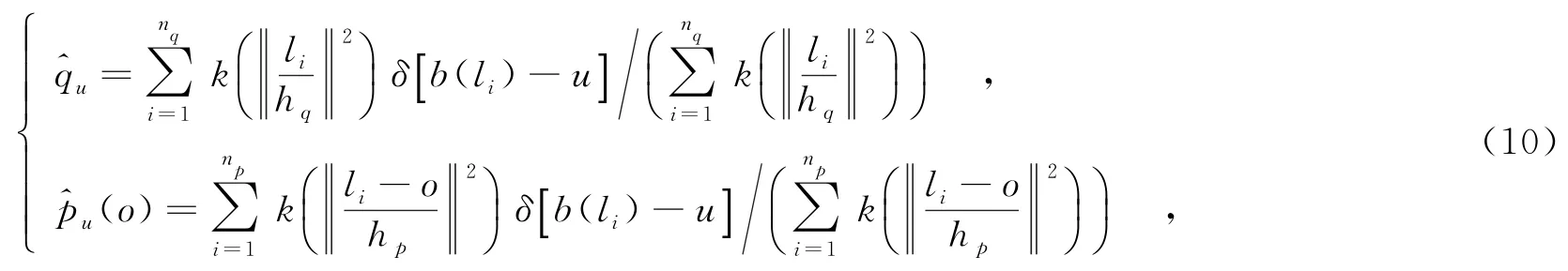
其中,hq和hp表示两个核函数尺度;li为像素坐标;b为像素li直方图区间指示;m指直方图区间数目.目标模型和候选目标模型之间用Bhattacharrya系数相似度量,即

其中,C1和C2为常数;i=1,…n;w′i为静态特征权重,即

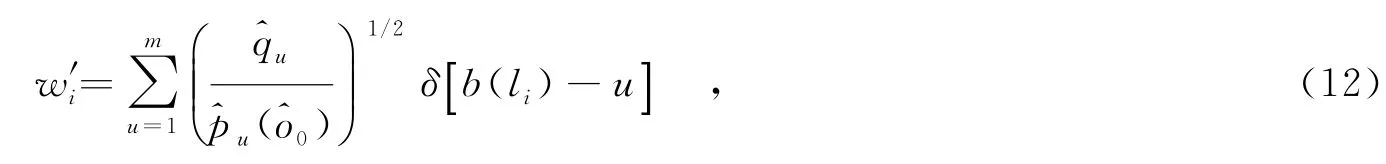
其中,g（x)=-k′（x).

3 目标跟踪算法

首先,通过双向光流预测和误差度量自适应提取动态特征,并提取候选目标区域的静态特征,然后构造融合权重函数,有效地融合动态特征和静态特征并以此构造协方差矩阵估计误差椭圆,准确描述目标尺度和方向,实现对目标精确表示;通过on-line参数更新机制对权重分配参数进行更新.

3.1 初始化

采用椭圆框表示目标:一方面,椭圆形状的目标框对目标的尺度和方向具有良好的适应性;另一方面,颜色直方图对于圆形搜索区域具有很好的旋转不变性.而采用颜色特征作为静态特征,其原因在于颜色直方图具有良好的全局统计特性和对椭圆框的旋转不变特性.采用Maximization-Maximization（MM)scheme[22]进行动态估计和静态估计,直到两个更新迭代都达到收敛.通过权重函数和线性加权融合动态特征和静态特征.融合权重参数设为θ,参数的更新机制在第3.3节中会详细介绍.

局部特征采用Harris角点,全局特征采用直方图.由图3可以看出,目标的动态信息主要分布在目标的边缘轮廓上,通过检测提取目标的角点,然后进行目标运动特征的估计,运动权重服从于高斯分布;目标的静态信息通过候选目标区域的直方图信息统计获得,静态权重服从于直方图分布,目标图像的动态特征和静态特征的权重图像以及两者的融合权重图像如图3所示.图3从左到右分别为:局部动态特征点、区域静态特征点;动态特征、静态特征的提取;动态权重图像、静态权重图像及通过融合得到的融合权重图像

在估计目标尺度时,通过候选目标区域像素位置的加权二阶中心矩计算协方差,进而计算误差椭圆.候选目标区域的像素包括双向光流预测的预测点和其余非预测点.分析式（5),计算动态权重wi时,采用光流前向预测与后向预测之间的匹配度量,包含运动目标的速度度量和空间位置信息,并且由图3可以看出权重主要分布在目标轮廓上,所以能够提取目标丰富的结构信息;分析式（12),计算静态权重w′i时,首先分别统计目标区域和候选目标区域像素的颜色值,然后采用直方图区间对应统计值1/2次方之比,可见静态权重反映像素的全局颜色值和统计值信息.由此可知,动态权重包含目标运动、位置、结构等信息,静态权重包含目标颜色统计信息,因此,对动态权重和静态权重乘性加权融合并计算目标协方差可以更准确地估计目标尺度,进而再将协方差奇异值分解估计目标尺度和方向.融合权重计算为

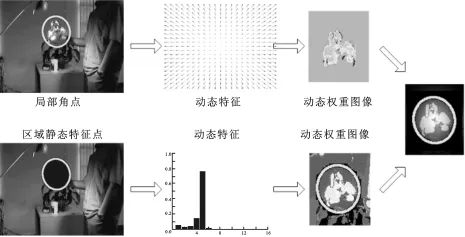
图3 动态权重和静态权重融合示意图

其中,Ω′k为k个预测点集合,Ωnp-k为候选目标区域Ωnp中去除预测点Ω′k的像素集合.动态特征和静态特征通过乘性加权紧密耦合,为计算协方差提供更好的特征描述.

通过MM scheme估计得到最优的动态特征位置与最优的静态特征位置,将最优位置O1与O2加权叠加,得到目标中心位置为

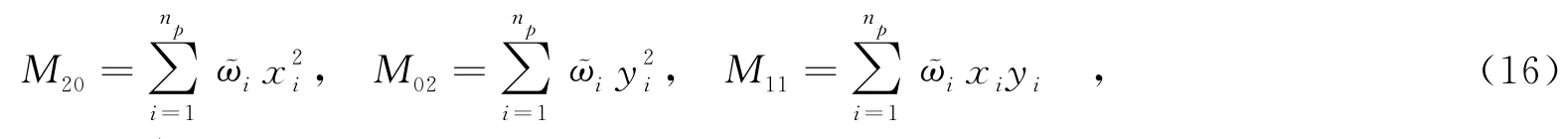
其中,（xi,yi)为Ωnp中li的坐标.

对协方差矩阵Cov奇异值分解为

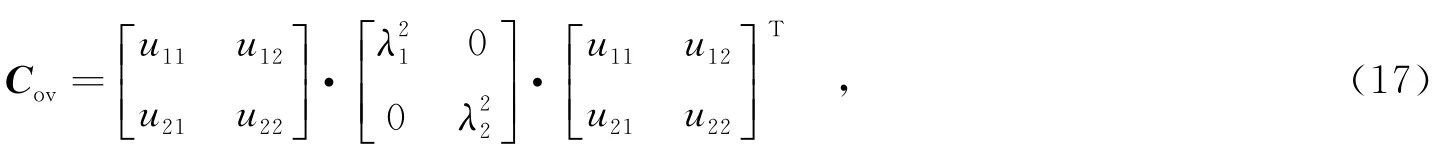
其中,λ1和λ2表示目标的尺度,向量（u11,u21)T和（u12,u22)T分别表示真实目标的两个主轴的方向.

则椭圆目标区域表示为

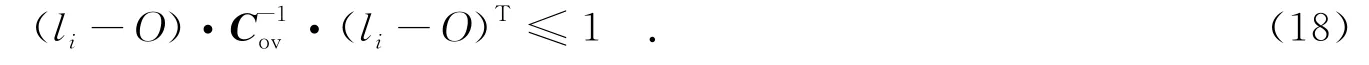
3.2 跟踪过程

算法流程如图4所示.

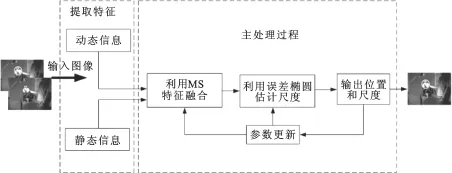
图4 算法流程框图

输入:第t帧图像It,目标模型={u}u=1…m,参数θn-1,初始位置O0,初始椭圆目标框bEb0.输出:（O,bEb0)t,参数θn.

（1)计算Mean Shift迭代:

（a)利用式（9)计算O1,利用式（5)计算动态权重w′i;

（b)利用式（13)计算O2,利用式（12)计算静态权重wi;

（2)利用式（15)计算位置O.

（4)利用式（21)更新参数θn.

3.3 On-line参数更新过程

根据图像内容的变化调整参数的变化,进而对权重分配参数θ进行实时更新.权重分配参数θ根据动态特征重要性程度来评价:核函数对可靠像素的光流矢量进行加权估计,进而估计动态权重在融合权重中所占比例.当较大时,目标像素光流矢量较大;较小时,像素可靠,则参数θML的估计值也相应变大,通过最大化似然估计方法[22]迭代计算:

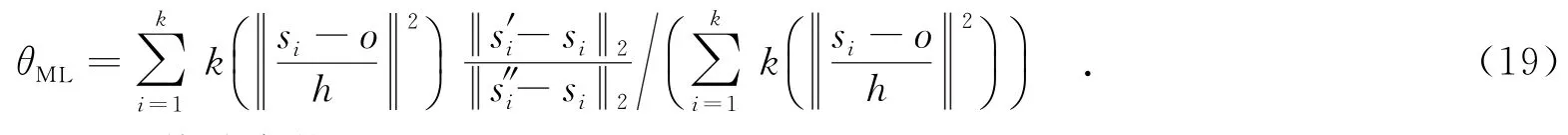
接着,引入先验的θPrior进行估计参数的校正:

一般设想目标运动服从于连续分布,则融合参数也遵循连续变化的趋势.为防止参数估计发生突变引入前一时刻参数值进行校正,得到最终的参数更新值

4 实验结果及其分析

所有实验在Intel（R)Xeon（R)CPU W3550 3.07 GHz 3.06 GHz,6 GB内存的64位计算机上进行.算法通过MATLAB 2013a实现.测试视频来自于多实例学习跟踪[20]中含有与目标背景相似、快速移动、尺度和旋转变化的4段视频.实验中,Lucas-Kanade光流金字塔层数为2层,特征点选择500个,特征模型均采用Epanechnikov核[8]作为空间加权的核函数,各视频中动态权重函数w′i的方差σ=0.05,权重分配参数初始化θPrior=0.5,先验参数值固定为ωPrior=0.25,ML评估器通过式（19)进行计算,MA参数固定为γMA=0.4.所有参数在整个实验中都设为固定值,采用第1帧中提取的目标模型作为模板.实验比较算法: SOAMST[10]、EM-shift[12]、Mean Shift算法[8]和TLD算法[18],代码均来自作者的公开代码.

4.1 定性分析

如图5所示,第1列是“Sylvester”部分结果（其中,SOAMST为实线,TLD为虚线,EM-shift为点线,MS为点划线,文中算法为加粗实线).视频中,背景比较相似,目标玩具姿态和方向不停变化.选取几帧代表性的视频帧:目标扬起、低下、旋转、尺度、光照变化.SOAMST、EM-shift和MS采用单一的颜色特征描述目标,容易被目标身后的花盆背景及人的手臂所干扰,如在第270、850帧,并且都不能适应目标的尺度和旋转变化;TLD算法采用单一的运动特征,在跟踪光照变化剧烈的第729帧时,开始跟丢;文中算法通过融合动态特征和静态特征,发挥各自优势,弥补特征缺陷,可以很好跟踪.第2列是“David2”结果.对其头部跟踪,主要有姿态旋转等变化并且刚开始黑色板背景对均值漂移的干扰比较大.由结果可以看出,采用颜色直方图的均值漂移算法SOAMST、MS和EM-shift在一开始便漂移到整个黑色板上,这是由于黑色板上的像素灰度值非常密集,根据均值漂移原理,找灰度概率密度最大的点,因此在刚开始便找到黑板的中心,丢失目标,如第260帧;而文中算法通过融合动态特征可以很精确跟踪目标,对目标较大变化,如低头（第363帧)、旋转（第463帧)都能很好适应;TLD的矩形跟踪框不能适应目标这些变化.

4.2 定量分析

采用3个标准[21]比较文中算法与其他算法:中心误差（Localization Error),覆盖率（overlap),精确度.

图5 部分视频跟踪结果

由定量分析结果可以看出,文中算法的平均错误率和方差在两个视频中都是最好的,在其余两个视频中接近最好;在成功率评价方面,文中算法在4个视频中都是最好的,其中在视频“Football”跟踪中,甚至达到100%的成功率.文中算法的精度曲线斜率在3个视频中都是最快的,另一个视频也接近最快.

SOAMST和EM-shift算法对于背景的相似度有很强的敏感性,当跟踪序列出现与目标相似的背景时,很容易跟踪失败,甚至在视频刚开始便丢失目标,导致成功率为0,如序列“David2”,而且两者对搜索区域内所有的点进行计算,跟踪效率很低;TLD算法依赖局部结构特征,当目标发生尺度变化时,匹配误差增大,容易丢失目标,但由于加入检测算法对跟踪算法进行初始化,消除跟踪失败带来的影响,所以对一些视频跟踪结果较好;MS不能适应目标尺度和旋转的变化,并且跟踪效率非常低;文中算法将动态特征与静态特征相融合,结合矩特征估计误差椭圆,在4个目标与背景相似、快速移动、尺度和旋转变化的视频中,与最新和相关跟踪算法相比,具有很高的准确度和精确度,实现鲁棒跟踪.定量实验结果如图6和表1所示.

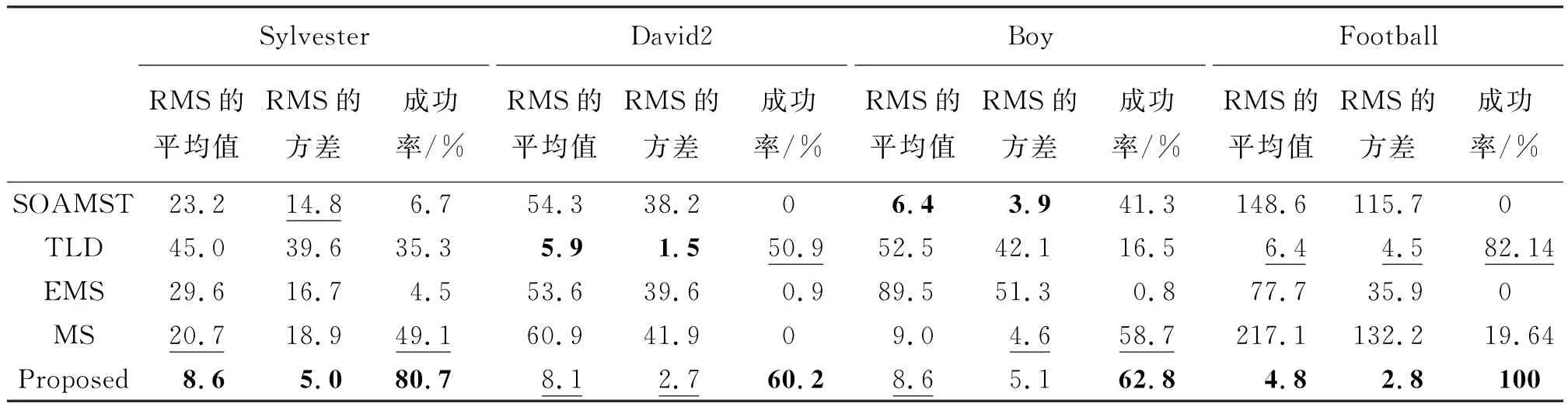
表1 RMS的平均值、方差、成功率和权重比例

5 结束语

通过误差度量自适应提取动态特征,并提取目标区域静态特征,构造权重融合函数有效地融合动态特征和静态特征,利用融合权重构造协方差矩阵估计误差椭圆,准确描述目标尺度和方向,实现对目标的精确表示;通过on-line参数更新机制对权重分配参数进行在线更新,实现动态特征和静态特征分配的自适应调节,能够适应目标运动速度的变化和场景变化,解决背景复杂和快速移动的跟踪问题.

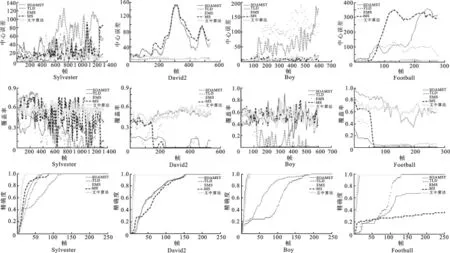
图6 中心误差,覆盖率和精确度实验结果图

[1]侯志强,韩崇昭.视觉跟踪技术综述[J].自动化学报,2006,32(4):603-617. Hou Zhiqiang,Han Chongzhao.A Survey of Visual Tracking[J].Acta Automatica Sinica,2006,32(4):603-617.

[2]Yang H X,Shao L,Zheng F,et al.Recent Advances and Trends in Visual Tracking[J].Eurocomputing,2011,74(8): 3823-3831.

[3]Smeulders A,Chu D,Cucchiara R,et al.Visual Tracking:an Experimental Survey[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,36(7):1442-1468.

[4]Lowe D G.Scale&Affine Invariant Interest Point Detectors[J].International Journal of Computer Vision,2004,60 (1):63–86.

[5]Calonder M,Lepetit V,Fua P,et al.BRIEF:Binary Robust Independent Elementary Features[C]//Lecture Notes in Computer Science.Heidelberg:Springer Verlag,2010:778-792.

[6]Leichter I.Mean Shift Trackers with Cross-Bin Metrics[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34(4):695-706.

[7]Bouguet J Y.Pyramidal Implementation of the Lucas Kanade Feature Tracker Description of the Algorithm[Z].Intel Micro-processor Research Labs,1999.

[8]Comaniciu D,Ramesh V,Meer P.Kernel-based Object Tracking[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2003,25(5):564-577.

[9]Lim J,Ross D A,Lin R S,et al.Incremental Learning for Visual Tracking[C]//Advances in Neural Information Processing Systems.Canada:NIPC.2004:793-800.

[10]Ning J F,Zhang L,Zhang D,et al.Scale and Orientation Adaptive Mean Shift Tracking[J].IET Computer Vision,2012,6(1):52-61.

[11]Mukundan R,Ramakrishnan K R.Moment Functions in Image Analysis:Theory and Applications[M].Singapore: World Scientific Publishing,1998.

[12]Zivkovic Z,Kröse B.An EM-like Algorithm for Color-Histogram-Based Object Tracking[C]//Proceedings of the IEEEComputer Society Conference on Computer Vision and Pattern Recognition.Los Alamitos:IEEE Computer Society,2004:798-803

[13]董文会,常发亮,李天平.融合颜色直方图及SIFT特征的自适应分块目标跟踪方法[J].电子与信息学报,2013,35 (4):770-776.Dong Wenhui,Chang Faliang,Li Tianping.Adaptive Fragments-based Target Tracking Method Fusing Color Histogram and SIFT Features[J].Jounal of Electronics&Information Technology,2013,35(4):770-776.

[14]Bousetouane F,Dib L,Snoussi H.Improved Mean Shift Integrating Texture and Color Features for Robust Real Time Object Tracking[J].The Visual Computer,2013,29(3):155-170.

[15]Yin H P,Chai Y,Yang S X,et al.An Improved Mean-shift Tracking Algorithm Based on Adaptive Multiple Feature Fusion[C]//Lecture Notes in Electrical Engineering.Heidelberg:Springer Verlag,2012:49-62.

[16]Chen W H,Cao L J,Zhang J G,et al.An Adaptive Combination of Multiple Features for Robust Tracking in Real Scene [C]//Proceedings of the IEEE International Conference on Computer Vision.Piscataway:IEEE,2013:129-136.

[17]Chen E,Xu Y,Yang X,et al.Quaternion Based Optical Flow Estimation for Robust Object Tracking[J].Digital Signal Processing,2013,23(1):118-125.

[18]Kalal Z,Mikolajczyk K,Matas J.Tracking Learning Detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,6(1):1-14.

[19]Kalal Z,Mikolajczyk K,Matas J.Forward-backward Error:Automatic Detection of Tracking Failures[C]//Proceedings of International Conference on Pattern Recognition.Piscataway:IEEE,2010:2756-2759.

[20]Babenko B,Belongie S,Yang M H.Visual Tracking with Online Multiple Instance Learning[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops.Piscataway:IEEE Computer Society,2009:983-990.

[21]Everingham M,Van Gool L,Williams C K,et al.The pascal Visual Object Classes(VOC)Challenge[J].Interational Journal of Computer Vision,2010,88(2):303-338

[22]Oron S,Bar-Hillel A,Levi D,et al.Locally Orderless Tracking[J].International Journal of Computer Vision,2012,111(2):213-228.

（编辑:王 瑞)

Research on visual object tracking by fusing dynamic and static features

ZHANG Lichao,BI Duyan,ZHA Yufei,WANG Yunfei,MA Shiping
(School of Aeronautics and Astronautics Engineering,Air Force Engineering Univ,Xi’an 710038,China)

Traditionally,most tracking algorithms only use the single static feature or single dynamic feature to model the object.The static feature based model can not describe the object’s dynamic characteristics and is difficult to adapt to the changing object with a background cluster,abrupt movement and rotations.While the classical optical flow is able to describe local dynamic characteristics,it has aperture issues.Therefore,we present a new tracking method based on fusing the dynamic and static features adaptively:the dynamic feature is extracted by the bidirectional optical flow and error metric adaptively,and is fused with the static feature by the fusion weight efficiently.The fusion weight based covariance is constructed to evaluate error ellipse which describes the object’s scale and orientation exactly;the weight assignment parameter is updated by an on-line parameter updating mechanism,which balances the dynamic feature and static feature and ensures the tracking adaptation to the object’s velocity and scene changes.Experiments show that the proposed algorithm can achieve better tracking results compared with the related algorithms,on the occasions when the object moves abruptly and rotates with a background cluster.

dynamic feature;motion metric;static feature;features fusion;adaptation

TP391

A

1001-2400（2015)06-0164-09

10.3969/j.issn.1001-2400.2015.06.028

2014-05-28

时间:2015-03-13

国家自然科学基金资助项目（61472442,61203268,61202339)

张立朝（1990-),男,空军工程大学硕士研究生,E-mail:zlichao2012@163.com.

查宇飞（1980-),男,副教授,E-mail:zhayufei@126.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20150313.1719.028.html