一种新的角度多普勒补偿方法

冯为可,张永顺,张 丹

(1.空军工程大学防空反导学院,陕西西安 710051；2.西安电子科技大学电子工程学院,陕西西安 710071)

一种新的角度多普勒补偿方法

冯为可1,张永顺1,张 丹2

(1.空军工程大学防空反导学院,陕西西安 710051；2.西安电子科技大学电子工程学院,陕西西安 710071)

由于机载非正侧雷达杂波空时耦合关系存在严重的距离依赖性,故训练样本单元与待测单元的杂波不服从独立同分布.角度多普勒补偿方法是补偿杂波距离依赖性的有效手段,但在系统存在速度误差和角度误差时,杂波依赖性补偿性能下降.针对这个问题,提出了基于稀疏恢复的角度多普勒补偿方法——SR-ADC方法.该方法首先对训练样本单元和待测单元的雷达回波数据进行稀疏恢复得到杂波空时谱;然后确定杂波谱中心及其空间频率和多普勒频率,并以此计算空时转换矩阵,使训练单元杂波与待测单元杂波分布特性趋于一致.与常规角度多普勒补偿相比,SR-ADC方法能够实现杂波距离依赖性的自适应补偿,在存在误差时也能取得较为理想的补偿.

机载非正侧阵雷达;杂波距离依赖性;角度多普勒补偿;稀疏恢复

机载雷达具有空中警戒、侦察、控制和制导武器等功能,在我国国防建设中发挥着重要作用.机载雷达在下视时,由于地面杂波分布范围广、强度大,动目标被完全掩盖而无法识别.如何对地面杂波进行有效抑制,是机载雷达信号处理的重要内容.其中,空时自适应处理（Space Time Adaptive Processing,STAP)[1-2]方法是抑制地面杂波、补偿平台运动引起的杂波谱展宽、检测地面慢速目标的有效手段.杂波协方差矩阵（Clutter Covariance Matrix,CCM)是空时自适应处理方法杂波抑制性能的决定性因素,在实际应用中,待测单元的杂波协方差矩阵是利用与待测单元独立同分布（Independent Identically Distributed,IID)的临近训练样本单元,通过采样协方差求逆（Sample Matrix Inversion,SMI)[3]方法估计得到的,以实现自适应的杂波抑制.为了使空时滤波器的输出信杂噪比损失小于3 d B,用来估计杂波协方差矩阵的独立同分布的训练样本数需大于系统自由度的两倍.对于非正侧视阵,地面杂波多普勒频率具有严重的距离依赖性,尤其在近程条件下,距离依赖性更加显著,使得杂波分布不满足独立同分布条件,进而无法以训练样本来准确估计待测单元的杂波协方差矩阵,使空时自适应处理方法的杂波抑制性能下降[4-5].

补偿距离依赖性的方法有很多,包括多普勒弯曲（Doppler Warping,DW)[6]、角度多普勒补偿（Angle Doppler Compensation,ADC)[7]、空时内插补偿（Space Time INTerpolating technique,STINT)[8]和基于配准补偿（Registration Based Compensation,RBC)[9]等方法.其中,角度多普勒补偿方法由于简单且快速,补偿效果较好而被广泛运用.该方法通过在空间角度域和多普勒域的补偿将各训练样本单元和待测单元的杂波特性配准,计算杂波转换矩阵,从而在一定程度上抑制杂波距离依赖性.对于主瓣杂波,该方法的补偿效果更为明显.然而,在实际应用中,角度多普勒补偿方法中每个训练样本的杂波转换矩阵都需要根据载机平台提供的飞行配置参数（例如俯仰角、方位角、偏航角和速度等),利用杂波空时耦合关系计算得到,因而任意配置参数的误差都会对该方法的杂波距离依赖性补偿性能造成一定的影响.

针对上述问题,笔者提出了一种基于稀疏恢复[10-11]的角度多普勒补偿方法（Sparse Recovery-Angle Doppler Compensation,SR-ADC).该方法首先对不同距离单元的回波数据进行稀疏恢复,得到杂波空时分布谱;接着确定杂波空时谱中心对应的空间频率和多普勒频率;然后计算训练样本空时转换矩阵,将训练样本单元回波数据与待测单元的回波数据进行配准;最后根据变换后的训练样本有效地估计待测距离单元的杂波协方差矩阵,进而设计滤波器对杂波进行抑制.理论分析和实验仿真表明,该方法可以实现杂波距离依赖性的自适应补偿,提高主瓣杂波的补偿效果,在存在误差时也能获得较好的处理性能.

1 信号模型及角度多普勒补偿方法

1.1 杂波模型

机载非正侧雷达杂波的空间耦合关系为

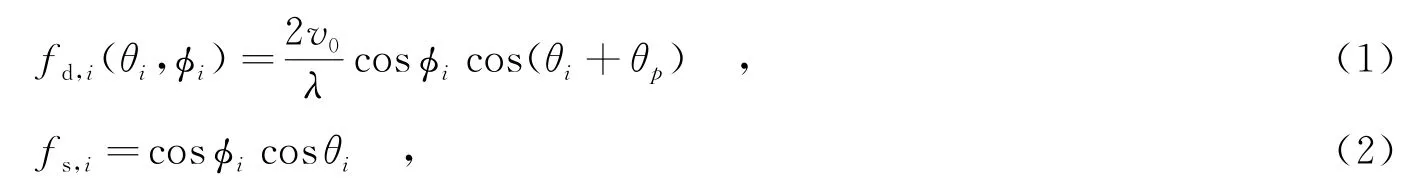
其中,θi和ϕi分别为第i个杂波块对应的方位角和俯仰角;v0为载机速度;θp为天线阵面与载机速度之间的夹角.

对第l个距离单元的杂波进行分块,则该距离单元的杂波可以等效为多个离散杂波块叠加而成:

其中,P为离散杂波块个数;σi为第i个杂波块对应的散射系数;wt和ws分别为杂波对应的归一化多普勒频率和空间频率;Si（wt,ws)为杂波对应的空时二维导向矢量.Si（wt,ws)可表示为

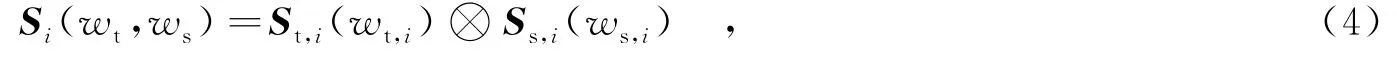
其中,St,i（wt,i)和Ss,i（ws,i)分别为杂波对应的时域导向矢量和空域导向矢量,表示为

其中,wt,i=2πfd,ifprf,ws,i=2πdfs,iλ;N、K分别为天线阵元数和相干脉冲数;fd,i、fs,i分别为杂波对应的多普勒频率和空间频率;fprf为雷达脉冲重复频率;d和λ分别为阵元间距和波长.

1.2 角度多普勒补偿方法

在非正侧阵条件下,角度多普勒补偿算法的基本原理是根据杂波谱的空时耦合关系计算出各距离单元杂波谱中心的位置,将各参考单元的杂波分别沿空间锥角和多普勒方向移动,使得平移后各参考单元的杂波谱中心与待检测单元的杂波谱中心重合.

假设第l个距离单元杂波的俯仰角为ϕl,天线主波束指向的方位角为θ0,则根据式（4)可以计算其杂波谱中心的归一化多普勒频率为

同样可得杂波谱中心的归一化空间频率为

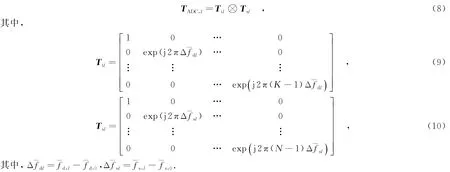
经过角度多普勒补偿后的第l个距离单元的雷达回波数据为

2 基于稀疏的角度多普勒补偿方法——SR-ADC方法

由以上的分析可知,角度多普勒补偿方法的补偿性能取决于事先根据飞行配置信息（主波束方位角θ0、杂波俯仰角ϕl和速度v0等)和杂波空时耦合关系计算得到的杂波谱中心的多普勒频率和空间频率.当飞行配置参数存在误差时,角度多普勒补偿方法的杂波距离依赖性补偿性能将会大幅下降.因此,笔者提出了一种基于稀疏恢复的角度多普勒补偿方法,称为SR-ADC方法,具体分析如下.

首先将空间频率和多普勒频率分别遍历并离散为Ns=ρsN,Nd=ρdK个分辨单元,构造超完备基矩阵Ψ:

其中,ρs和ρd分别表示空间频率和多普勒频率的离散化程度,为保证高分辨,一般选它们远大于1;Sq（wt,q,ws,q)为第q个空时导向矢量,由式（4)计算得出;wt,q和ws,q分别为对应的多普勒频率和空间频率.

机载雷达杂波是由多个不同空间频率和多普勒频率的回波数据叠加而成的,则第l个距离单元的杂波回波数据可以表示为

其中,γq为杂波在第q个空时导向矢量上的复幅度;,代表雷达回波数据在空间频率-多普勒频率域上的幅度分布,即杂波空时谱.

杂波空时谱αl的估计等价于在方程（13)中已知Xl和Ψ而求解αl.由于Ψ的列数NsNd远大于行数NK,因此方程（13)属于欠定方程,存在多个可能解.根据稀疏恢复理论[11],当杂波空时谱αl具有稀疏性时,方程的求解可转化为典型的稀疏恢复问题进行求解:

针对上述问题的求解方法主要有3种,即l1范数最小化方法[12]、FOCUSS（FOCal Underdetermined System Solver)算法[13]和MP（Matching Pursuit)算法[14].其中,基于迭代加权l2最小范数的FOCUSS算法,计算量相比于l1范数最小化方法大大降低,利用后验知识进行迭代加权,避免了误差带来的不利影响.综合考虑算法性能和计算量,笔者选择FOCUSS算法进行计算.

由于杂波空时谱αl表示杂波在不同空间频率和多普勒频率下的幅度分布,可以实现杂波特性的高分辨估计,因此为了避免角度多普勒补偿方法受误差影响较大等问题,笔者利用得到的杂波空时谱分布确定杂波谱中心,并计算空时转换矩阵,以达到补偿杂波距离依赖性的目的.具体步骤如下:

第1步 在不同距离单元回波数据的空时谱中选取幅度最大点作为杂波谱中心.

第2步 确定杂波谱中心的空间频率和多普勒频率并归一化,第l个距离单元杂波谱中心的多普勒频率和空间频率分别为和

第3步 计算训练样本单元与待测单元杂波谱中心的多普勒频率和空间频率的差值,即

接着,根据式（8)计算第l个训练样本单元的空时转换矩阵TSR-ADC,l.

第4步 将训练样本单元回波数据向待测单元进行补偿,即

在对杂波距离依赖性补偿后,利用采样协方差求逆方法估计待测单元杂波协方差矩阵,计算空时自适应滤波器最优权值,即

3 仿真实验

选取斜侧阵（θp=30°)机载相控阵雷达进行仿真实验.实验条件如下:发射接收阵元数均为10;相干脉冲间隔内的脉冲数为16;阵元间隔为0.16 m;载机高度为6 km,载机速度为120 m/s;波长为0.32 m,脉冲重复频率为2 000 Hz,杂噪比为60 dB,雷达最大作用距离为400 km,雷达主波束方位角为90°,待测单元距离为8.4 km,无距离模糊.

误差设置如下:偏航角为5°,俯仰角误差和方位角误差均为1°,速度误差为5 m/s.实验中将与待测单元最邻近的4个距离样本作为保护单元,接着在待测单元两侧对称地选取2NK个距离单元作为训练样本.稀疏恢复中空间频率和多普勒频率离散化程度均为6,即ρs=ρd=6.

实验1 杂波空时谱估计.本部分仿真未经补偿、经角度多普勒补偿方法补偿和SR-ADC方法补偿后的采样协方差求逆方法估计出的杂波功率谱,并与真实杂波功率谱进行对比.不同方法的杂波功率谱均采用最小方差无失真响应（Minimum Variance Distortionless Response,MVDR)谱.

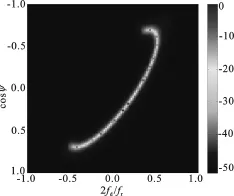
图1 真实杂波功率谱

图2 未经补偿的采样协方差求逆方法的杂波MVDR谱

由图1和图2可以看出,在非正侧阵的情况下,由于杂波具有距离依赖性,使用采样协方差求逆方法直接利用训练样本单元估计待测单元的杂波协方差矩阵,不同距离单元的杂波叠加在一块,会导致杂波谱严重展宽.ψ表示空间锥角.

图3 经角度多普勒补偿方法补偿的杂波MVDR谱估计

图4 经SR-ADC方法补偿的杂波MVDR谱估计

由图3和图4可以看出,由于常规角度多普勒补偿方法是基于俯仰角、方位角和速度等先验信息以及杂波空时耦合关系的,因此当存在误差（偏航角、方位角误差、俯仰角误差和速度误差等)时,常规角度多普勒补偿方法的杂波距离依赖性补偿效果下降,在误差较大时甚至无法对杂波距离依赖性进行补偿;SR-ADC方法利用稀疏恢复方法估计杂波空时谱,不依赖于先验知识,杂波谱中心的多普勒频率和空间频率估计更加准确,补偿效果明显优于常规角度多普勒补偿方法,对于主瓣杂波而言,补偿性能提高更多.

实验2 杂波抑制性能.本部分以改善因子为基准衡量不同方法的杂波抑制性能.其中,改善因子的定义为输出信杂噪比（Signal to Clutter-plus-Noise Ratio,SCNR)与输入信杂噪比的比值.

由图5可以看出,未经补偿利用采样协方差求逆方法估计杂波协方差矩阵进行空时自适应处理时,由于杂波谱展宽,使得杂波抑制性能下降,慢速目标的检测能力严重下降.角度多普勒补偿方法和SR-ADC方法的杂波抑制性能均有提高,但角度多普勒补偿方法受误差影响较大,凹口较宽,而SR-ADC方法可以形成比角度多普勒补偿方法更窄的凹口,慢速目标的检测能力提高5～10 dB.

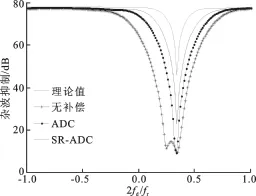
图5 杂波抑制性能比较

4 总 结

笔者提出了基于稀疏恢复的角度多普勒补偿方法.该方法利用稀疏恢复得到杂波空时谱分布,并以此获得杂波谱中心的多普勒频率和空间频率,构造空时转换矩阵,使训练单元与待测单元的杂波分布趋于一致.研究表明,与常规角度多普勒补偿方法相比,该方法不受误差的影响,在存在误差时,可以获得更准确的杂波谱中心多普勒频率和空间频率,能够对杂波距离依赖性进行自适应补偿,且补偿性能更优.由于笔者使用稀疏恢复估计杂波空时谱,而稀疏恢复求解中存在着伪值较多、基失配（off-grid)等问题,因此如何减少或者消除伪值和基失配的影响,获得更加准确的杂波空时谱分布,是下一步工作的重点.

[1]Klemm R.The Applications of Space-time Adaptive Processing[M].London:IEE,2004.

[2]刘聪锋,廖桂生.基于Bayes准则的STAP协方差矩阵估计算法[J].西安电子科技大学学报,2008,35(2):41-45. Liu Congfeng,Liao Guisheng.Covariance Matrix Estimation for the STAP Based on the Bayes Criterion[J].Journal of Xidian University,2008,35(2):41-45.

[3]Carlson B D.Covariance Matrix Estimation Errors And Diagonal Loading In Adaptive Arrays[J].IEEE Transactions on Aerospace and Electronic Systems,1988,24(4):397-401.

[4]Wu J,Wang T,Meng X,et al.Clutter Suppression for Airborne Non-side Looking Radar Using EROE-STAP Algorithm[J].IET Radar,Sonar&Navigation,2010,4(4):497-506.

[5]Shen M,Meng X,Zhang L.Efficient Adaptive Approach for Airborne Radar Short-range Clutter Suppression[J].IET Radar,Sonar&Navigation,2012,6(9):900-904.

[6]Borsari G K.Mitigating Effects on STAP Processing Caused by an Inclined Array[C]//Proceedings of the IEEE National Radar Conference.Piscataway:IEEE,1998:135-140.

[7] 孟祥东,吴建新,王彤,等.机载双基雷达杂波分析及其距离模糊杂波的抑制[J].西安电子科技大学学报,2008,35 (6):42-48. Meng Xiangdong,Wu Jianxin,Wang Tong,et al.Clutter Analysis and Range-ambiguous Clutter Suppression for Bistatic Airborne Radar[J].Journal of Xidian University,2008,35(6):42-48.

[8]Friedlander B.The MVDR Beamformer for Circular Arrays[C]//Conference Record of the Asilomar Conference on Signals,Systems and Computers:1.Washington:IEEE Computer Society,2000:25-29.

[9]Lapierre F D,Droogenbroeck M V,Verly J G.New Methods for Handling the Range Dependence of the Clutter Spectrum in Non-side Looking Monostatic STAP Radars[C]//Proceedings of the IEEE International Conference on Acoustics,Speech and Signal Processing.Piscataway:IEEE,2003:73-76.

[10]Picciolo M L,Goldstein J S,Myrick W L.Compressive Sensing for Radar STAP[C]//Proceedings of the IEEE National Radar Conference.Piscataway:IEEE,2013:1-4.

[11]孙珂,张颢,李刚,等.基于杂波谱稀疏恢复的空时自适应处理[J].电子学报,2011,39(6):1389-1393. Sun Ke,Zhang Hao,Li Gang,et al.STAP via Sparse Recovery of Clutter Spectrum[J].Acta Electonica Sinica,2011,39(6):1389-1393.

[12]王俊华,黄知涛,周宇,等.基于近似l0范数的稳健稀疏重构算法[J].电子学报,2012,40(6):1185-1189. Wang Junhua,Huang Zhitao,Zhou Yu,et al.Robust Sparse Recovery Based on Approximate l0Nom[J].Acta Electonica Sinica,2012,40(6):1185-1189.

[13]Hu Chenxi,Liu Yimin,Li Gang,et al.Improved FOCUSS Method for Reconstruction of Cluster Structured Sparse Signals in Radar Imageing[J].Science China Information Science,2012,55(8):1776-1788.

[14]方红,杨海荣.贪婪算法与压缩传感理论[J].自动化学报,2011,37(12):1413-1421. Fang Hong,Yang Hairong.Greedy Algorithms and Compressed Sensing[J].Acta Automatica Sinica,2011,37(12): 1413-1421.

（编辑:郭 华)

Novel angle Doppler compensation method

FENG Weike1,ZH ANG Yongshun1,ZHANG Dan2
(1.Air and Missile Defense College,Air Force Engineering Univ.,Xi’an 710051,China; 2.School of Electronic Engineering,Xidian Univ.,Xi’an 710071,China)

In a non-side looking airborne radar system,the clutter of different range cells is not independently and identically distributed,which is caused by the severe clutter range-dependence.The clutter range-dependence can be compensated by the angle Doppler compensation(ADC)method simply and quickly.Although the ADC is widely applied,the compensation performance of the ADC is affected by the system error significantly because of the mismatch between Doppler frequency and spatial frequency.In this paper,a novel method to compensate the clutter range-dependence,namely ADC using sparse recovery (SR-ADC),is proposed.Firstly,the clutter spectral distribution estimation of the test cell and training cells are obtained by using sparse recovery.Then,the spatial frequencies and Doppler frequencies of the clutter spectrum center are determined.Finally,transform matrixes of different training cells are designed so that the clutter of training cells could be nearly stationary with respect to that of the test cell.Compared with the traditional angle Doppler compensation method,the proposed method improves greatly the compensation performance,especially that of main-lobe clutter.In addition,this method can also achieve good performance when the system error exists.

non-side looking airborne radar;clutter range-dependence;angle Doppler compensation; sparse recovery

TN959

A

1001-2400（2015)06-0158-06

10.3969/j.issn.1001-2400.2015.06.027

2014-07-31

时间:2015-03-13

国家自然科学基金资助项目（60372033)

冯为可（1992-),男,空军工程大学硕士研究生,E-mail:fengweike007@163.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20150313.1719.027.html