新型的精密时差测量技术

屈八一,张 蕊,张 鑫,宋焕生,冯兴乐,周 渭

(1.长安大学信息工程学院,陕西西安 710064；2.西安电子科技大学机电工程学院,陕西西安 710071)

新型的精密时差测量技术

屈八一1,张 蕊1,张 鑫1,宋焕生1,冯兴乐1,周 渭2

(1.长安大学信息工程学院,陕西西安 710064；2.西安电子科技大学机电工程学院,陕西西安 710071)

以实现对小于计数时钟1个周期的非周期性短时时间间隔的精确测量为目的,研究了将上述短时间间隔利用一定的电路转换成相应的周期性信号间的相位差,然后利用比相测量技术测得被测短时间间隔大小的方法,设计了基于环形振荡器和锁相技术的转换电路和具有优良线性和分辨率的相位差测试方案.新的测量技术的实验系统能实现对0～90 000 ps之间的被测信号的高精度测量,测量精度优于15 ps,系统的随机误差不超过20 ps.

时间量化;比相;皮秒;环形振荡器

时间间隔的高精度测量是时频测控领域的一个基本问题,它的应用非常广泛.对于周期性的时间间隔可通过多次测量取平均值或者利用对形成它们的周期性信号间相位差的测量来提高测量精度.典型的双混频时差测量系统已具有百飞秒量级的分辨率.但是对于非周期性时间间隔的测量,依据目前现有技术,典型的测量方法有量化延迟法、时间扩展法、游标法和时间电压转换法等,要取得10 ps量级的分辨率已经很难[1-5].针对非周期性信号的测量,随机噪声的干扰在测量结果中很难消除[6-8].但在周期性信号的比相测量过程中,由于它将鉴相器给出的相位差脉冲用低通滤波器转换成了一个直流电平,其本质上有一个平均的过程在里面,则随机噪声的干扰被大大减小,另外,电路的触发稳定性也更高.而在现实中,精密时间间隔测量时大量被测是非周期性的时间间隔.鉴于对周期性信号相位差测量的高精度和高分辨率特性,笔者研究了将非周期性的短时间间隔转换为周期性信号间的相位差,然后进行测量的高精度短时间间隔测量方案,该方案理论上能将对非周期时差信号的测量分辨率提高到皮秒（ps)量级.

1 新型系统的设计方案

新型系统的设计原理框图如图1所示,工作波形图如图2所示.图1中时间间隔的开始信号和结束信号,分别是由被测时间间隔的开始信号和结束信号经过两接口电路处理后获得的.在实际中,上述接口电路还将完成触发电平大小选择、触发沿的类型选择、被测信号输入极性和通道选择、阻抗匹配等多功能.设被测时间间隔为t,t1和t2分别为振荡器1和振荡器2的起振延迟,则两个振荡器输出信号的相位时差为t+t2-t1.采用环形振荡器来实现时间间隔的转换电路,主要原因是环形振荡器的起振延迟具有小且稳定的特性[9-11].设t3和t4分别为振荡器1和振荡器2后级的精密整形电路的延迟,则两比相信号的相位时差为t+ t2+t4-t1-t3.设比相信号的频率为f0,周期为T0,比相仪的满度电压为Um,相位时差为t+t2+t4-t1-t3时的稳态输出电压为U（t+t2+t4-t1-t3),根据比相仪的工作原理,则有

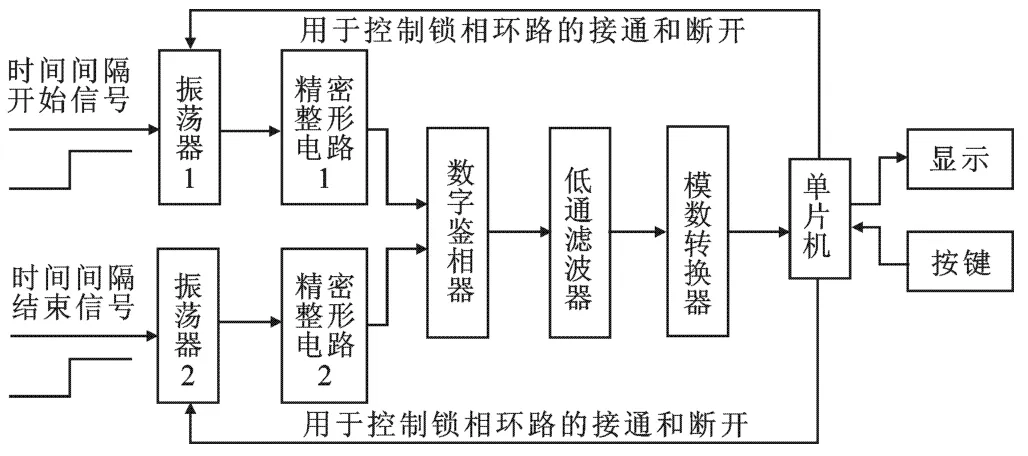
图1 系统原理框图

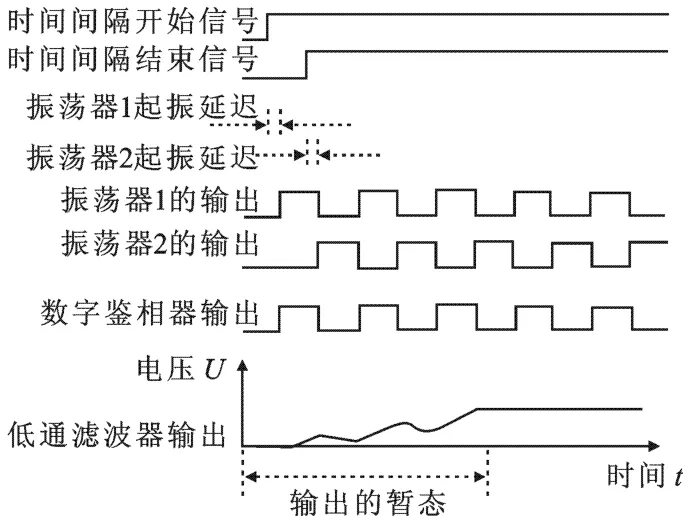
图2 系统工作波形图

由于式（1)中t1、t2、t3和t4的大小未知,通过式（1)无法根据输出电压U（t+t2+t4-t1-t3)求得被测时间间隔的大小t,因此,可通过校准测量的方法来解决该问题.假设校准测量时输入的被测时间间隔的大小为ta,两振荡器输出信号的相位时差为ta+t2+t4-t1-t3,低通滤波器的稳态输出电压为U（ta+t2+t4-t1-t3),则有

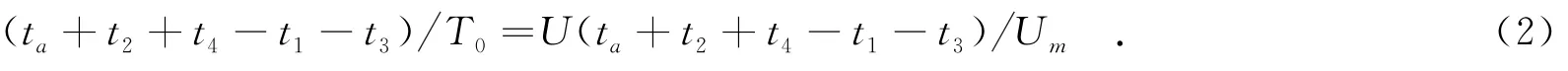
把式（1)减去式（2),可得

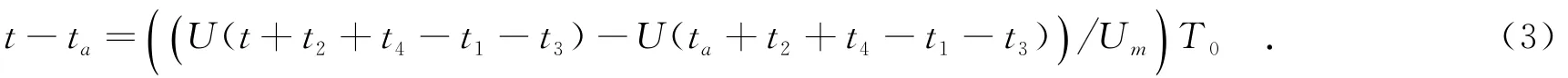
利用式（3),可在测得U（t+t2+t4-t1-t3)的情况下,求得被测时间间隔t.

对式（3)求全微分,可得

由式（4)可见,依据上述原理测量时,测量结果的精度与校准时的精度Δta、比相信号周期的精度ΔT0、比相电压的测量精度ΔU（t+t2+t4-t1-t3)及ΔU（ta+t2+t4-t1-t3)、比相满度电压的精度ΔUm等有关,系统的分辨率主要决定于比相电压测量时的分辨率.利用现有技术（例如直接数字式频率合成（DirectDigital Synthesis,DDS)移相技术)或利用精密相位微跃计,可产生精度优于1 ps的短时间间隔用于校准.由于两振荡器锁定到了基准源上,假设基准源的频率准确度为1×10-9,而比相信号是由振荡器输出分频获得的,因此有相同的频率准确度,设比相频率标称值为10 MHz,则上述比相信号周期的误差ΔT0= 1×10-16s.可见,以上两项误差在上述条件下可以忽略.ΔUm为满度电压的理论值和标称值之间的差异,它和数字鉴相器的供电电源的精度及稳定性有关.若是采用高性能的模数转换器（Analog-Digital Converter,ADC)来测量比相电压,测量精度与ADC的分辨率、电压基准源的精度及稳定性等有关.

2 主要电路的设计

2.1 转换电路的设计和实现

图3是转换电路的设计方案.控制信号是低电平时输出信号也是低电平,控制信号是高电平时将输出起始电平是高电平的方波信号,高电平的持续时间为tdelay1+tdelay2+tdelay3+tdelay,低电平的持续时间为tdelay1+ tdelay2+tdelay3+tdelay,则输出方波频率为

其中,tdelay1、tdelay2和tdelay3分别为图3中3个反相器的延迟; tdelay为与门的延迟、反馈导线的传输延迟及电路中除反相器外的分布参数引起的延迟之和.环形振荡器输出频率的稳定度上主要取决于延迟单元的稳定性[12-13].图3中在反馈环节放置一个高Q值的晶体谐振器来改善其输出的短期频率稳定度.

图3 环形振荡器的原理框图

2.2 基于锁相技术改善环形振荡器的频偏和频漂的设计

当利用环形振荡器来设计上述转换电路时,要求两振荡器的输出频率相同,可用锁相技术解决该问题,相关电路的设计参见文献[14].根据锁相技术的原理,环路滤波器是理想积分器的锁相环锁定时,两环形振荡器的输出信号是同频同相的,环路断开时加在环形振荡器上的电压不变,这样在短期内,两振荡器的频率可认为相等.设两振荡器标称频率都为f0,其日老化分别为K1和K2,则两振荡器在时刻t时的瞬时频率分别为

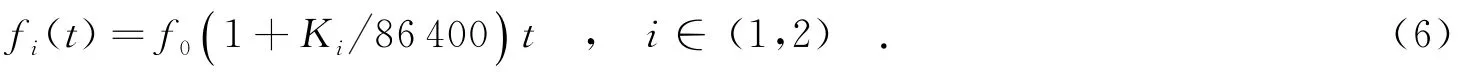
设TTIE1和TTIE2分别为振荡器1和振荡器2在1 s的累积时间误差,即

其中,ΔTi为振荡器1的第i个周期与振荡器1的标准周期之间的瞬时时差;N=1T0,为累积的周期个数,单位为ms,则有

设两振荡器在1s内的相对累积时间误差TTIE=TTIE1-TTIE2.两振荡器的日老化的最大值为K,则相对累积时间误差为

其中,f（t)为日老化为K,标称频率为f0的虚拟频率源的瞬时频率.由于频偏随着时间不断增加,因此,由式（9)可进一步得1 s内的相对累积时间误差,即

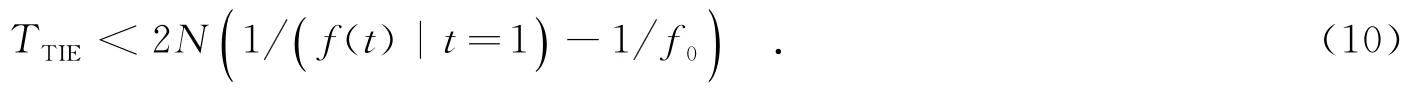
设f0=10 M Hz,K=10-3/日,代入式（10),可计算出t=1 ms时的累计时间误差TTIE＜2.3×10-14,可见,由于老化的时间很短,由老化引起的频偏可以忽略.

2.3 精密比相系统的设计和实现

由式（1)可见,在同样的电压分辨率条件下,高频比相的分辨率更高.但是高频比相时,非线性区所占比例增大.非线性是由于鉴相器反转时间的存在以及器件在0°或者360°附近时的误触发造成的.但鉴相器反转时间的存在并不影响系统在线性区的测量精度.目前数字鉴相器的速度高达几百兆赫兹以上,以此设计的比相系统的非线性区不到几纳秒.精密比相系统的原理框如图4所示.系统中两高速数字鉴相器在10 MHz进行鉴相,两个比相系统同时工作,即一个在非线性区时,另一个刚好在线性区.可通过对测量结果的分析,判断是否工作在线性区.在此基础上消除系统误差,进一步求出待测的短时间间隔的大小.在上述系统中,若需要实现对相位时差的1 ps的测量分辨率,设系统的工作电压为5 V,由式（4)可得,电压测量时的分辨率需优于50μV.目前用高分辨率的模数转换器能直接获得优于微伏量级的电压分辨率[10].实际中若采用买来的数据采集模块,则必须利用外部输入基准源,且基准源是数字鉴相器的供电电源.

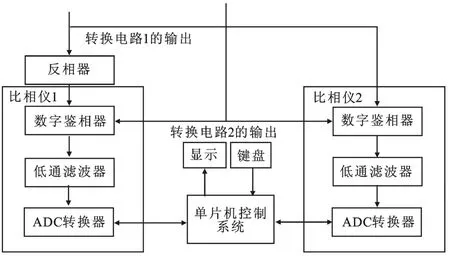
图4 精密比相系统的原理框图

3 实验结果和分析

对研制的转换电路进行了测试.测量仪器主要包括1个10 MHz的高稳参考信号源、Aglient DSO90254A多通道示波器和待测试的模块.锁定时,将10 MHz参考信号和两环形振荡器的输出分别加到示波器的3个通道上,通过波形图发现它们的频率是相同的,虽然两环形振荡器输出信号的过零点和参考信号比较存在抖动,但抖动大小一般不超过10 ps.可见,目前环形振荡器的短期稳定度仍较10 MHz参考源的稳定度差.失锁时,测试了环形振荡器在1 s内的累计时间误差（Time Interval Error,TIE)的大小.上述误差等于开始时两信号上升沿之间的差异和1 s之后两信号上升沿之间的差异的差值.经多次测量发现,上述TIE一般不超过15 ps.它主要是由环形振荡器的短期稳定度造成的,在测量过程中两环形振荡器的频漂造成的误差是可以忽略的.

基于比较法,对文中研制的精密相位测量模块进行了测试.选用的参考测量仪是Agilent的脉冲信号发生器81130A,它的两路输出信号的时差可以调节,分辨率为2 ps.81130A和比相系统中采用的参考频率源相同,参考频率源引入的误差可以忽略.利用81130A产生待测信号,不同输入条件下所得的测量数据如表1所示.表1中,A±B类型的数据的含义:A是10次测量结果的均值,B是测量结果的均方差值.以81130A显示的时差为被测的真值,以精密相位测量模块测得的时差为被测的测量值,用最小二乘法进行拟合,求得精密相位测量模块的零点偏差,并将其用于系统校准,校准后的数据如表2所示.由表2可见,经过校准后的相差测量模块的准确度很高,10次测量结果的均值的偏差不超过3 ps,基本测量范围可达0～90 000 ps,这个测量范围足以满足对正负1个字误差测量的量程要求,而在上述范围内的线性度达0.003%,非线性误差可以忽略.

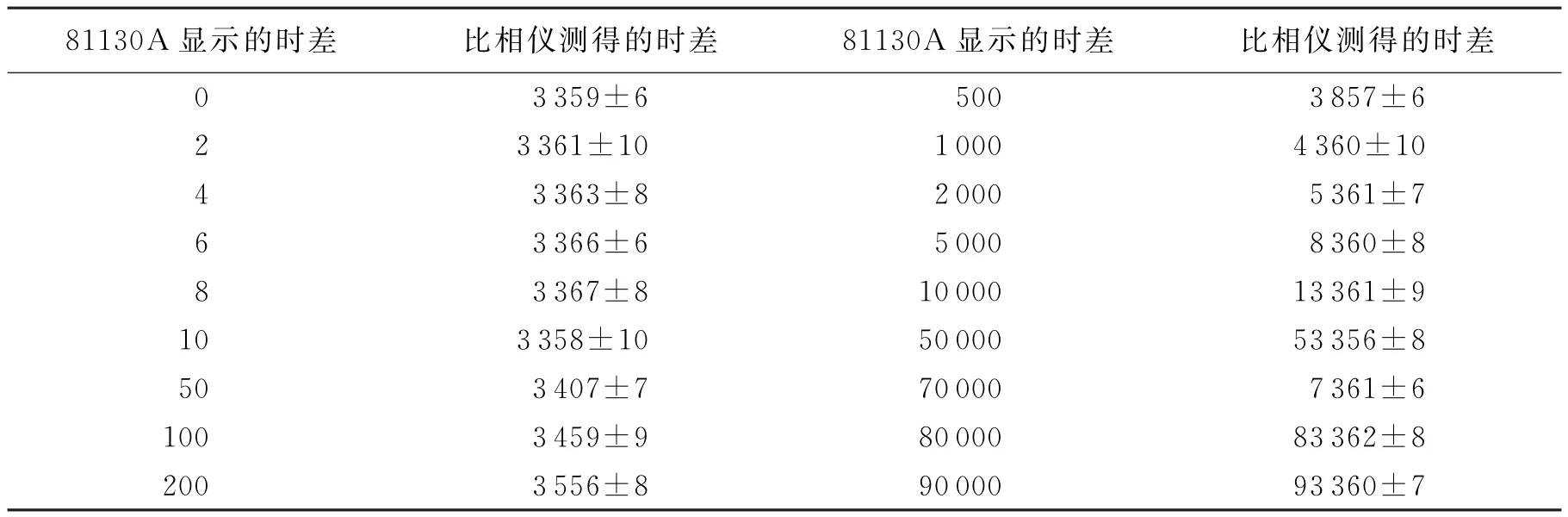
表1 比相仪没校准前的测量数据 ps

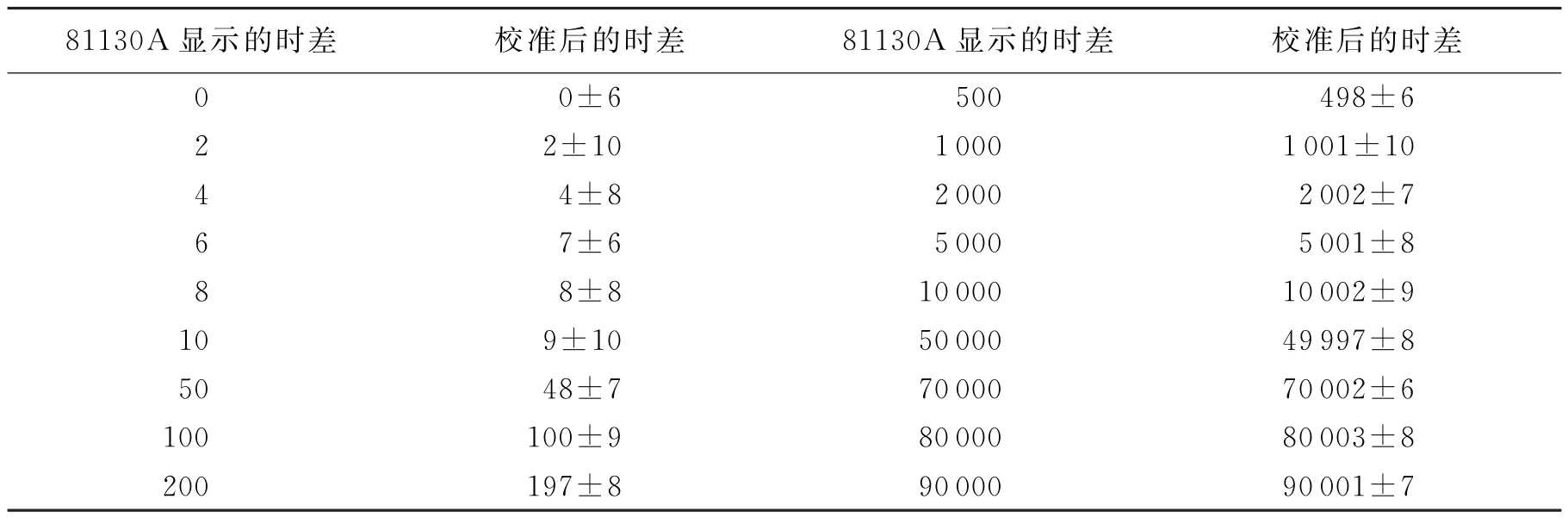
表2 比相仪校准后的数据 ps

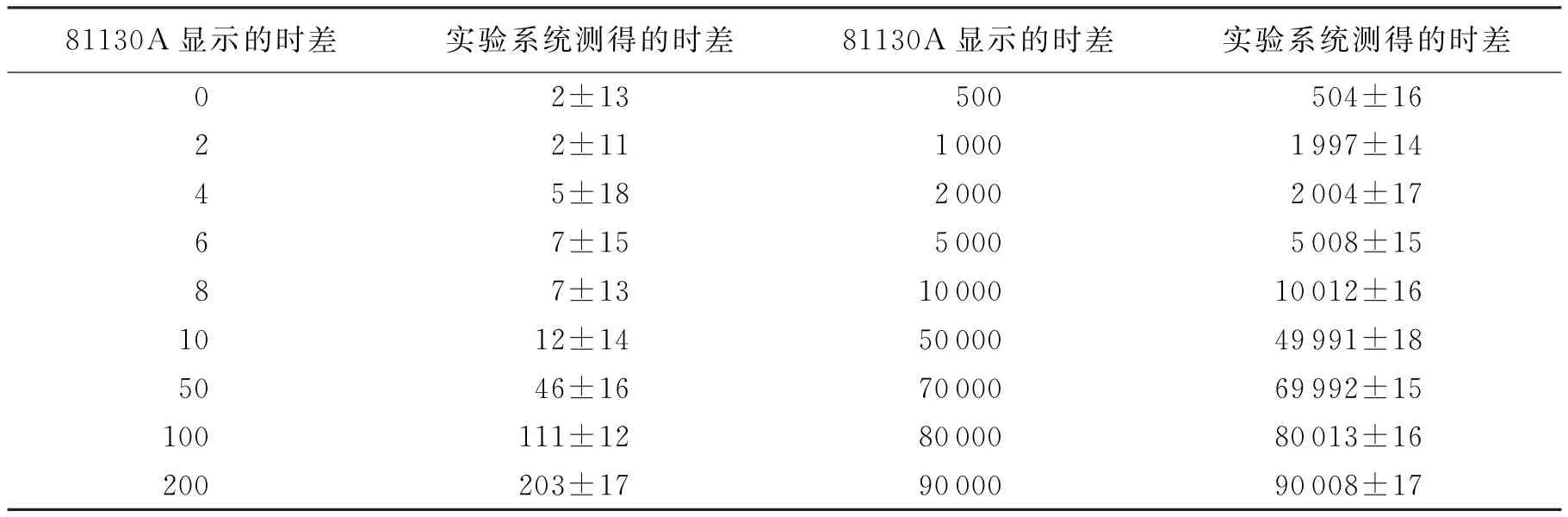
表3 实验系统的测试数据 ps

整个实验系统的测试方案与精密比相系统的测试方案相同,它在不同输入条件下的输出如表3所示.可见,经过校准后的测量系统能对0～90 000 ps之间的任意非周期时差进行高精度的测量,10次测量的均值精度优于15 ps,10次测量的均方差值优于20 ps,实验系统的线性度优于0.015%.测量结果的抖动属于随机误差,主要是由于转换电路引入的噪声和抖动、相位差测量模块引入的噪声和抖动、电路部分的噪声、电源的稳定性等造成的.优于20 ps的均方根误差说明了系统的稳定很高.

4 结束语

笔者针对非周期性短时间间隔的测量问题,采用了先将非周期性短时间间隔转换成周期性信号间的相位差,然后测量的方法,对上述问题进行了研究.完成了系统设计和各功能模块的研制,构建了实验系统,并对其进行了测试和分析.实验结果表明,上述方法针对短时间间隔能取得很好的性能.存在的问题是,系统存在结构复杂、调试困难的缺点.

[1]Zhao L,Hu X Y,Wang J H,et al.The Design of a 16-Channel 15 ps TDC Implemented in a 65 nm FPGA[J].IEEE Transactions on Nuclear Science,2013,60(5):3532-3536.

[2]Ugur C,Korcyl G,Michel J,et al.264 Channel TDC Platform Applying 65 Channel High Precision(7.2 psRMS) FPGA Based TDCs[C]//Proceedings of 2013 IEEE Nordic Mediterranean Workshop on Time to Digital Converters. Washington:IEEE Computer Society,2013:26-30.

[3]Chen Y H,Lu C W,Chang T Y,et al.A High Resolution FPGA-based TDC with Nonlinearity Calibration[C]// International Symposium on Instrumentation&Measurement,Sensor Network and Automation.Washington:IEEE Computer Society,2012:44-47.

[4]Lee S K,Seo Y H,Suh Y,et al.A 1 GHz ADPLL with a 1.25 ps Minimum-resolution Sub-exponent TDC in 0.18μm CMOS[C]//IEEE International Solid-state Circuits Conference Digest of Technical Papers.Washington:IEEE ComputerSociety,2010:482-483.

[5]Yao C Y,Hsia W C,Tsai P J,et al.The Vernier-Based TDC Employing Soft-Injection-Locked Ring Oscillators[C]// Proceedings of 2012 IEEE International Instrumentation and Measurement Technology Conference.Washington:IEEE Computer Society,2012:2291-2294.

[6]王海,周渭,刘畅生,等.一种新的短时间间隔测量方法[J].西安电子科技大学学报,2008,35(2):267-271. Wang Hai,Zhou Wei,Liu Changsheng,et al.Novel Short Time Interval Measurement Method[J].Journal of Xidian University,2008,35(2):267-271.

[7]屈八一,周渭,陈发喜,等.高精度时间间隔测量仪的研制[J].仪器仪表学报,2009,30(7):1476-1480. Qu Bayi,Zhou Wei,Chen Faxi,et al.Development of High Precision Time Interval Measurement Module[J].Chinese Journal of Scientific Instrument,2009,30(7):1476-1480.

[8]Moschitta A,Stefani F,Petri D.Measurements of Transient Phenomena with Digital Oscilloscopes[J].IEEE Transactions on Instrumentation and Measurement,2007,56(6):2486-2491.

[9]Jovanovic G,Stojcev M,Stamenkovic Z.A CMOS Voltage Controlled Ring Oscillator with Improved Frequency Stability [J].Scientific Publications of the State University of Novi Pazar Serial A:Applied Mathematics&Information and Mechanics,2010,2(1):1-9.

[10]Williams S,Thompson H,Hufford M,et al.An Improved CMOS Ring Oscillator PLL with Less than 4ps RMS Accumulated Jitter[C]//Proceedings of the IEEE Custom Integrated Circuits Conference.Piscataway:IEEE,2004:151-154.

[11]Kabbani A,Al-Khalili D,Al-Khalili A J.Technology-portable Analytical Model for DSM CMOS Inverter Transitiontime Estimation[J].IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems,2003,22(9): 1177-1187.

[12]白丽娜,周渭,惠新明,等.频率标准瞬态稳定度的精密测量[J].西安电子科技大学学报,2014,41(2):102-106. Bai Lina,Zhou Wei,Hui Xinming,et al.Precise Measurement of the Transient Stability of Frequency Standards[J]. Journal of Xidian University,2014,41(2):102-106.

[13]刘娅,李孝辉,王玉兰.一种基于数字技术的多通道频率测量系统[J].仪器仪表学报,2009,30(9):1963-1968. Liu Ya,Li Xiaohui,Wang Yulan.Multi-channel Frequency Measurement System Based on Digital Signal Processing[J]. Chinese Journal of Scientific Instrument,2009,30(9):1963-1968.

[14]屈八一,宋焕生,周渭,等.一种新型不同频直接鉴相的锁相环[J].西安电子科技大学学报,2014,41(2):208-215. Qu Bayi,Song Huansheng,Zhou Wei,et al.Novel Phase-locked Loop with Direct Phase Detection for Two Frequency Different Signals[J].Journal of Xidian University,2014,41(2):208-215.

（编辑:齐淑娟)

Novel short time interval measurement technology with high precision

QU Baiyi1,ZHANG Rui1,ZHANG Xin1,SONG Huansheng1,FENG Xingle1,ZHOU Wei2
(1.School of Information Engineering,Chang’an Univ.,Xi’an 710064,China; 2.School of Mechano-electronic Engineering,Xidian Univ.,Xi’an 710071,China)

To get a higher precision when measuring the short time interval which is less than the counting clock’s cycle and has a non-periodic characteristic,a novel short time interval measurement technology with high precision is expounded,in which the short time interval will be measured by converting the time interval into the corresponding phase differences between the periodic signals by particular circuits,and the measurement will be proceeded based on phase comparison measurement technology.The paper gives the conversion circuits based on ring oscillators and phase-locked-loop technology,as well as the designing method of the phase comparison device with fine linearity and resolution.The time interval between 0 to 90 ns can be measured by the current experimental system with an error of no more than 15 ps.Experimental results also show that the random error caused by the noise floor of the system is as low as 20 ps.

time digitalization;phase comparison;picoseconds;ring oscillator

TM935.15

A

1001-2400（2015)06-0152-06

10.3969/j.issn.1001-2400.2015.06.026

2014-06-30

时间:2015-03-13

陕西省工业攻关资助项目（2011K06-32);中央高校基本科研业务费专项资金资助项目（CHD2011TD012,CHD2010JC080);长安大学交通运输工程博士点基金资助项目（20120205110001);中国博士后基金资助项目（2013M530411);国家自然科学基金资助项目（60772135,10978017)

屈八一（1981-),男,副教授,博士,E-mail:404182049@qq.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20150313.1719.026.html