一种低快拍情况下的稳健自适应波束形成算法

朱玉堂,赵永波,水鹏朗,程增飞,李 慧

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

一种低快拍情况下的稳健自适应波束形成算法

朱玉堂,赵永波,水鹏朗,程增飞,李 慧

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

针对低快拍情况下自适应波束形成器性能急剧下降的问题,提出一种基于联合协方差矩阵修正和导向矢量估计的稳健自适应波束形成算法.该算法先对协方差矩阵进行修正,再用修正的协方差矩阵估计最优导向矢量,最后利用修正的协方差矩阵和估计的最优导向矢量计算自适应波束形成器的加权矢量.该算法不仅能有效地处理各种失配,还能解决自适应波束形成器在低快拍情况下性能急剧下降的问题,提高了自适应波束形成器的稳健性.计算机仿真验证了所提算法的正确性和有效性.

自适应波束形成;阵列信号;低快拍;稳健性

自适应波束形成是阵列信号处理中一个重要的研究方向,在雷达、声纳、无线通信、医学影像和射电天文学等多种领域具有广泛的应用.在理想情况下,自适应波束形成器具有较高的分辨力和较强的干扰抑制能力.但在实际工程应用中,快拍数有限、期望信号指向误差、阵列标定误差或局部相干散射等非理想因素均可引起协方差矩阵失配和导向矢量失配,导致主瓣畸变、旁瓣升高和期望信号自消,造成自适应波束形成器的性能下降.如果接收数据中存在期望信号,自适应波束形成器的性能下降更严重.因此,稳健性成为了自适应波束形成器的必需要求.

为提高自适应波束形成器的稳健性,近年来学者们提出了很多稳健自适应波束形成算法,如基于特征空间的算法[1],常用的对角加载类算法[2-5]和基于角度区间类算法[6-7]等.其中基于特征空间的算法利用假定的导向矢量在信号协方差矩阵的特征空间中投影,缓解了导向矢量失配对波束形成器性能的影响;对角加载类算法通过向协方差矩阵添加加载阵,提高了波束形成器对一般失配的稳健性;基于角度区间类算法利用期望信号所在的角度区间估计期望信号的最优导向矢量,也同样增强了波束形成器对一般失配的稳健性.然而这些算法在低快拍情况下性能急剧下降,甚至部分算法在快拍数低于阵元数情况下完全失效.快拍数是信号处理中一种重要资源,高的快拍数可以提高系统的稳定性,但也会造成计算复杂度增高、硬件实现困难、通信及时性差等一系列问题.另外,当接收数据的维数比较大（如多输入多输出（Multiple Input Multiple Output,MIMO)雷达)或者要求自适应波束形成器对接收环境的快速变化反应敏感时,接收数据的采样快拍数都不会很高[8].因此,如何在低快拍情况下改善自适应波束形成器的稳健性具有重要意义.

针对低快拍情况下自适应波束形成器的稳健性问题,笔者在深入分析低采样快拍数对自适应波束形成器性能影响的基础上,提出一种基于联合协方差矩阵修正和期望信号最优导向矢量估计的稳健波束形成算法.与现有的算法相比,文中算法对各种失配都具有较好的稳健性,特别是在快拍数低于阵元数的情况下.

1 信号模型

考虑一个N元的线阵,有一个远场窄带期望信号和P个远场干扰信号入射到阵列,其中P+1＜N,则第k次快拍阵列的接收数据矢量可以表示为

其中,xs（k)、xi（k)和xn（k)分别为接收数据中互不相关的期望信号、干扰和噪声部分,xs（k)=a s（k),a∈CN×1,为期望信号对应的导向矢量,s（k)为期望信号的复包络.

对接收数据进行波束形成,则波束形成器的输出为其中,w=[w1,w2,…,wN]T∈CN,为波束形成器的加权矢量,（·)T和（·)H分别表示转置和共轭转置.

阵列的输出信干噪比为

为期望信号的功率,Ri+n=E{[ xi（k)+xn（k)][xi（k)+xn（k)]H}∈CN×N,为干扰噪声协方差矩阵,E{·}表示数学期望.其中,

2 MVDR和MPDR

波束形成器的最优加权矢量可以通过最大化阵列的输出信干噪比得到,其等价的数学模型[9]可以表示为

小方差无畸变响应（Minimum Variance Distortionless Response,MVDR)波束形成器,式（5)的解w2=被称为最小能量无畸变响应（Minimum Power Distorionless Response,MPDR)波束形成器.尽管在理想条件下两种波束形成器等价相同,但在低采样快拍数情况下MPDR波束形成器的性能远不如MVDR波束形成器.

假定接收数据为L次快拍的采样数据,期望信号、干扰和噪声之间以及它们相互间的相关性增加,互不相关的假设不再满足,则

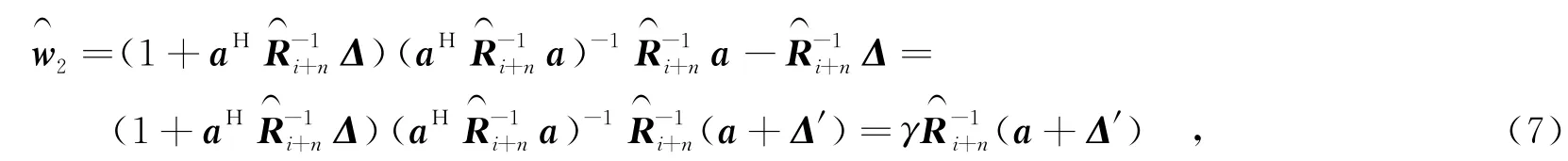
3 文中算法

文献[1]证明了由快拍数不足造成的协方差矩阵失配可以和期望信号的导向矢量失配等价,因此,可以通过修正︵w2中的期望信号导向矢量或协方差矩阵来同时克服快拍数不足和导向矢量失配对SMI（也就是MPDR[9])波束形成器性能的影响.但是这种等价关系是建立在期望信号的功率远大于噪声功率且快拍数远高于阵元数的条件之上,如果该条件不满足,特别是快拍数高于阵元数时,单一地修正协方差矩阵或期望信号导向矢量并不能很好地解决上述失配问题.因此,笔者提出一种新的稳健自适应波束形成算法,将协方差矩阵的修正和期望信号最优导向矢量的估计联合起来,从而更好地处理波束形成器的协方差矩阵失配和导向矢量失配.

3.1 协方差矩阵的修正

在低快拍情况下采样协方差矩阵的失配主要表现为小特征值的扩散,下面将通过公式推导来说明这个问题,并提出解决方法.

将︵Rx特征分解为

其中,λk（k=1,…,P)为干扰对应的特征值,λP+1为期望信号对应的特征值,λk（k=P+2,…,N)为噪声对应的小特征值,uk为特征值λk对应的特征向量.由于x为Hermitian矩阵,因此,所有特征值都是实数且特征向量相互正交.

取最小特征值为λmin,则x的逆可用特征值和特征向量表示为

从上式可以看出,自适应波束图可以认为是静态波束图（即没有外界干扰仅有内部噪声时的状态)减去特征向量对应的特征波束图,a即为静态波束图对应的权值.由于干扰的功率远大于噪声的功率,所以（λkλmin)λk（i=1,…,P)接近1,干扰几乎被完全抑制掉,在干扰方向形成零陷;而期望信号由于受到约束的保障,在导向矢量不存在失配的情况下,能够无损耗地输出.在假设的理想条件下用协方差矩阵Rx计算时,λP+1=…=λN=λmin,（λk-λmin)λk=0（k=P+2,…,N),小特征值对应的特征矢量不参与计算.但在低快拍情况下,期望信号、干扰和噪声之间以及它们相互间的相关性增加.假设的白噪声实际等价为色噪声,从而造成了采样协方差矩阵的小特征值扩散[10].小特征值对应的特征矢量扰动参与了自适应权值的计算,导致了自适应波束形成器的主瓣畸变,旁瓣抬高,干扰对应的零陷变浅,收敛速度变慢,甚至发散.另外,当快拍数低于阵元数时,部分小特征值等于0,传统的MPDR波束形成器完全失效.

为了解决低快拍数造成采样协方差矩阵小特征值扩散的问题,文中采用自动对角加载的方法对x进行修正[11].基本思想是通过单位阵I和采样协方差矩阵Rx的凸线性组合来估计协方差矩阵,即

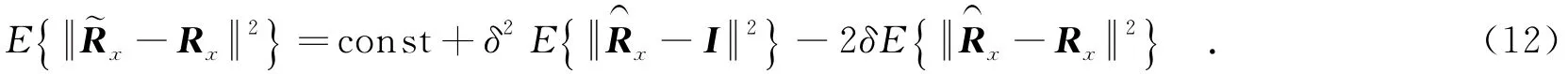
这样最小化,就可以得到

要计算出MVDR波束形成器的权值,就必须得到干扰噪声协方差矩阵.干扰噪声协方差矩阵的估计方法有很多[7,12-13],为了方便说明问题,利用Capon谱重构干扰噪声协方差矩阵[7]为

3.2 期望信号最优导向矢量的估计

根据上文的分析,在低快拍情况下单一地修正协方差矩阵并不能彻底地解决期望信号的导向矢量失配,还需要自适应地估计期望信号的最优导向矢量.期望信号导向矢量的估计可以转化为导向矢量误差e的估计,而导向矢量误差e又可以分解为垂直部分e⊥（与期望信号的假定导向矢量a垂直)和平行部分e∥（与a平行),其中e∥不影响阵列的输出信干噪比.因此,类似于文献[7]期望信号最优导向矢量的估计可以简化为垂直部分e⊥的搜索:

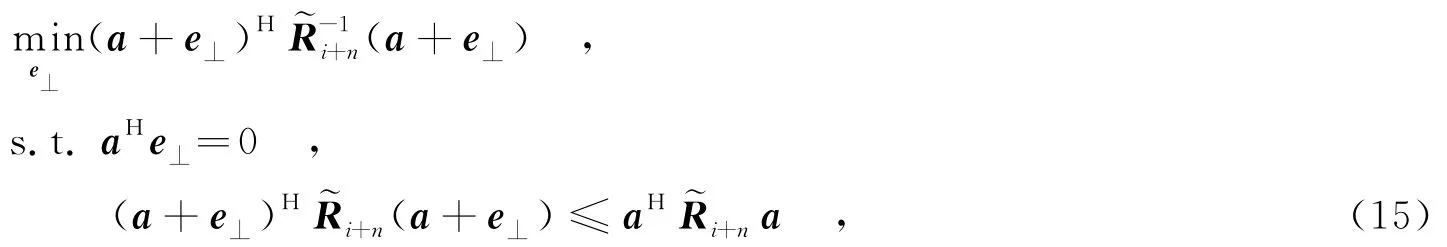
其中,目标函数是为了最大化阵列的输出功率,第1行约束是为了保证e⊥和假定导向矢量a垂直,第2行约束是为了防止a+e⊥向干扰导向矢量及其线性组合收敛.又因为i+n正定,所以这个优化问题是一个可解的二次约束二次问题（Quadratic Constraint Quadratic Problem,QCQP).求解之后就可以得到期望信号最优导向矢量的估计为

在得到重构的干扰噪声协方差矩阵和估计的最优导向矢量后,将其分别代入MVDR波束形成器就可以得到一种新的稳健自适应波束形成器:

4 计算机仿真

为了验证文中算法的有效性,进行如下仿真.仿真基于一个N=10的均匀线阵,阵元间隔为半波长,接收数据中包含互不相关的期望信号、干扰和噪声,期望信号的方向为5°,干扰信号的方向分别为30°和50°,信噪比（Signal to Noise Ratio,SNR)为10 dB,干噪比（Interference and Noise Ratio,INR)均为30 dB,噪声为空域、时域独立的零均值圆对称复高斯白噪声.另外,为了充分说明文中算法的性能,在部分仿真中,文中算法与LSMI[2]、WC-RCB[3]、GLC[4]、文献[6-7]的算法进行对比,其中LSMI的对角加载因子设定为10倍的噪声功率,WC-RCB的不确定集上界设定为0.3,文中算法、文献[6-7]的算法中期望信号所在的角度区间设定为Θ=[0°,10°],干扰信号所在的角度区间为Θ的补集.

实验1 在低快拍情况下MVDR和MPDR的关系.接收数据的快拍数L=20,其他参数根据上文设定.

图1 MVDR和MPDR的波束响应

实验2 自动对角加载对小特征值扩散的改善.接收数据的快拍数L=5,蒙特卡洛试验次数为500,其他参数根据上文设定.

从图2中可以看出,由于接收数据的快拍数过少,采样协方差矩阵的小特征值远小于理想协方差矩阵的小特征值,但是经过自动对角加载的处理,修正后采样协方差矩阵的小特征值逼近理想协方差矩阵的小特征值.另外,从图2中还可以看出,修正后协方差矩阵仍然存在失配,说明了采用MVDR波束形成器的必要性.

实验3 在低快拍情况下不同算法的波束响应对比.接收数据的快拍数L=5,其他参数根据上文设定.

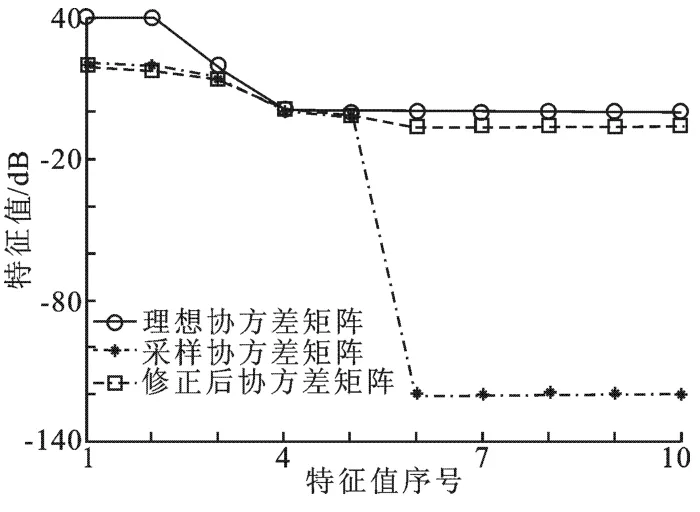
图2 不同协方差矩阵的特征值分布

图3 给出了在低快拍情况下,文中算法与适合低快拍的常用算法（LSMI、GLC、WC-RCB)的波束响应的对比,从图中可以看出,文中算法不仅可以保证主瓣的形状、压低旁瓣,还能在干扰方向形成很深的零陷.

实验4 在导向矢量失配情况下不同算法的性能对比.在存在指向误差的情况下期望信号的假定方向为2°,在存在近场相干散射的情况下期望信号的实际导向矢量可以表示为=a0+,a0为直达信号的导向矢量,d（θi)（i=1,…,I)表示从θi方向入射的相干散射信号对应的导向矢量,ϕi为相干散射信号相对直达波信号的相位差.此例中I取4,直达波信号的入射方向为0°,反射信号的入射方向θi服从均值为0°,标准差为4°的高斯随机分布,ϕi服从[0,2π]间的均匀分布.蒙特卡洛试验次数为500,其他参数根据上文设定.

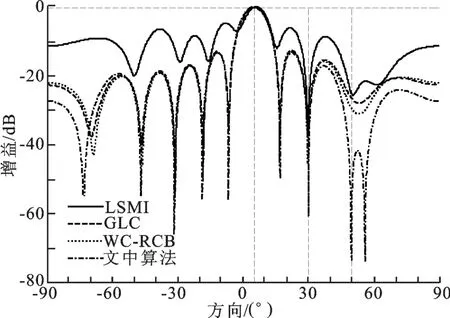
图3 文中算法与常用算法的波束响应对比

图4（a)和图4（b)分别给出了期望信号存在指向误差和近场相干散射情况下不同算法的性能对比.从图中可以看出,当快拍数低于阵元数时,文中算法的性能明显优于其他算法;当快拍数高于阵元数时,文中算法的性能和同类算法相当.另外,从图中还可以看出,MVDR类算法（文中算法和文献[7]算法)的性能优于MPDR类算法（LSMI、GLC、WC-RCB和文献[6]算法);单一地修正协方差矩阵失配的算法（LSMI、GLC和WC-RCB)或导向矢量失配的算法（文献[6-7]算法)的性能均不如联合修正协方差矩阵失配和导向矢量失配的文中算法,特别是在快拍数低于阵元数情况下.

图4 在导向矢量存在失配时不同算法的性能对比

5 结束语

针对低快拍情况下自适应波束形成器性能急剧下降的问题,提出一种新的稳健波束形成算法.该算法基于MVDR波束形成器,联合协方差矩阵的修正和期望信号导向矢量的估计,提高了阵列的输出信干噪比（Signal to Interference and Noise Ratio,SINR),增强了算法对协方差矩阵失配和导向矢量失配的稳健性.

[1]Feldmanand D D,Griffiths L J.A Projection Approach for Robust Adaptive Beamforming[J].IEEE Transactions on Signal Processing,1994,42(4):867-876.

[2]Cox H,Zeskind R M,Owen M M.Robust Adaptive Beamforming[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1987,35(10):1365-1375.

[3]Vorobyov S A,Gershman A B,Luo Z Q.Robust Adaptive Beamforming Using Worst-case Performance Optimization: a Solution to t The Signal Mismatch Problem[J].IEEE Transactions on Signal Processing,2003,51(2):313-324.

[4]Du L,Li J,Stoica P.Fully Automatic Computation of Diagonal Loading Levels for Robust Adaptive Beamforming[J]. IEEE Transactions on Aerospace and Electronic Systems,2010,46(1):449-458.

[5] 刘聪峰,廖桂生.最差性能最优的稳健波束形成算法[J].西安电子科技大学学报,2010,37(1):1-8. Liu Congfeng,Liao Guisheng.Robust Beamforming Algorithm Using Worst-case Performance Optimization[J]. Journal of Xidian University,2010,37(1):1-8.

[6]Khabbazibasmenj A,Vorobyov S A,Hassanien A.Robust Adaptive Beamforming Based on Steering Vector Estimation with as Little as Possible Prior Information[J].IEEE Transactions on Signal Processing,2012,60(6):2974-2987.

[7]Gu Y J,Leshem A.Robust Adaptive Beamforming Based on Interference Covariance Matrix Reconstruction and Steering Vector Estimation[J].IEEE Transactions on Signal Processing,2012,60(7):3881-3885.

[8]Chao K W,Chen J C,Ting P.A Shrinkage Linear Minimum Mean Square Error Estimator[J].IEEE Signal Processing Letters,2013,20(12):1179-1182.

[9]Van Trees H L.Optimum Array Processing[M].New York:Wiley,2002.

[10]Carlson B D.Covariance Matrix Estimation Errors and Diagonal Loading in Adaptive Arrays[J].IEEE Transactions on Aerospace and Electronic Systems,1988,24(4):397-401.

[11]Stoica P,Li J,Zhu X,et al.On Using a Priori Knowledge in Space-time Adaptive Processing[J].IEEE Transactions on Signal Processing,2008,56(6):2598-2602.

[12]Rahmani M,Bastani M H,Shahraini S.Two Layers Beamforming Robust Against Direction-of-arrival Mismatch[J]. IET Signal Processing,2014,8(1):49-58.

[13]Yang T,Su T,Zhu W T,et al.Robust Adaptive Beamforming Using Beamspace Steering Vector Estimation[J]. Electronics Letters,2013,49(19):1201-1203.

（编辑:李恩科)

Robust adaptive beamforming algorithm in the situation of limited snapshots

ZHU Yutang,ZHAO Yongbo,SHUI Penglang,CHENG Zengfei,LI Hui
(National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)

In order to solve the problem of the sharp degradation of the adaptive beamformer performance due to limited snapshots,this paper proposes a new robust adaptive beamforming algorithm based on the correction of the covariance matrix and the estimation of the steering vector.The proposed algorithm first corrects the covariance matrix,and then obtains the estimation of the optimal steering vector with the corrected covariance matrix.Finally,using the corrected covariance matrix and the estimated optimal steering vector,the weight vector of the adaptive beamformer is calculated.The proposed algorithm can not only deal with all kinds of mismatches efficiently,but also solve the problem of the sharp degradation of the adaptive beamformer performance in the situation of limited snapshots,so that the robustness of the adaptive beamformer can be improved.Simulation results demonstrate the correctness and effectiveness of the proposed algorithm.

adaptive beamforming;array signal;limited snapshots;robustness

TN911.7

A

1001-2400（2015)06-0037-06

10.3969/j.issn.1001-2400.2015.06.007

2014-06-23

时间:2015-03-13

中央高校基本科研业务费专项资金资助项目（K5051202047)

朱玉堂（1988-),男,西安电子科技大学博士研究生,E-mail:yutangzhu_xd@163.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20150313.1719.007.html