平面应变试验与常规三轴试验条件下含细粒土砂力学特性比较研究

唐洪祥，张丽娟

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连116023)

实际工程中我们遇到的很多工程问题，例如路堤、隧道等可以看为平面应变问题，其稳定性、变形等的求解宜在ε2=0的条件下进行。常规三轴试验得到的本构参数来自于试验中特定的轴对称加载路径与边界条件，其对平面应变条件下的适应性值得怀疑，因而国内外一些学者进行了平面应变条件下土的应力应变关系的试验方面的研究:Lade等[1]对不同种类的砂土进行了平面应变试验，对平面应变条件下的的砂土的应力－应变关系特性进行了研究;Alshbil等[2]对三种颗粒粒径不相同的砂进行了平面应变试验，发现相同围压下密实的砂土试样在平面应变试验条件下比在常规三轴试验条件下有更高的强度，但相应的应变比常规三轴要小;Finno等[3]研究了颗粒级配良好的饱和松砂在平面应变试验不排水条件下的变形特性，试验结果发现应力－应变曲线在剪切带形成之前反映均匀应力和应变关系，之后试样软化表现出来的是有关土体的整体宏观平均力学行为;Alshbi等[4]对砂土进行平面应变试验，指出平面应变试验的应力－应变关系取决于围压和密度，而软化程度则取决于围压;Hayano等[5]研发了一套能进行局部应变测试的平面应变仪，并进行了多组试验来评价软岩的小应变变形特性;李广信等[6]对砂土平面应变的压缩性状进行了研究;张启辉等[7]将真三轴仪改进为平面应变仪，选取黏土为试验对象，对其进行了平面应变试验，通过图像采集可以得到试验过程中剪切带的形成的整个过程;宋新江等[8]对水泥土进行了平面应变试验，同时为了对比，也进行了同样试验条件下的三轴压缩试验，研究了其应力特性;邱成春等[9]对加筋砂进行了不同围压下的平面应变试验，得出了其在平面应变条件下剪切破坏时的强度公式;陈欧等[10]对砾石土分别进行常规三轴试验和平面应变试验，认为平面应变下的土的强度指标稍高于常规三轴试验的强度指标;马险峰等[11]对平面应变仪进行了改进，对砂土在平面应变条件下的特性进行了分析，同时推导了平面应变与常规三轴条件下砂土的强度参数的换算关系，使其可以用于工程实践;董建国等[12]对原状黏土进行了固结不排水平面应变试验，得出在试验过程中应力－应变曲线都体现出软化特征，并且具有明显的残余强度阶段，但这段并不能作为试样本身的强度。

一直以来学者们在不断努力，以期能够研发出新的仪器、新的技术以便研究土在平面应变条件下的特性。大连理工大学邵龙潭教授等[13]通过多年的研究和实践，对传统的土工三轴试验中的数字图像测量技术进行改进，并把改进后的测量系统应用于平面应变仪。

本文利用新型平面应变仪并结合数字图像测量技术，对某港口工程堤坝地基的含细粒土砂进行平面应变试验，研究该土料在平面应变条件下的应力应变特性;同时，通过与常规三轴试验结果的对比，分析了该土料在平面应变和常规三轴压缩条件下的变形与强度特征的差异，以期为同类工程问题提供参考。

1 试验土料、仪器及试验方法

1.1 试验土料

试验用土料来自于某港口工程堤坝地基的含细粒土砂，在实际工程中土料处于天然风干状态，故所取土料均为天然风干状态。在试验过程中控制试样相对密实度为60%，其主要的物理性质指标如表1所示。

表1 含细粒土砂的主要物理性质指标

1.2 平面应变仪简介

1.2.1 平面应变仪的概况

试验所用仪器为新型平面应变仪，其特点是:大小主应力均由程序控制加载，小主应力σ3采用了柔性加载的方式，数字图像测量在平面应变试验过程中可以保持对试样的全表面观测，这样可以更好的模拟试样的变形状态。试验中只需试验人员制备试样和输入试验参数即可，其余试验工作由程序控制完成。新型平面应变仪主要由压力室、加载系统、控制系统以及数字图像测量系统几部分组成。

1.2.2 平面应变仪各个主应力加载方式

平面应变仪的加载主要包括两部分:竖向大主应力的加载和侧向围压的加载。对于大主应力的加载实现的方式是通过横梁上的加载帽组件向下移动，与压力室接触后施加上去的。在施加大主应力的同时带有水囊的侧向挡板与后挡板以及钢化玻璃共同组成了压力室的内腔，通过向柔性水囊内注水来实现对小主应力的加载。

1.2.3 平面应变仪的测量系统

新型平面应变仪的测量系统是由CMOS摄像机、计算机图像处理软件以及计算机组成，先是摄像机将拍摄到的图片信息，传输到电脑中，然后图像处理软件进行处理。新型平面应变仪的数字图像测量系统对轴向变形采用非接触式测量，和传统测试方法相比，对试样扰动小，而且在试验过程中，数字图像摄像机拍摄设置的拍摄间隔比较小，拍摄完成的图片会自动保存到指定文件夹中，这样方便对变形及剪切带等问题研究。

试验过程中，CMOS摄像机会采集每个白色正方形的四个角点，也就是一共采集到32个正方形的128个角点进行分析，系统设置一定的采样时间间隔，局部应变可以通过分析系统跟踪的各个角点的位移得到，同时可以用Surfer软件绘出对应时刻对应各个角点应变等值线图。

1.3 含细粒土砂平面应变试验

1.3.1 试验方案

将含细粒土砂分别制作成平面应变试样和三轴压缩试样，其中平面应变试样尺寸为100 mm×100 mm×60 mm，对制备的试样分别进行固结围压为50 kPa、100 kPa、150 kPa的平面应变固结排水试验和常规三轴固结排水剪试验。

1.3.2 试验步骤

(1)试样安装。把制作好的试样放置到压力室底板上，并用六角螺钉固定。

(2)安装压力室。安装侧向水囊，注意检查水囊是否漏水;然后安装并固定钢化玻璃视窗组件，为了减小摩擦，一般会在透视窗上擦上一层润滑油。

(3)试样饱和。打开电脑控制程序和水囊开关，使水囊中充入一些水，确保撤去负压后试样不坍塌，这时围压保持在20 kPa左右;然后关闭负压，打开底部排水阀以及试样帽上排水阀，通过快速接头向试样内部通20 min左右的CO2;撤掉CO2，通无气水达到试样体积的2～3倍，然后关闭排水阀。

(4)试样固结。通过侧向水囊施加侧向围压，打开排水阀和压差传感器，试样开始固结。

(5)开始试验。打开数字图像测量软件，输入所需的参数，然后打开孔压传感器，横梁向下移动轴向荷载，试验开始。

(6)试验结束。当轴向应变达到15%后，试验结束，卸去围压和轴向压力，然后拆试样，关掉仪器，整理试验器材。

2 中主应力的求取

定义平面应变条件下的三个主应力方向为a，b，c，其中b为完全侧限方向，a的方向为大主应力方向，c为初始围压施加方向，且σc为初始围压且在试验中保持不变[14]。假定应力应变关系服从广义虎克定律，根据一般三维情况下的应力应变关系，令dεb=0，可以得到平面应变条件下应力和应变具有以下关系:

公式中已知 dσa、dσc、dεa、dεc，由式(3)即可求得dσb。从计算结果可以看出 σb开始是小于 σc的，随着试验的进行，σb逐渐增大，最后大于σc，也就是说试验过程中，小主应力σ3是变化的，在压缩过程的前期，前挡板方向的σb将是小主应力，随着试验的进行，σb逐渐增大直至大于σc，σb成为中主应力。由此方法求得三组不同围压下的中主应力。

3 含细粒土砂的平面应变试验与三轴试验结果对比分析

3.1 主应力差和大主应变之间的关系

图1给出了当围压分别为50 kPa、100 kPa、150 kPa时，相对密实度为60%的含细粒土砂平面应变试验和常规三轴压缩试验得到的大主应力差与大主应变的关系曲线。其中CTC代表常规三轴压缩试验，PSC代表平面应变试验。

图1 平面应变试验和常规三轴压缩试验大小主应力差与大主应变关系

从图1中可以看出，在到达大主应力差最大值之前，不论是常规三轴压缩试验还是平面应变试验，试样的大主应力差(σ1－σ3)都是随着大主应变增加而增加，应力－应变关系曲线呈直线增长。随着剪切的继续，大主应变逐渐增加，从图1中可以看出，相同围压下，平面应变试验的关系曲线位于常规三轴压缩试验曲线之上，也就是说在相同的大主应变下，平面应变试验的偏差应力大于常规三轴压缩试验，并且大主应变越大，这种现象越明显。

图2给出了当围压分别为50 kPa、100 kPa、150 kPa时，含细粒土砂平面应变试验的(σ2－σ3)～ε1关系曲线。对于常规三轴试验，σ2－σ3始终等于0，所以在图中没有显示。

从图2中可以看出在平面应变试验中，中小主应力差(σ2－σ3)是先减小至接近0然后再增大，之后的曲线趋势则跟大主应力差和大主应变关系曲线相似。之所以出现这种情况是因为中主应力求取过程中，以50 kPa为例，在试验开始阶段，前挡板方向的应力σb小于50 kPa，理论上也就是小主应力σ3;而侧向水囊方向为50 kPa，即为中主应力，在试验过程中，前挡板方向的应力σb逐渐增大，在达到σc之前，都属小主应力，所以在这个阶段小主应力是变化的。在较小的应变范围内，中小主应力差(σ2－σ3)为50－σ3，随着试验的进行，σb增大至50 kPa，此后前挡板方向的应力σb为中主应力，则中小主应力差变为σ2－50，即为图2所示的曲线趋势。

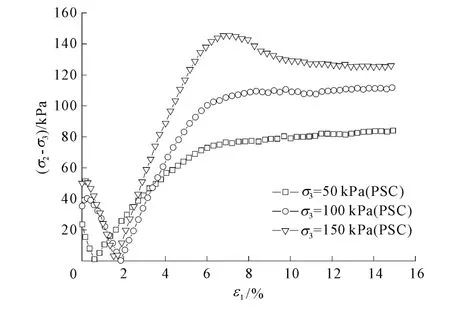
图2 平面应变试验中小主应力差－大主应变关系

3.2 广义剪应力和广义剪应变之间的关系

图3 给出了当围压分别为50 kPa、100 kPa、150 kPa时，含细粒土砂平面应变试验和常规三轴压缩试验得到的广义剪应变和广义剪应力变之间的关系曲线。纵坐标q为广义剪应力，横坐标是广义剪应变εs。其中:

从图3可以看出，在试验进行初始阶段，不同围压下广义剪应力随广义剪应变增加而增大，到剪应变达到一定值以后，应力—应变关系曲线都表现出明显的应变软化。另外也可以看出，围压相同的情况下，平面应变试验得到的曲线比常规三轴压缩试验更接近纵轴，表明在剪应变一样的情况下，平面应变试验得到的广义剪应力大于常规三轴压缩试验得到的，并且剪应变越大，这种现象越明显。

3.3 小主应变和大主应变之间的关系

图4给出了当围压分别为50 kPa、100 kPa、150 kPa时，含细粒土砂平面应变试验和常规三轴压缩试验得到的小主应变ε3和大主应变ε1之间的曲线关系。规定膨胀为负值，压缩为正值。其中常规三轴压缩试验中，ε1和 εv已知，由 εv=ε1+ε2+ε3及ε2= ε3，可以求出 ε3。

图3 平面应变试验和常规三轴压缩试验广义剪应力和广义剪应变关系

图4 平面应变试验和常规三轴压缩试验大小主应变之间的关系

从图4中可以看出，小主应变一直是负值，也就是说，在试验过程中，试样水平方向一直是膨胀的。另外从图4中也可以看出，在试验过程中，曲线的斜率是保持不变的，表明试样的膨胀速率是保持不变的。

从图4中还可以看出，围压一样的情况下，平面应变试验得到的曲线比常规三轴压缩试验更接近纵轴，表明在相同大主应变的条件下，平面应变试验会引起更大的试样膨胀。常规三轴压缩条件下中主应力是不变的，σ3方向的体积膨胀量主要是由 σ1的作用引起的;平面应变试验中，σ2在剪切过程中是逐渐增加的，σ3方向的膨胀则是由σ1和σ2的共同作用引起的，故相对较大。本文的试验结果与文[15]的分析结果基本一致。

3.4 体积应变与广义剪应变之间的关系

图5绘出了当围压为50 kPa、100 kPa、150 kPa时，含细粒土平面应变试验和常规三轴压缩试验得到的体应变和广义剪应变之间的曲线关系。纵坐标是体应变εv，横坐标是广义剪应变εs，可由式(5)求取。

图5 平面应变试验和常规三轴压缩试验εv～εs之间的关系

从图5可以看出，在试验初始阶段，体积应变会有一个小的增加过程，直至增大到最大值，然后开始减小，对应的试验过程就是试样在开始阶段由于平均应力的增加体积会有一个小的压缩过程，然后开始膨胀。同时可见在相同的试验条件下，平面应变试验中的εs远小于常规三轴试验，其原因在于平面应变试验中中主应力方向的应变为零，且平均应力比常规三轴试验中的要大。

4 结论

通过对含细粒土砂进行平面应变试验和常规三轴试验，可以得出如下结论:

(1)在相同围压下，平面应变试验的偏差应力及广义剪应力大于常规三轴压缩试验，说明平面应变状态下含细粒土砂的强度较高;

(2)在相同的竖向压缩位移，即相同的大主应变下，平面应变试验的广义剪应变最大值远大于常规三轴试验;同时，也可以看出平面应变试验下，小主应变反映的侧向膨胀更大;

(3)在相同的试验条件下，平面应变试验中的体积应变远小于常规三轴试验。

由此说明，应力状态对土的力学特性有重要的影响，应依据工程中其实际的受力状态选择相应的试验方法来确定力学特性。

致谢:感谢大连理工大学工程力学系岩土与环境力学实验室对本实验的大力支持，感谢曾飞涛博士生对本试验的帮助。

[1]Lade P V，Duncan J M. Cubical triaxial tests on cohesionless soil[J]. Journal of Geotechnical and Geoenvironmental Engineering，2014，101(10):793-812.

[2]Alshibli K A，Stein Sture. Shear bands formation in plane strain experiments of sand[J]. Journal of Geotechnical and Geoenvironmental Engineering，2000，126(6):495-503.

[3]Finno R J，Harris W W，Mooney M A，et al. Shear bands in Plane strain compression of loose sand[J].Geoteehnique，1996，47(1):149-165.

[4]Alshibli K A，Batiste S N，Sture S. Strain localization in sand:plane strain versus triaxial compression[J]. Journal of Geotechnical and Geoenvironmental Engineering，2003，129(6):483-494.

[5]Hayano K，Maeshiro T，Tatsuoka F，et al. Shear banding in a sedimentary soft mudstone subjected to plane strain compression[J]. Geotechnical Testing Journal，1999，22(1):67-79.

[6]李广信，张其光，黄勇男.土体平面应变方向上的主应力[J].岩土工程学报，2001，23(3):358-361.

[7]张启辉，李 蓓，赵锡宏，等.上海粘性土剪切带形成的平面应变试验研究[J].大坝观测与土工测试，2000，24(5):40-43.

[8]宋新江，徐海波.平面应变条件下水泥土强度特性试验研究[J].岩土力学，2011，32(8):2325-2330.

[9]邱成春，张孟喜，魏 伟.平面应变条件下网格状带齿加筋砂的强度分析[J].岩土力学，2011，32(增 2):313-318.

[10]陈 鸥，左永振，孔宪勇.砾石土强度和变形的平面应变试验研究[J].人民长江，2010，41(9):69-72.

[11]马险峰，望月秋利，温玉君.基于改良型平面应变仪的砂土特性研究[J].岩石力学与工程学报，2006，25(9):1745-1754.

[12]董建国，李 蓓，袁聚云.上海暗绿色粉质粘土剪切带形成的试验研究[J].工程勘察，2001(3):1-3.

[13]邵龙潭，孙益振，王助贫，等.数字图像测量技术在土工三轴试验中的应用研究[J].岩土力学，2006，27(1):29-34.

[14]程展林，丁红顺，曾 玲.平面应变试验与简化数值分析[J].长江科学院院报，1995，12(3):37-43.

[15]施维成，朱俊高，张坤勇，等.平面应变条件下粗粒土的变形特性试验研究[J].岩土力学，2013，34(1):101-108.