一类函数零点问题的推广
2015-12-21郑华盛
郑华盛
(南昌航空大学数学与信息科学学院,南昌330063)
一类函数零点问题的推广
郑华盛
(南昌航空大学数学与信息科学学院,南昌330063)
[摘要]通过对几道关于函数在满足一类特定的积分等式条件下的零点存在性典型证明题进行观察和深入地分析,提出了一类具有普适性的命题,并给予证明和推广.
[关键词]函数零点; 函数线性无关; 定积分; 等式; 推广
有关函数的零点存在性问题是微积分学中的一类值得探究的问题.文[1-6]中分别给出了几道满足一类特定积分等式条件的函数零点存在性的典型证明题:
(i) 设函数f(x)在[a,b]上连续,且
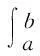
证明至少存在两个不同的点ξ1,ξ2∈(a,b),使
f(ξ1)=f(ξ2)=0,
即f(x)在(a,b)内至少有两个零点.
(ii) 设函数f(x)在[a,b]上连续,且
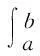
证明f(x)在(a,b)内至少有两个零点.
(iii) 设函数f(x)在[0,π]上连续,且

证明在(0,π)内至少存在两个不同的点ξ1,ξ2,使f(ξ1)=f(ξ2)=0.
(iv) 设函数f(x)在[a,b]上连续,g(x)在[a,b]上有一阶连续导数,且g′(x)≠0,
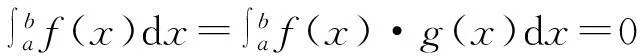
证明至少存在两个不同的点ξ1,ξ2∈(a,b),使f(ξ1)=f(ξ2)=0.
(v) 设函数f(x)在[0,π]上连续,且

证明在(0,π)内至少存在两个不同的点ξ1,ξ2,使f(ξ1)=f(ξ2)=0.
(vi) 设函数f(x)在[a,b]上连续,且

证明f(x)在(a,b)内至少有n+1个零点.
(vii) 设函数f(x)在[a,b]上连续,且

证明f(x)在(a,b)内有无穷多个零点.
那么,能否由上述几个证明题得到一般性的结论?
1预备知识
下面,先给出函数线性无关的定义:
定义1[7]设有定义在区间I上的n个函数fi(x) (i=1,2,…,n),若存在n个不全为零的常数ki(i=1,2,…,n),使得当x∈I时

恒成立,则称n个函数f1(x),f2(x),…,fn(x)在区间I上线性相关;否则称为线性无关.

通过对上述几个实例的观察,注意到它们的被积函数中所含1,x及1,ex在(a,b)上是线性无关的,1,cosx及sinx,cosx在(0,π)上是线性无关的,1,x,x2,…,xn在(a,b)上是线性无关的. 能否以此为主线,归纳出一般性命题? 经过对上述几个实例证明思想的深入分析,得到以下几个一般性命题.
2主要结论
命题1设函数f(x),g1(x)在[a,b]上连续,g1(x)≠0(∀x∈(a,b)),且
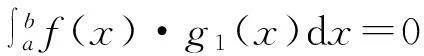
则f(x)在(a,b)内至少有一个零点.
证(反证法)假设f(x)在(a,b)内无零点,则∀x∈(a,b),f(x)恒大于0或恒小于0.又由已知g1(x)≠0(∀x∈(a,b))及g1(x)的连续性,必有g1(x)恒大于0或恒小于0,于是f(x)·g1(x)恒大于0或恒小于0,从而
参加实验的孩子18岁时,Walter Mischel做了跟踪调查,发现那些等待时间长的孩子,学业成功率明显超过等待时间短的孩子:他们的SAT(美国大学入学考试)成绩平均高出210分。其他方面也显示出优势:社交能力更强、事业成功、家庭和谐、体质指数更胜一筹。

这与已知矛盾.故得证.
注1也可以对f(x)·g1(x)用积分中值定理,再由g1(x)≠0(∀x∈(a,b))得证.
命题2设函数f(x),g1(x),ρ(x)在[a,b]上连续,
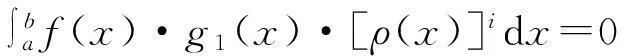
函数1,ρ(x)在(a,b)内线性无关,且ρ(x)在(a,b)内单调,则f(x)在(a,b)内至少有两个零点.
证(反证法)由命题1知f(x)在(a,b)内至少有一个零点,假设f(x)在(a,b)内仅有一个零点x0,则由
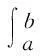
知,f(x)·g1(x)在(a,x0)与(x0,b)内异号.不妨设x∈(a,x0),f(x)·g1(x)>0;x∈(x0,b),f(x)·g1(x)<0. 由已知1,ρ(x)在(a,b)内线性无关,于是ρ(x)在(a,b)内不恒为常数. 又ρ(x)在(a,b)内单调,不妨设ρ(x)单调增加,则当x∈(a,x0)时,ρ(x)≤ρ(x0);当x∈(x0,b)时,ρ(x)≥ρ(x0). 故

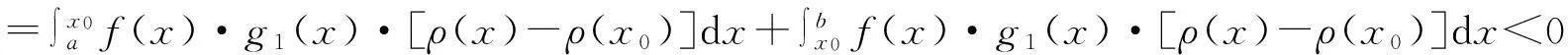
这与已知矛盾.故得证.


命题3设f(x),g1(x),ρ(x)在[a,b]上连续,
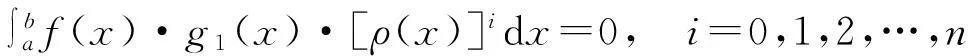
1,ρ(x),ρ2(x),…,ρn(x)在(a,b)内线性无关,且ρ(x)在(a,b)内单调,则f(x)在(a,b)内至少有n+1个零点.
证(用数学归纳法)当n=0时,即为命题1,结论成立;当n=1时,即为命题2,结论成立;
假设n=k时结论成立,则f(x)在(a,b)内至少有k+1个零点,下面用反证法证明:当n=k+1时结论也成立,即证f(x)在(a,b)内至少有k+2个零点.
假设函数f(x)在(a,b)内恰有k+1个零点,不妨设零点分别为x1,x2,…,xk+1,其中a
取
G(x)=f(x)·g1(x)·(ρ(x)-ρ(x1))·(ρ(x)-ρ(x2))…(ρ(x)-ρ(xk+1)),
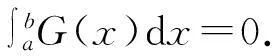
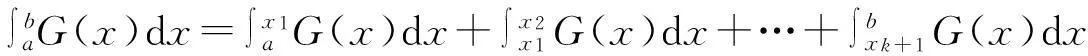
由已知∀x∈(a,b),g1(x)≠0及g1(x)的连续性,于是g1(x)在(a,b)上不变号,不妨设g1(x)>0(∀x∈(a,b)). 又由已知ρ(x)在(a,b)内单调,不妨设ρ(x)单调增加,于是
(ρ(x)-ρ(x1))·(ρ(x)-ρ(x2))…(ρ(x)-ρ(xk+1))
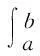
综上所述,由数学归纳法即可证得.
特别地,取g1(x)=1,ρ(x)=x,则由命题3可得前述典型证明题(vi). 类似地,可利用命题3设计和构造函数的零点存在性证明题. 如,取g1(x)=1,ρ(x)=ex,即得
推论1设f(x)在[a,b]上连续,
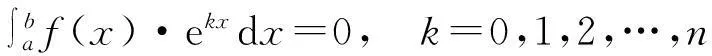
则f(x)在(a,b)内至少有n+1个零点.
类似于命题3,可证得
命题4设函数f(x),g1(x)在[a,b]上连续,

1,ρ(x),ρ2(x),…在(a,b)内线性无关,且ρ(x)在(a,b)内单调,则f(x)在(a,b)内有无穷多个零点.
特别地,取g1(x)=1,ρ(x)=x,即得前述证明题(vii).
3结束语
本文通过对一类满足特定积分等式条件下的函数的零点存在性典型证明题及其证明方法进行深入地观察和细致地分析,归纳出具有普适性的一般性命题,并作进一步推广. 这种由特殊至一般,对已有命题做合乎逻辑的分析,进而提出一般性命题,并加以证明和推广的过程是研究性与创新性学习的基本形式之一. 对从事数学教学的教师也有一定的参考价值,由此可以编制出一些在满足特定积分等式条件下的函数至少有两个及更多零点的存在性新证明题.
[参考文献]
[1]裴礼文.数学分析中的典型问题与方法[M].2版.北京:高等教育出版社,2006:362.
[2]陈仲.高等数学竞赛题解析[M].南京:东南大学出版社,2008:80,84-85.
[3]林源渠,方企勤. 数学分析解题指南[M].北京:北京大学出版社,2003:173-174,186.
[4]徐斌.高等数学证明题500例解析[M].北京:高等教育出版社,2007:39-40,308-314.
[5]谢惠民,恽自求,易法槐,钱定边.数学分析习题课讲义(上册)[M].北京:高等教育出版社,2003:316-317.
[6]钱昌本. 解题之道-高等数学范例剖析240题[M].西安:西安交通大学出版社,2004:104-106.
[7]同济大学应用数学系. 高等数学(下册)[M].5版.北京:高等教育出版社,2002:296.
[8]阮炯.差分方程和常微分方程[M].上海:复旦大学出版社,2002:46-47.
TheExtensionofaKindofProblemswithZerosoftheFunction
ZHENG Hua-sheng
(SchoolofMathematicsandInformationScience,NanchangHangkongUniversity,Nanchang330063,China)
Abstract:Akindofgeneralitypropositionsispresentedbyobservingandanalyzingseveraltypicalproofproblemsofzerosexistenceofthefunctionwithspecificdefiniteintegralequalities.Andthen,theproofandextensionareimplemented.
Keywords:zeroofafunction;linearindependenceoffunctions;definiteintegral;equality;extension
[基金项目]中央高校业务费资助项目(河海大学);河海大学小型教改项目(2014);南京农业大学工学院研究型教改项目(2014);河海大学文天学院大学数学课程教学团队(20002),安徽省级项目,《高等数学》教学改革研究(zl201206),重点教学研究项目(校内)
[收稿日期]2015-03-29
[中图分类号]O172.2;O13
[文献标识码]C
[文章编号]1672-1454(2015)04-0045-04
[基金项目]江西省及南昌航空大学教学改革研究项目(JXJG-13-8-18,JY1329);江西省自然科学基金项目(20114BAB201001);江西省教育厅科技项目(GJJ12431)
[收稿日期]2014-12-26; 2015-04-22
