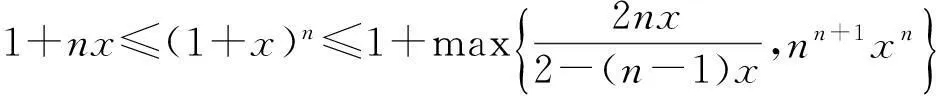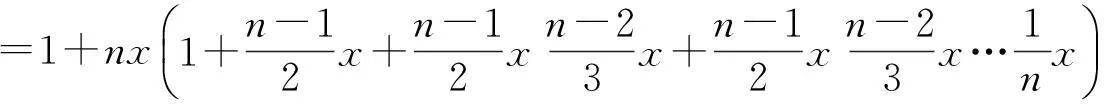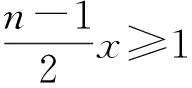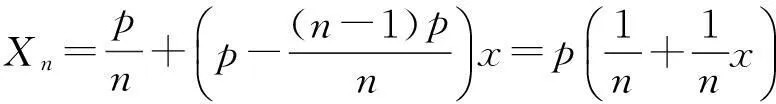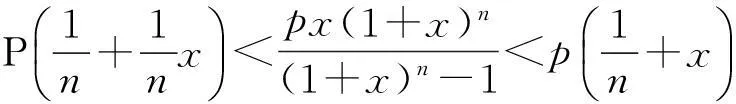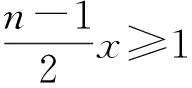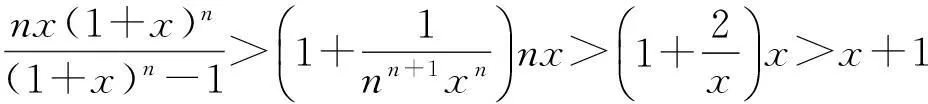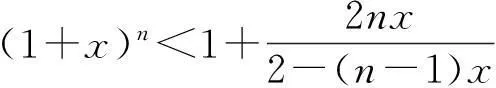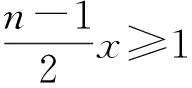Bernouli不等式的改进与应用
2015-12-21戴志敏冯孝周
戴志敏, 冯孝周
(西安工业大学理学院, 西安710032)
Bernouli不等式的改进与应用
戴志敏,冯孝周
(西安工业大学理学院, 西安710032)
[摘要]对一般的Bernouli不等式满足的条件作了一个新的限定,利用二项式定理和等比数列的性质并采用分类讨论的思想证明了一个新的Bernouli不等式,由此不等式证明了经济学中的等额本金还款法和等额本息还款法的差异,并利用数值计算实验验证了此差异,从而由此结论给出了针对不同人群的还贷策略.
[关键词]Bernouli不等式; 二项式定理; 等比数列; 等额本金还款法; 等额本息还款法
1引言
Bernouli不等式是数学中的一个重要不等式,在证明一些重要的不等式,如Young不等式,Hölder不等式、几何算术平均不等式等方面发挥着重要的作用[1]. 除此之外,Bernouli不等式在研究函数的单调性、极限、连续以及级数的收敛性等方面都有着广泛的应用[2].Bernouli不等式的一般形式[3],即下面的引理1.
引理1设x>-1,α<0或者α>1,则有
(1+x)α≥1+αx.
(1)
假若0<α<1,则有
(1+x)α≤1+αx.
(2)
(1) ,(2) 两式成立的充要条件为x=0.
特别地,当α=n∈且n≥1,则成立
1+nx≤(1+x)n.
(3)
进一步假定x>0,由函数ex>1+x, 有
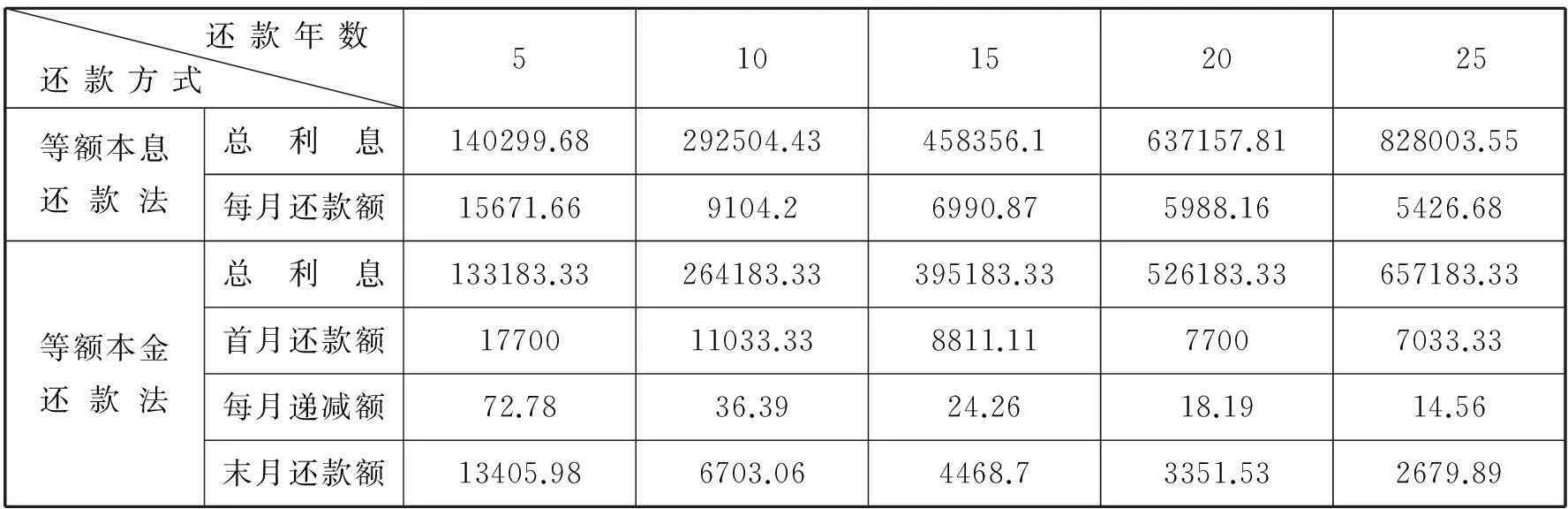
1+nx≤(1+x)n (4) 更多有关Bernouli不等式的介绍见文献[3-4]. 以上谈到了Bernouli不等式在数学上的应用,本篇文章将研究Bernouli不等式如何应用到经济学中两种常见的还款方式,即等额本金还款法和等额本息还款法差异的比较上. 2新的Bernouli不等式及证明 Bernouli不等式(3)和(4)用来比较等额本金还款法和等额本息还款法的差异是不够的,为此需给变量x限定一个新的范围0 定理1设n为大于等于1的正整数,且x满足0 (5) 此不等式的两边取等号当且仅当n=1时成立. 证不等式的左边不需要证明,只需要证明不等式的右边. 当n=1时,显然成立. 当n>1时,对(1+x)n利用二项式展开定理, 因此 从而有式(5)成立. 3新的Bernouli不等式的应用 近年来, 购买商品房已成为我国城镇居民消费的一个重要部分.面对高昂的房价, 绝大多数购房者选择了向银行贷款.在向银行贷款时,必须考虑两个因素: 一是还款能力;二是利息支出.目前银行贷款就还款方式而言,主要有等额本金还款法与等额本息还款法.针对不同的还款办法,文献[5]运用数学软件Mathematica给出月还款额与利息总额对照表, 并通过对比,比较出这种还款方式的差异.而文献[6]则用数学的方法证明了这种差异.本文将用新的Bernouli不等式来从另一种思路来证明这种差异. 为此,先来对等额本金还款法与按等额本息还款法作一个简单的介绍. 假设某人欲向银行贷款p元,计划分n期还清贷款,在银行每期利率保持为x不变的情况下,他有两种选择还贷方式. 如果按等额本金还款法,用Xi表示每期还款数,他每期应还款额有下面的计算公式[7-8], ⋮ (6) 可以看出按等额本金还款法每期还款数构成了一个递减的等差数列,并且如果利率上调,则每期还款额相应增加,利率下调则相反. 如果用X表示到第n期末还款总额,则有 (7) 如果按等额本息还款法,用Yi表示每期还款数,他每期应还款额有下面的计算公式[7-8] (8) 可以看出等额本息还款法每期还款额是一个固定数字.计算 可知利率上调时,等额本息还款法每期还款额相应增加,利率下调则相反. 如果用Y表示到第n期末还款总额,则有 (9) 为了比较等额本金还款法与等额本息还款法的差异,先来证明下面一个定理. 定理2假设n与x分别满足条件n>1和0 (10) (11) 证不等式(10)的证明:首先证左边. 时,则由Bernouli不等式(1)有 (1+x)1-n>1+(1-n)x((1-n)<0, 0 ⟺(1+x)n-1[1+(1-n)x]<1⟺(1+x)n-1 再证右边.由Bernouli不等式(1) 1+nx<(1+x)n(n>1) 故不等式(10)得证. 不等式(11)的证明: 故不等式(11)得证. 4数值实验与结果分析 由定理2的结论不难得出这样的事实: 在保持银行基准利率不变的条件下,等额本金还款法虽然首期还款比等额本息还款法高,但每期逐渐递减,且末期还款与到期还款总额都比后者要少. 下面以买一套商品房贷款80万元,分别以等额本息还款法与等额本金还款法,以5年为间隔计算25年内计算这两种还贷方法的总利息与每月还款额,假设银行当前基准利率为6.55%,则月利率为6.55%/12=5.46‰,结果列成下表. 表 1 单位:元 从表1来看,数值计算结果完全验证了新的Bernouli不等式在本篇论文中证明的结果. 尽管利用Bernouli不等式证明了并用数值计算验证了等额本金还款法与等额本息还款法的差异,但是实际选择何种还款方式应综合多种因素做出适合自己的合理选择.由于贷款者选用等额本金还款法还款初期压力比较大, 而等额本息还款法则在整个还款期限内还款压力相对较低.对高收入人群且对贷款利息比较敏感的购房者、自己极有可能提前还款的购房者以及个人认为住房贷款利率中途极有可能上调的购房者,最好选用等额本金还款法.对经济收入相对紧张的人群、以及个人认为住房贷款利率中途极有可能下调的购房者,选择等额本息贷款法可以减轻其还贷压力,从而保证自己的生活不受影响[9]. [参考文献] [1]邢家省,王洪志.从贝努利不等式到Hölder不等式演变过程及应用[J].吉首大学学报(自然科学版),2010,31(2):10-14. [2]张学茂. Bernouli不等式的证明及应用[J].阜阳师范学院学报(自然科学版),2010,27(3):30-32. [3]匡继昌.常用不等式[M].济南:山东科学技术出版社,2004:127-128. [4]乔希民.一个新的积分不等式的推广及应用[J].延安大学学报(自然科学版),2005,24(2):21-29. [5]张学山,李路,江开忠.购房贷款方案的优化问题[J].上海工程技术大学学报,2005,19(2):166-171. [6]李宝凤.数学在借贷中的应用[J].唐山师范学院学报,2011,33(2):48-49. [7]赵玉梅.个人住房按揭还贷方式探析[J].广西民族大学学报(哲学社会科学版),2008:51-56. [8]高大成.浅谈数学在生活中的应用[J].学术研究,2013(8):202-203. [9]郭蔚.等额本息还款法与等额本金还款法哪种更好[J].辽宁行政学院学报,2005,7(3):69-70. Improvement of Bernouli Inequality and Its and Applications DAIZhi-min,FENGXiao-zhou (School of Science, Xi’an Technological University, Xi’an 710032, China) Abstract:The general conditions of Bernouli inequality to meet is imposed on a new limit, using the binomial theorem and the properties of the geometric sequence and the idea of using the classification discussing prove a new Bernouli inequality, with which it is proved that the differences of equal principal repayment method and equal installments of principal and interest repayment method in economics; and these differences are verified with numerical experiments, thus the loan policies for different populations are given. Key words:Bernouli inequality; binomial theorem; geometric sequence; equal principal repayment method; equal installments of principal and interest repayment method [中图分类号]O29;F830.5 [文献标识码]B [文章编号]1672-1454(2015)04-0020-05