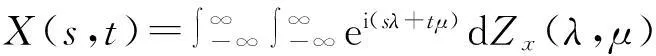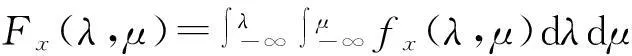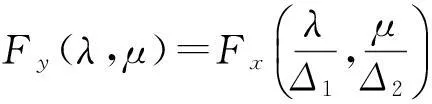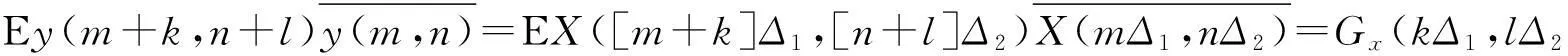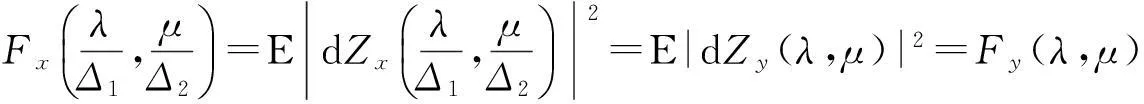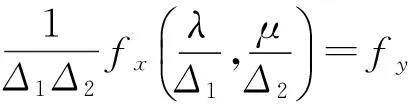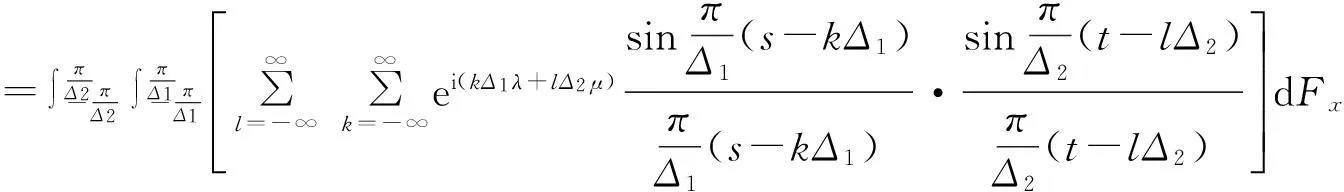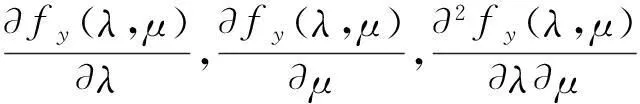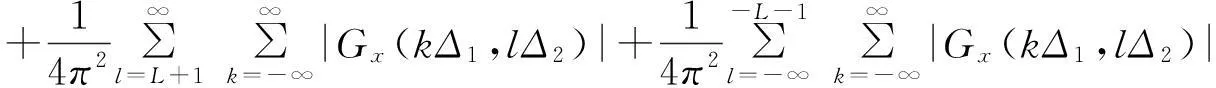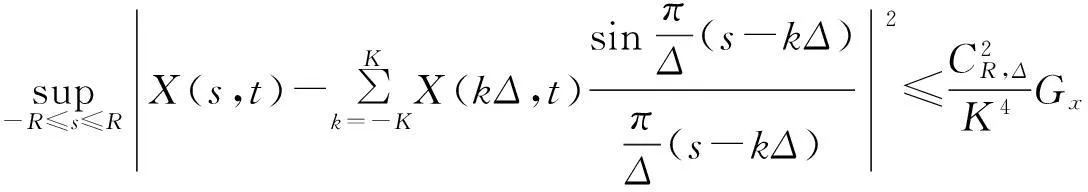具有连续参数的宽平稳随机场的采样定理及应用
2015-12-21徐业基
徐业基
(复旦大学管理学院统计学系,上海200433)
具有连续参数的宽平稳随机场的采样定理及应用
徐业基
(复旦大学管理学院统计学系,上海200433)
[摘要]研究具有连续参数的宽平稳随机场的采样定理,并求出它的相关函数;谱密度函数和谱函数的估计式以及它们的一致收敛的速度.
[关键词]宽平稳随机场; 相关函数; 谱密度函数; 谱函数; 采样定理
为方便,本文只讨论具有两元连续参数的宽平稳随机场,其方法和所得结果可以推广到n元的情况.
设{X(s,t),-∞ 其中Zx(λ,μ)是正交增量的两元随机函数,且对平面上任意两个Borel可测集s1及s2,成立着 称Zx(λ,μ)与Fx(λ,μ)各为{X(s,t)}的随机谱函数与谱函数.若 则fx(λ,μ)称为谱密度.记{X(s,t)}的相关函数为Gx(s,t).则 y(k,l)=X(kΔ1,lΔ2),(k,l=0,±1,±2,…), 则{y(k,l)}是均值为零的离散宽平稳随机场,它的相关函数为Gx(kΔ1,lΔ2). 谱函数为 谱密度为 证由于 Ey(k,l)=EX(kΔ1,lΔ2)=0, 故{y(k,l)}是离散宽平稳随机场,有唯一表示式 故 引理3[1]积分的估计如下: 定理1设{X(s,t),-∞ 且上述级数对(s,t)在任意有限区域:|s|≤R,|t|≤T内是均方一致收敛的,且 (1) 应用不等式: |akbl-ab|2=|(ak-a)(bl-b)+b(ak-a)+a(bl-b)|2 ≤3|ak-a|2|bl-b|2+3|b|2|ak-a|2+3|a||bl-b|2. 再由引理3即得定理1的证明. 下面讨论定理1的应用 定理2设{X(x,t)}是实的宽平稳随机场,满足定理1的条件,则它的相关函数Gx(s,t)有下列估计式: 这里 , E(kΔ1,lΔ2)=Gx(kΔ1,lΔ2). 证由定理1及Gx(kΔ1,lΔ2)的谱分解得 下面用定理1的证法和引理3,即可证明定理2. 定理3设{X(s,t)}是实的宽平稳随机场,满足定理1的条件,记 y(k,l)=X(kΔ1,lΔ2),(k,l=0,±1,±2,…), (2) 其中 若进一步设 存在且有界,则 (3) 证由引理1和引理2得Gy(k,l)=Gx(kΔ1,lΔ2)及 即得(2).若进一步设 存在且有界,利用Gy(k,l)的谱分解 对积分进行p+q次分部积分(可参看[2])即得(3)式. 定理4设{X(s,t)}是实的宽平稳随机场,满足定理3的条件,Fy(λ,μ)是y(k,l)=x(kΔ1,lΔ2)(k,l=0,±1,±2,…)的谱函数,则 (4) 这里 若进一步设 存在且可积,则 (5) 证利用 即得(4)的证明.关于(5)式的证明法和定理3一样,故从略. 定理5设{x(s,t),-∞ (Δ是正的常数),即Fx(λ,μ)的谱测度集中在带状区域中),则 证参看[1],并用引理3得 注我们也可以在满足定理5的条件下来讨论具有连续参数宽平稳随机场的相关函数、谱密度和谱函数的估计. [参考文献] [1]徐业基.关于平稳随机过程的采样定理的一致收敛速度[J].大学数学,2009,25(6):48-51. [2]徐业基.关于平稳承受机过程的采样定理的一致收敛速度(Ⅱ)[J].大学数学,2014,30(3):10-14. [3]惠军.平稳过程采样定理的一个注记[J].合肥工业大学(自然科学版),2000,23(6):969-975. [4]复旦大学.概率论(随机过程)[M].3版.北京:人民教育出版社,1981. [5]Hobson E W. The theory of functions of a real variable and theory of fourier’s series (VOLUME Ⅱ)[M]. New york:Dover Publications. NC, 1926. The Discrete Samples Theorems of the Weak Stationary Stochastic Fields with Continuous Parameter and its Applications XUYe-ji (Fudan University, Shanghai 200433, China) Abstract:The discrete samples theorems of the weak stationary stochastic fields with continuous parameter are discussed. The estimate of the correlation of function and density function of spectrum and spectrum function also are discussed. Key words:weak stationary stochastic fields; correlation of function; density function of spectrum; spectrum function; discrete sample [基金项目]陕西省自然科学基金项目(2013JC2-31); 西安工业大学校长基金(XAGDXJJ1323) [收稿日期]2014-11-03;[修改日期]2015-07-13 [中图分类号]O211.61 [文献标识码]A [文章编号]1672-1454(2015)04-0014-06