正交异性钢桥面横向焊接接头的疲劳寿命估算

陈世鸣，陆云，周聪，顾萍



正交异性钢桥面横向焊接接头的疲劳寿命估算

陈世鸣1，陆云1，周聪2，顾萍1

(1. 同济大学土木工程学院，上海，200092；2. 坎特伯雷大学机械工程系，新西兰基督城，8140)

针对正交异性铁路钢桥面构造细节，设计2个足尺钢桥面构件进行静载和高周疲劳承载试验。在试验研究的基础上，建立钢桥面有限元模型，并进行分析计算，计算结果与试验值基本吻合。在1阶段模型的基础上，采用子模型技术建立纵肋焊缝位置带半椭圆表面裂纹的2阶段模型，用退化奇异单元模拟该部位裂纹尖端应力场，通过位移外推得到不同裂纹深度下裂纹尖端的应力强度因子。基于初始裂纹尺寸的合理判定，对Paris公式积分推导得到纵肋焊接接头裂纹扩展曲线并估算疲劳寿命，计算结果解释了试验中裂纹的萌生和发展规律。建议钢桥面纵肋焊接接头按EC33中的71级或铁路桥梁钢结构设计规范中IX细节进行疲劳设计。

正交异性钢桥面；疲劳试验；疲劳寿命；应力强度因子；子模型技术

正交异性钢桥面现场横向连接采用钢桥面与纵肋焊接连接，是桥面施工时常用的连接方式。然而，大量钢桥面疲劳事例表明钢桥面横向焊接接头对疲劳敏感。早在20世纪70年代，欧洲煤钢联盟(ECSC)进行了带闭口肋钢桥面的疲劳研究，ECSC的研究报告[1−2]指出：桥面板应采用双坡口对接焊或者使用陶瓷衬垫的单坡口焊接，不允许采用永久性的钢衬垫(此项成果后被欧洲规范Eurcode3[3]采纳)。Kolstein等[4]通过足尺钢桥面板构件的疲劳试验，研究了正交异性钢桥面纵肋连接嵌补段的疲劳性能，指出了纵肋单坡口焊接疲劳强度与肋壁和桥面板之间焊缝的宽度和焊接的质量有关。Xiao等[5]对日本Kinuura桥进行了检测，发现大量疲劳裂纹出现在纵肋对接接头。我国在钢桥面施工时常用焊接连接，但我国桥梁钢结构设计规范对于钢桥面横向焊接接头的疲劳性能并没有专门的规定。唐亮等[6−8]对钢桥面横向焊接接头的受力特性和疲劳强度也进行了相应的研究，对疲劳寿命的估算主要基于−曲线的传统评估方法。断裂力学疲劳评估方法在航空、海洋等领域得到许多应用，但在钢桥疲劳寿命评估中还很少采用。本文作者结合某铁路桥的钢桥面，对钢桥面横向焊接接头进行静力、疲劳试验研究，同时采用有限元子模型技术建立带裂纹体的精细子模型，基于断裂力学理论进行钢桥面横向焊接接头疲劳寿命估算[9−10]。

1 试件及试验布置

设计、制作2个足尺钢桥面试件(LH1和LH2)，2个试件的形状和尺寸相同，均由2个纵肋(U形肋)、2根横梁和钢桥面板组成，如图1所示。桥面板长×宽为2.0 m×1.2 m，厚16 mm，纵肋板厚8 mm，横梁腹板、翼板厚分别为14 mm和16 mm，纵肋尺寸和间距、构造细节、制作工艺、材料均与实桥钢桥面相同。试件材质为Q345qD钢材，其化学成分及力学特性检测结果符合GB/T 714—2008“桥梁用结构钢”[11]。制作时先完成桥面板的对接焊缝，再将纵肋嵌补段塞入空隙，将其与两侧的纵肋焊接，最后完成纵肋嵌补段与桥面板焊接。嵌补段U肋采用单边V型坡口，背面贴钢衬垫，坡口加工在嵌补段上。桥面盖板对接采用不带钝边的V型坡口焊，背面贴陶瓷衬垫，单面焊双面成型。试件所有焊缝按照TB 10212—2009“铁路钢桥制造规范”[12]进行检测，均符合Ⅰ级要求。

试验加载由液压脉动试验机通过分配梁进行4点加载。试件为横梁两端简支支承，通过横梁下翼缘4个滚轴支座来施加约束(见图1)。

单位：mm

(a) 钢桥面平面及侧面；(b) 钢桥面立面及剖面

图1 试件及应变片布置图

Fig. 1 Arrangement plans of specimens and strain gages

试件加载大小根据列车轴重和试验机加载能力确认，为了模拟轮载并使加载面受力均匀，每个加载点垫宽×长为140 mm×320 mm的钢板(见图1(a)中阴影部位)。试验包括静载试验和疲劳试验：静载试验荷载分级加载至400 kN再卸载至0 kN；由于纵肋焊缝对接处残余应力复杂，容易存在初始缺陷诱发裂纹，在试件纵肋对接焊缝附近布置应变片(见图1)。LH1疲劳加载分为3个阶段，第1阶段min=100 kN，max= 190 kN，疲劳加载至1.00×106次；第2阶段min=100 kN，max=235 kN，疲劳加载至2.50×106次；第3阶段min=100 kN，max=275 kN。LH2疲劳试验荷载min=100 kN，max=240 kN，2试件加载频率均为4 Hz。

2 静载试验

疲劳试验前、中、后分别进行静力加载试验。根据静载数据来判别试件受力特性变化以及疲劳裂纹对其受力性能的影响。

表1所示为试件LH2在疲劳试验前在400 kN荷载的静载试验实测结果及有限元计算结果，计算方法为有限元计算分析，表1中dy1和dy2是跨中的位移测点，其余4个为应力测点，布测位置见图1。

从表1可知：试件的位移实测值与计算值基本吻合。纵肋焊接连接附近的测点由于焊缝的存在使得测点实测值与理论值略有偏差。总体而言，试件实测受力特性与理论分析基本一致。

表1 测点实测结果与计算结果

3 疲劳试验

试件LH1和LH2的疲劳裂纹主要都是先从纵肋焊缝1外侧圆弧过渡区出现，然后向纵肋底部和腹板上扩展，如图2和3所示。从图2可见：LH1疲劳加载至第3阶段时，在焊缝1处圆弧过渡区观察到长 16 cm裂纹。从图3可见：LH2当疲劳加载到1.89×106次时，在焊缝1纵肋外侧圆弧过渡段观察到疲劳裂纹，长度约为40 mm。之后，裂纹较快向纵肋底部和腹板上扩展，加载到2.00×106次，试验结束。

图4所示为LH2 的3个测点(sd1，sd2和sd6)的应力幅荷载循环曲线。从图4可见：纵肋外侧发现疲劳开裂时，紧邻的底板中心测点sd2和sd6以及纵肋腹板测点sd1的应力幅明显上升，当裂纹扩展超过上述测点，上述3个测点的应力幅也开始下降。

图2 LH1纵肋裂纹

图3 LH2纵肋裂纹

4 疲劳性能分析

从LH1和LH2的疲劳试验发现：2个试件的疲劳裂纹都出现在纵肋焊缝1外侧圆弧倒角位置，裂纹出现后试件的整体受力特性发生明显变化，裂纹扩展的速度也很快。由于钢结构裂纹初期肉眼难以观察到，一般能够清楚观察到裂纹时，已经进入扩展后期，甚至穿透厚度。取观测到裂纹时的加载次数为试件的疲劳寿命()，未开裂测点取试验总加载次数，裂纹附近测点平均应力幅为名义应力幅()。数据分析中，采用Miner[13]线性准则和疲劳强度公式将LH1不同荷载幅对应的疲劳循环次数转换为最后阶段荷载幅对应的循环次数。

测点：1—sd1; 2—sd6; 3—sd2

美国公路和运输协会标准(AASHTO LRFD)[14]和欧洲钢结构规范(EC3)[15]关于钢桥面纵肋焊接接头的疲劳强度其细节分级分别为D类和71级。其中：AASHTO中D类细节2.00×106次时疲劳强度为 71.2 MPa，故AASHTO疲劳强度曲线与EC3的71级的疲劳强度曲线近于重合。对测点数据采用最小二乘法推算得与的回归曲线，进而得到95%置信度的下限值，如图5所示。

从图5可见：实测数据95%置信度的下限略高于AASHTO-D，EC3-71和铁路桥梁钢结构规范-IX的疲劳强度曲线。结果表明：2个试件钢桥面纵肋焊接接头的疲劳强度都能达到上述规范规定的疲劳强度等级。由此建议纵肋焊接接头的疲劳强度可取为EC3中的71级，或按我国铁路桥梁钢结构设计规范的IX类，2.00×106次时的疲劳强度取为71.9 MPa。

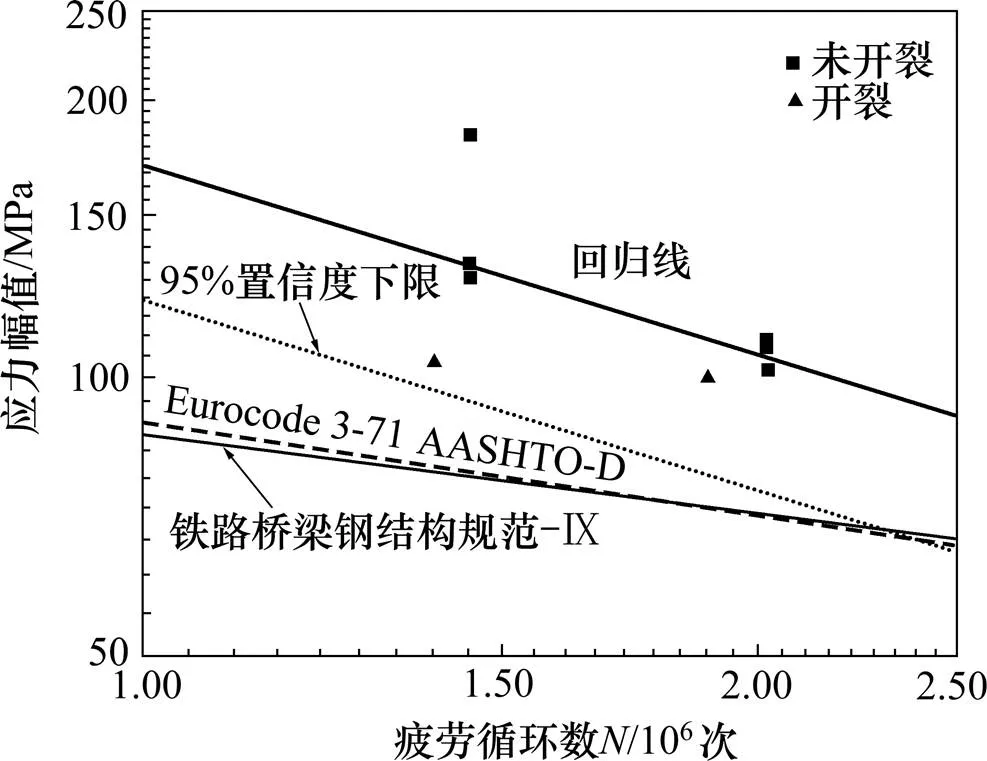
图5 LH1和LH2试验数据与相应S−N曲线对比结果

5 有限元计算分析

对2个试件均建立足尺模型和子模型，进行力学分析和疲劳寿命评估，由于分析的方法和过程具有共性，现以试件LH2为代表来予以说明。

钢桥面有限元计算模型如图6所示，其尺寸、边界条件及加载方式与试验相同，钢桥面建模全部采用solid45单元。考虑到加载过程动力冲击系数的影响，计算中采取应力幅等效的原则来确定计算荷载，即使试件焊缝1的纵向计算拉应力与疲劳试验的实测应力幅值相等，经试算焊缝1处外侧圆弧转角处的应力幅值为115 MPa是整个纵肋截面应力幅值的最大值，与疲劳试验测点sd2实测的应力幅值(见图4)基本一致。图7所示为纵肋焊缝连接处应力云图。

疲劳寿命预测中最关键的是计算裂纹尖端的应力强度因子。本文中纵肋圆弧转角部位并非1块平板，无法通过规范或者手册查阅得到相应的应力强度因子和修正系数。本文采用带裂纹体的子模型分析方法，进行裂纹尖端应力强度因子计算。为了使裂纹处单元划分更细，同时计算速度又不受影响，针对纵肋连接焊缝，采用有限元分析软件ANSYS中20节点的solid95退化奇异单元，建立精细子模型来模拟三维裂纹尖端应力场。子模型采用与整体模型一致的节点位移为输入边界条件，子模型的裂纹尖端指定为奇异点，裂纹尖端网格划分如图8所示。

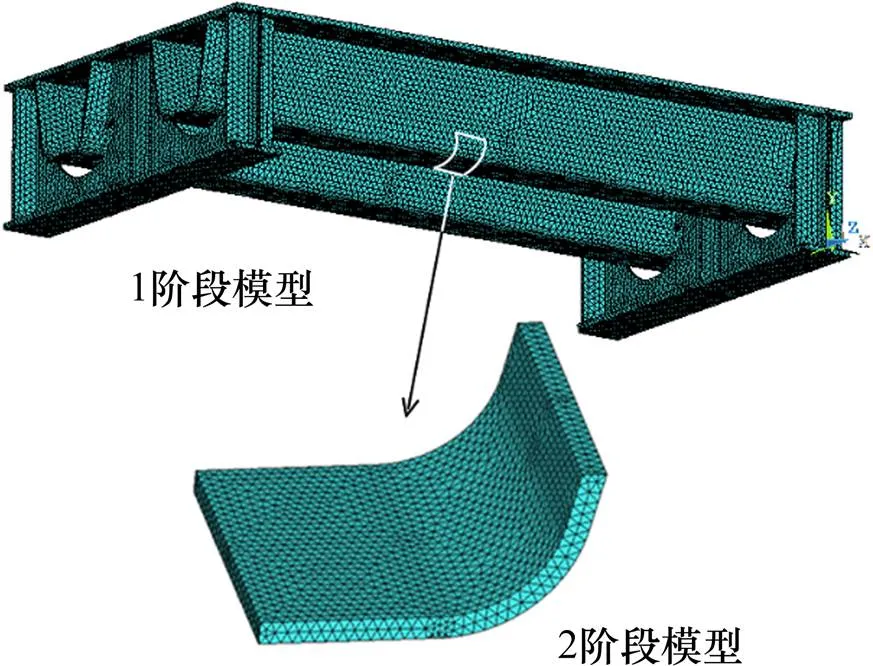
图6 试件有限元计算模型

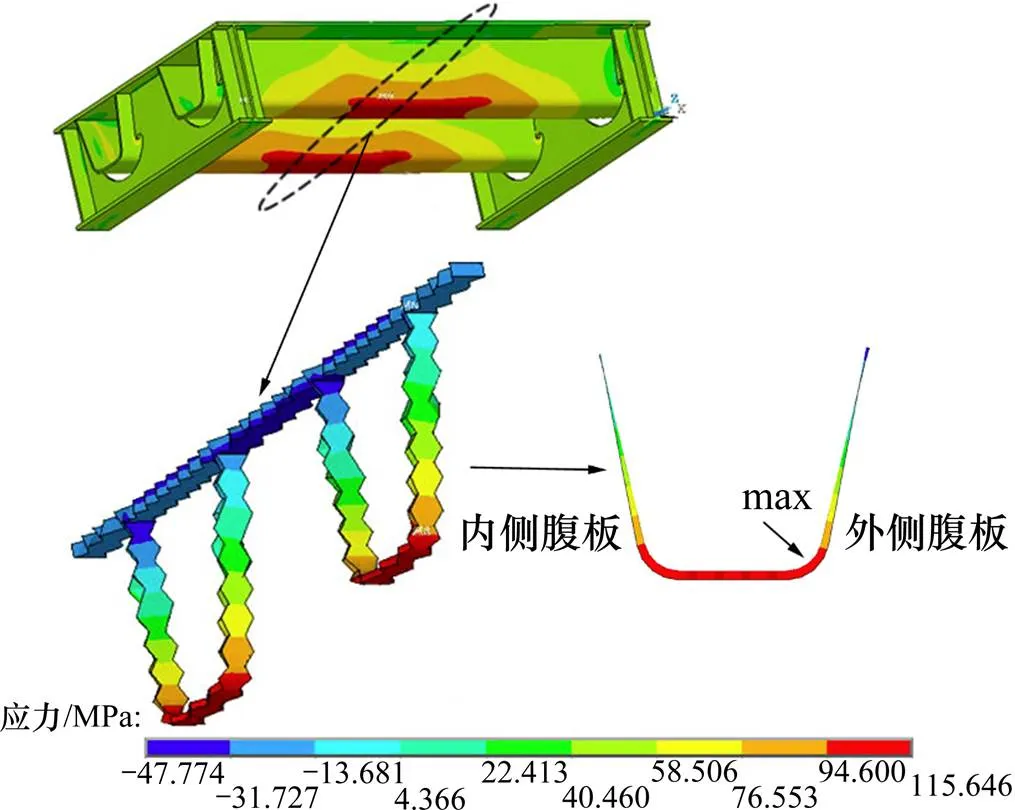
图7 纵肋焊缝连接处应力云图

图8 裂纹尖端处网格划分

采用的计算假定为：1) 纵肋焊缝的裂纹形状为表面半椭圆裂纹，裂纹深度为，长度为2(见图8)；2) 裂纹深度沿纵肋壁厚方向扩展，裂纹前沿主要考虑裂纹最深点的应力强度因子max；3) 裂纹类型为Ι型裂纹。因为纵肋焊缝的裂纹主要受纵向拉应力影响，其他2种裂纹模式的应力强度因子很小。

本文假定/(2)始终为0.2。其原因有2个：1) 文献表明[5, 16]，不同的裂纹深度与裂纹长度比(/2)不会引起很大的应力强度因子变化；2) LH2焊缝处发现裂纹时，裂缝长度(2)为40 mm，贯透纵肋板厚(=8 mm)。故当对LH2进行疲劳寿命估算时，取/(2)=0.2。

依次建立带不同裂纹深度的子模型，对裂纹尖端单元按照ANSYS程序中要求进行网格划分。采用CBDOF命令将整体模型中与子模型边界对应的计算结果作为边界自动赋予到子模型的对应边界位置，并在验证子模型的合理性前提下，使用“位移外推 法”[17]求得与每个裂纹深度对应的，绘制应力强度因子和裂纹深度的关系曲线如图9所示。从图9可见：随的增大而增大，其增长速率在纵肋厚度的中部达到峰值，随后值增长速率渐缓。

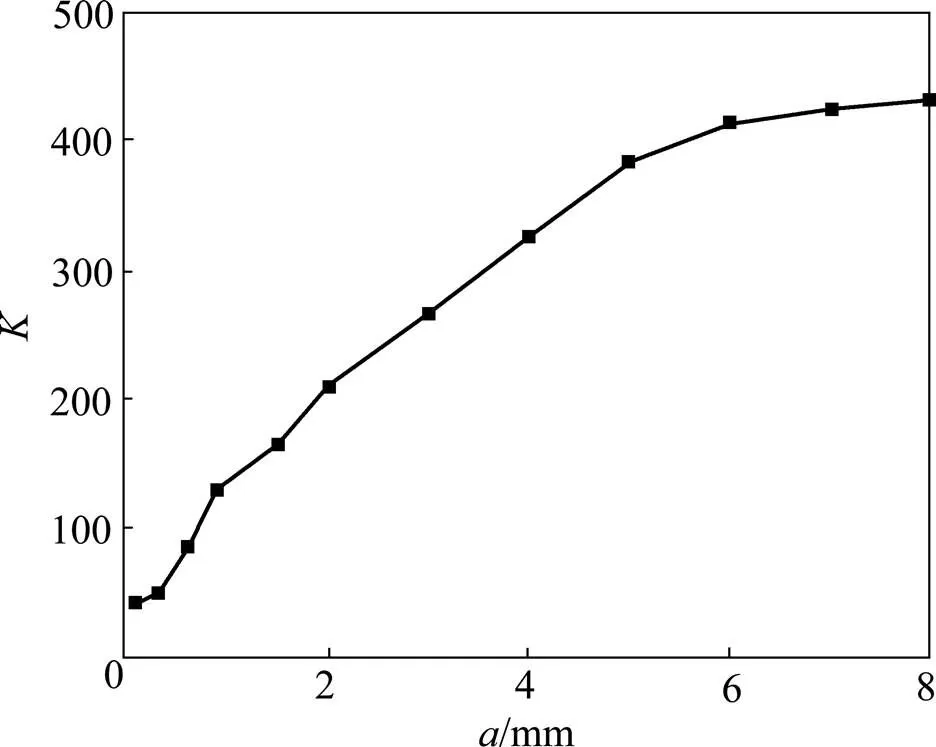
图9 a/(2c)=0.2时的应力强度因子

6 裂纹扩展模拟与疲劳寿命估算

疲劳断裂力学理论[18]认为：疲劳开裂本质上是1个裂纹(疲劳源)的扩展过程。循环应力作用下，裂纹尖端应力集中，裂纹尖端区域形成双向或三向同号应力场，使裂纹扩展直至构件断裂。根据Paris公式，疲劳寿命可表达为

式中：和是与材料有关的常数，可通过试验拟合得到；为疲劳寿命；为裂纹尺寸，i和f分别为裂纹的初始和临界尺寸。

由于受检测手段所限，疲劳裂纹的萌生和早期扩展的试验结果较少，Harris[19]认为：可以用探伤设备的精度下限和疲劳试验结果倒推得到初始裂纹尺寸。Righiniotis等[20]指出：桥梁焊接细节的初始裂纹尺寸平均值的合理下限为0.1 mm。Nguyen等[21]在正交异性钢桥面疲劳试验中，利用试验数据倒推得到钢桥面构造细节处初始裂纹尺寸为0.1 mm。

裂纹尖端应力强度因子的通式[18]为

将根据子模型计算的max和所对应的f代入式(2)，可以得到=0.75(=115 MPa)。假定为常数即0.75，将式(2)代入式(1)，可得：

ai/mm: 1—0.01; 2—0.10; 3—1.00

采用最小二乘法将图9中应力强度因子拟合成的函数，之后代入式(1)中逐步数值积分可得到疲劳寿命与裂纹尺寸的关系曲线(裂纹扩展曲线)，如图11所示。数值积分过程中选取初始裂纹尺寸i=0.10，0.15，0.20，0.25和0.30 mm。从图11可见：不同初始裂纹尺寸所得到的裂纹扩张曲线形状和走势类似。随着初始裂纹尺寸的增大，疲劳寿命相应降低，降低的幅度也依次减小，分别为0.21×106，0.18×106，0.16×106和0.13×106次。表明初始裂纹尺寸对疲劳寿命有较大影响，但随着初始裂纹尺寸增大，其影响作用递减。

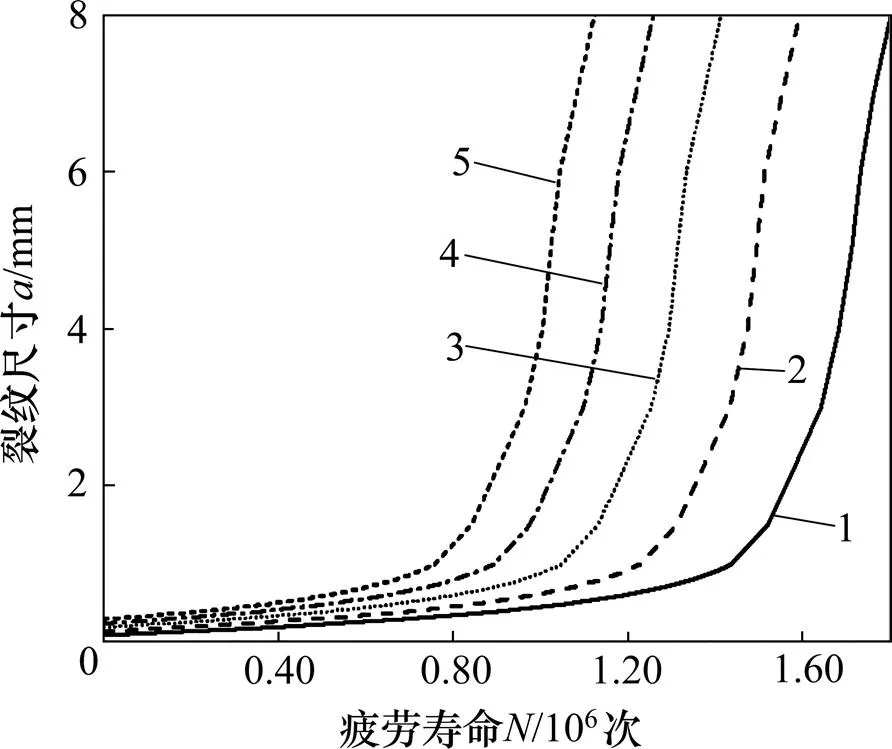
初始裂纹尺寸/mm: 1—0.10; 2—0.15; 3—0.20; 4—0.25; 5—0.30

与试件LH2疲劳加载循环1.89×106次观察到裂纹试验结果相比，初始裂纹尺寸为0.10 mm的积分结果=1.8×106最接近。这也从另外一方面证明假定初始裂纹尺寸为0.10 mm是较合理的。

7 结论

1) 正交异性钢桥面纵肋焊接接头部位为疲劳裂纹易发处，本次试验的2个钢桥面构件均在纵肋焊缝圆弧处出现疲劳裂纹。

2) 建议采用EC3中的71级或我国铁路桥梁钢结构设计规范IX细节的疲劳强度曲线。

3) 钢桥面纵肋纵向应力最大值发生在外侧腹板圆弧转角处；可用退化奇异单元模拟该部位裂纹尖端应力场，通过位移外推求得裂纹尖端应力强度因子与裂纹尺寸关系曲线。

4) 初始裂纹尺寸对疲劳寿命有较大影响，但随着初始疲劳尺寸的增大，该影响作用递减。初始裂纹尺寸i=0.10 mm的裂纹扩展曲线中疲劳寿命与试验结果最为接近。疲劳寿命主要消耗在疲劳裂纹扩展的初期，微小尺寸裂纹对周边区域受力性能影响很小。

[1] Bruls A. Measurement and interpretation of dynamic loads in bridge. Phase 3: fatigue behaviour of orthotropic steel decks. Common synthesis report[R]. Brussels: Commission of European Communities, 1990: 1−156.

[2] Cuningham J R, Stephens V A, Beales C. Measurement and interpretation of dynamic loads in bridge. Phase 4: fatigue strength of steel bridges. Common Synthesis Report[R]. Brussels: Commission of European Communities, 1995: 1−60

[3] BS EN 1993-1-9-2005 Eurocode 3: Design of Steel Structures -Part1-9: Fatigue[S].

[4] Kolstein M H, Cunninghame J R, Bruls A. Fatigue classification of welded details in orthotropic steel bridge decks[C]// International Conference on Fatigue of welded Components and Structure. Senlis, Paris: Journées Internationales de Printemps, 1996: 15−23

[5] XIAO Zhigang, Yamada K, Inoue J, et al. Fatigue crack in longitudinal ribs of steel orthotropic deck[J]. International Journal of Fatigue 2006, 28(4): 409−416.

[6] 唐亮, 黄李骥, 王春生, 等. 正交异性钢桥面板足尺模型疲劳试验[J]. 土木工程学报, 2014, 47(3): 112−122. TANG Liang, HUANG Liji, WANG Chunsheng, et al. Fatigue experimental study of a full-scale steel orthotropic deck model[J]. China Civil Engineering Journal, 2014, 47(3): 112−122.

[7] 李淞泉, 万珊珊, 史永吉等. 大型公路钢箱梁正交异性桥面板工地接头的研究[C]// 第十四届全国桥梁学术会议论文集. 上海: 同济大学出版社, 2000: 91−99. LI Songquan, WAN Shanshan, SHI Yongji, et al. The study of box girder on-site joints for U-ribs in large highway orthotropic steel deck[C]// The Fourteenth National Bridge Essay. Shanghai: Tongji University Press, 2000: 91−99.

[8] 陶晓燕. 大跨度钢桥关键构造细节研究[D]. 北京: 中国铁道科学研究院, 2008: 60−62. TAO Xiaoyan. Research on key structure details of large-span steel bridges[D]. Beijing: China Academy of Railway Sciences, 2008: 60−62

[9] 顾萍, 周聪. 铁路正交异性钢桥面板典型疲劳裂纹寿命估算[J]. 铁道学报, 2012, 34(1): 97−102.

GU Ping, ZHOU Cong. Estimation of fatigue life of typical fatigue cracks of orthotropic steel decks of railway bridges[J]. Journal of the China Railway Society, 2012, 34(1): 97−102.

[10] 朱劲松, 郭耀华. 正交异性钢桥面板疲劳裂纹扩展机理及数理模拟研究[J]. 振动与冲击, 2014, 33(14): 40−47.

ZHU Jingsong, GUO Yaohua. Numerical simulation on fatigue crack growth of orthotropic steel highway bridge deck[J]. Journal of Vibration and Shock, 2014, 33(14): 40−47.

[11] GB/T 714—2008, 桥梁用结构钢[S]. GB/T 714—2008, Structural steel for bridge[S].

[12] TB 10212—2009, 铁路钢桥制造规范[S]. TB 10212—2009, Fabrication code for railway steel bridges[S].

[13] Miner M A. Cumulative damage in fatigue[J]. Journal of Applied Mechanics, 1945, 12(3): 159−164.

[14] American Association of State Highway and Transportation Officials(AASHTO) LRFD—2012, Bridge design specifications[S].

[15] BS EN 1993−2−2006, Eurocode 3: Design of steel structures-Part 2: Steel bridges[S].

[16] Fisher J W. Fatigue and fracture in steel bridges[M]. New York: Wiley and Sons, Inc, 1984: 215−315.

[17] Lawrence K L. ANSYS workbench tutorial release 13[M]. Shawnee, USA: SDC Publications, 2011: 1−100.

[18] 张安哥, 朱成九, 陈梦成. 疲劳、断裂与损伤[M]. 西安: 西安交通大学出版社, 2006: 103−106. ZHANG Ange, ZHU Chengjiu, CHEN Mengcheng. Fatigue, fracture and damage[M]. Xi’an: Xi`an Jiaotong University Press, 2006: 103−106

[19] Harris D O. Probabilistic fracture mechanics. Probabilistic structural mechanics handbook[M]. New York: Springer US, 1995: 106−145.

[20] Righiniotis T D, Chryssanthopoulos M K. Probabilistic fatigue analysis under constant amplitude loading[J]. Journal of Constructional Steel Research, 2003, 59(7): 867−886.

[21] Nguyen H T, Chu Q T, Kim S E. Fatigue analysis of a pre-fabricated orthotropic steel deck for light-weight vehicles[J]. Journal of Constructional Steel Research, 2011, 67(4): 647−655.

[22] JSSC—1993, Fatigue design recommendations for steel structures and commentary[S].

(编辑 罗金花)

Fatigue life prediction of weld connection in longitudinal ribs of steel orthotropic decks

CHEN Shiming1, LU Yun1, ZHOU Cong2, GU Ping1

(1. College of Civil Engineering, Tongji University, Shanghai 200092, China;2. Department of Mechanical Engineering, University of Canterbury, Christchurch 8140, New Zealand)

Based on detailing of railway bridges, two full scale steel orthotropic decks with butt welds in the longitudinal ribs were designed and fabricated. Then static and fatigue tests (FE) were conducted. Based on the test results, the FE model of the decks was established and the analytic computation was carried out. The FE results were found in agreement with the fatigue tests results. The second-level models with consideration of pre-existing semi-elliptic crack were developed using the sub-modeling technique and singular element to simulate the stress field of the crack front. The stress intensity factors of different initial crack depths in the butt welds of the longitudinal ribs were obtained by displacement extrapolation. Based on reasonable determination of the initial crack depth, the crack propagation was simulated and the fatigue life was predicted by numerical integration of the Paris formula. The results explained how the crack initiated and grew. It is suggested that fatigue detailing of the butt-weld in longitudinal ribs of the steel orthotropic decks be designed in accordance with detailing grade 71 of EC3, or with the detailing IX of the Chinese Design Code of the Steel Railway Bridge.

steel orthotropic decks; fatigue tests; fatigue life; stress intensity factor; sub-modeling technique

10.11817/j.issn.1672-7207.2015.09.040

U24

A

1672−7207(2015)09−3461−07

2014−11−24；

2015−02−07

国家重点基础研究发展计划(973计划)项目(2013CB036303) (Project(2013CB036303) supported by the National Basic Research Development Program (973 Program) of China)

陈世鸣，博士，教授，从事钢结构，组合结构研究；E-mail: chensm@tongji.edu.cn