致密砂岩凝析气藏启动压力梯度

田巍，朱维耀，朱华银，张雪龄，安来志，杜珊



致密砂岩凝析气藏启动压力梯度

田巍1，朱维耀1，朱华银2，张雪龄3，安来志2，杜珊4

(1. 北京科技大学土木与环境工程学院，北京，100083；2. 中国石油勘探开发研究院廊坊分院，河北廊坊，065007；3.郑州轻工业学院能源与动力工程学院，河南郑州，450002；4. 华北油田勘探开发研究院，河北任丘，062552)

为研究致密砂岩凝析气藏启动压力梯度，在原有气泡法流程基础上增设高线性压差传感器，并通过给出一定的平衡时间解决压力传递缓慢的问题，利用回压控制衰竭速度，设计测定凝析气藏启动压力梯度的实验流程，并在精确模拟地层条件下进行室内研究。研究结果表明：所模拟凝析气藏3个区域的启动压力梯度都随着渗透率的增加先急剧降低而后降低的速度放缓，随着渗透率倒数的增加而线性增加，模拟Ⅰ区启动压力梯度最高，约为模拟Ⅲ区启动压力梯度的9.2倍，模拟Ⅱ区启动压力梯度约为模拟Ⅲ区的3.5倍；在影响启动压力梯度的各因素中，含液饱和度和主流喉道半径的影响最大，其次是微裂缝；润湿性主要影响Ⅱ区和Ⅲ区，对Ⅰ区影响极小，对于围压和温度的影响可以通过精确模拟地层条件来消除。

凝析气藏；启动压力梯度；临界流动压力；露点压力；有效围压；液锁效应；含液饱和度

凝析气藏是在原始温度和压力下以气体形式存在的特殊油气藏，当地层压力降到低于露点压力时将会发生反凝析现象，其开发开采有很大难度，而致密砂岩凝析气藏的开采难度更大；开采一般的中高渗透率的储层时，常不考虑启动压力梯度，但致密砂岩储层由于具有岩性致密、毛细管压力高、易发生严重液锁，并常伴有微裂缝发育等特点，其开发和开采就要考虑启动压力梯度的存在。20世纪30年代，美国首先发现凝析气藏，之后很多国家相继发现该类气藏，相关的研究也逐步展开。对于常规气藏启动压力梯度研 究[1−5]较多，其方法主要归结为线性回归法和气泡法2类。线性回归法是通过实验点回归拟合求取启动压力梯度，操作较复杂，不适于有反凝析液析出的气藏的测定；气泡法是测定流体动用瞬间的压力，操作简便、适用范围广，在改进后可以用于凝析气藏启动压力梯度的测定。目前，对于致密砂岩凝析气藏启动压力梯度的研究较少，本文基于气泡法，设计适于测定凝析气藏启动压力梯度的流程和方法，并针对致密砂岩凝析气藏进行实验研究。

1 实验部分

1.1 原理

保持实验温度恒定，当孔隙中充满流体时，驱替压差从低逐渐升高，在某一压差下流体克服岩心中各种阻力后进入孔道，并占据孔道空间体积，由于压力传递作用，流体开始移动，若忽略孔隙中流体的压缩，则在岩心出口端面就会有流体被驱出，使出口管段细管中的气体被挤压在出口产生气泡，考虑到可能会由于压力传递缓慢的问题，为此，关闭夹持器进口阀，直到岩心进出口压力48 h恒定不变，此时进出口压差值即为岩心启动压力。

1.2 设备及流程

实验流程主要包括气体供气与调压系统、岩心驱替与收集装置、围压和回压控制设备、数据采集系统、温度控制系统等5部分，由实验室根据需要进行组装，如图1所示。

在供气系统中，泵的主要作用是通过中间容器为气体加压，注入泵根据实验需要可以设置为恒定流量或恒定压力模式，泵流量为0.01~50.00 mL/min(压力不大于70 MPa)，精度为±0.3%；为了模拟地层应力特征，实验采用三轴岩心夹持器；围压系统使用高精度多级柱塞驱替泵(Teledyne isco100−DX)控制；回压采用美国岩心公司生产的BP−100空气弹簧回压阀，并采用高精度多级柱塞驱替泵控制回压阀。压力测定采用DXD高精度数字压力传感器，同时采用高线性压差传感器(型号为validyne) 来精确采集岩心两端压力差；使用Auto-floodTM(AFS300TM)驱替评价系统进行数据采集并进行数据分析；整套装置置于恒温箱中，恒温箱可调温度范围为0~180 ℃。

1—三轴岩心夹持器；2—注入泵；3—高压氮气瓶；4—模拟气体瓶；5—调压阀；6—流量收集装置；7—回压阀；8—上游压力传感器；9—下游压力传感器；10—压差传感器；11—中间容器

1.3 步骤

按照凝析气藏衰竭开采过程中的压力和流体状态变化，依据距离采出井的远近，将1口采出井的整个波及范围分为3个区域：Ⅲ区为远井区，孔隙压力高于露点压力，存在气、水2相，为束缚水下的气体单相渗流；Ⅱ区为过渡区，压力介于露点压力和临界流动压力之间，存在油气水3相，但油、水不参与流动；Ⅰ区为近井区，压力低于临界流动压力，流动为束缚水状态下的油、气两相渗流。

实验步骤如下：1) 将岩心烘干48 h，测定岩心的长度、直径、质量及气测渗透率，将岩心抽真空饱和标准盐水，称质量并计算有效孔隙度；2) 将岩心装入岩心夹持器，以1 MPa为步长以20 min为间隔缓慢施加围压，当加到实际地层上覆压力后停止施加，而后保持恒定，将实验温度升至60 ℃，接通流程，对仪 器初始值调零，使用氮气驱替岩心至含水不再变化；3) 在中间容器中充满模拟气体并加压至原始地层压力，并设置回压为地层压力，打开岩心夹持器进口阀，对岩心通模拟气体30 min，置换出岩心中的氮气，关闭进气阀，分别将回压缓慢下调并降至露点压力、临界流动压力和井底流压，并保持稳定，观察出口端产气情况，直至出口12 h不产气为止；4) 将夹持器出口管段细管出口置于收集装置液面下，打开充满高压氮气的中间容器出口，而后打开夹持器进气阀，调节调压阀缓慢升压；5) 观察在液面下的出口，直到有第1个气泡冒出，关闭岩心夹持器进口阀，静置上下游压力数据变化，直到压力48 h稳定不变，此时，若步骤3)中回压降至露点压力，则高线性压差传感器数据为Ⅲ区启动压力；如步骤3)中回压降至临界流动压力，则高线性压差传感器数据为Ⅱ区启动压力；如步骤3)中回压降至井底流压，则高线性压差传感器数据为Ⅰ区启动压力。

在测定完模拟Ⅲ区启动压力，转测模拟Ⅱ区、模拟Ⅰ区的启动压力时，每次都要重新对岩心进行充注模拟气体。在模拟Ⅱ区、Ⅰ区时，当回压调至临界流动压力(井底流压)时，要待上游压力衰竭至露点压力(临界流动压力)后，再按照上述方法测定启动压力。

2 实验结果与分析

实验选用吐哈油田同一层位岩性特征相同的致密岩心，岩心基础数据如表1所示，饱和盐水矿化度为80 g/L。实验按照研究区块某采出井初始井流物PVT测试数据配制模拟气体，地层压力为40.34 MPa，露点压力为35.80 MPa，临界流动压力为31.70 MPa，井底压力为22.50 MPa。实验精确模拟地层条件，通过回压阀控制衰竭速度，并以回压来模拟不同的区域。

图2所示为各区启动压力梯度与渗透率的关系曲线。从图2可知：随着渗透率的增加启动压力梯度减小，在渗透率较小时，随着渗透率的增加，启动压力梯度急剧降低，当渗透率超过一定值后，随着渗透率的增加，启动压力梯度减小幅度越来越小，如Ⅱ区当渗透率从0.007 7×10−3μm2增加到0.064 9×10−3μm2再增加到0.693 1×10−3μm2时，启动压力梯度下降幅度分别为0.798 8 MPa/m和0.083 6 MPa/m；存在液相区的模拟区域启动压力梯度变化幅度相应较大，如在渗透率从0.007 7×10−3μm2增加到0.064 9×10−3μm2时，模拟Ⅰ区启动压力梯度从2.237 4 MPa/m降低到0.235 2 MPa/m，下降了2.002 2 MPa/m，约为原来的1/10；而在相同的渗透率变化情况下，模拟Ⅲ区启动压力梯度从0.245 7 MPa/m下降到0.041 6 MPa/m，降低了0.204 1 MPa/m，约为原来的1/6，下降幅度比模拟Ⅰ区小。Ⅲ，Ⅱ和Ⅰ区的启动压力梯度和渗透率之间都符合幂函数相关关系，拟合曲线方程如表2所示；将启动压力梯度和渗透率倒数拟合发现两者符合线性递增关系，而且相关性较好，如图3和表2所示，据此可以绘制启动压力梯度和渗透率倒数关系图版，方便查知不同渗透率岩心的启动压力梯度。

表1 实验岩心基础数据

1—远井区(Ⅲ区)；2—过渡区(Ⅱ区)；3—近井区(Ⅰ区)

表2 岩心启动压力梯度与渗透率拟合关系

注：∆为进出口压差，MPa；为渗透率，10−3μm2；为岩心长度，m。

1—远井区(Ⅲ区)；2—过渡区(Ⅱ区)；3—近井区(Ⅰ区)

模拟Ⅲ区的孔隙压力高于35.80 MPa，孔隙中流动流体为纯气相，压力从40.34 MPa逐渐降到 35.80 MPa，压力跨度为4.54 MPa，随着衰竭开采的进行，动用的范围会逐渐扩大。对于一定渗透率的储层其压力梯度在各处都一样，液体饱和度均匀分布，因此，可以认为所测值是Ⅲ区任何地方该渗透率的启动压力梯度；岩心启动压力梯度随着渗透率的增大而减小，这是由于渗透率越大，通过孔隙介质最大孔道中的流体越容易流动，所需的启动压力越小。

模拟Ⅱ区的压力介于35.80 MPa和31.70 MPa之间，有反凝析液析出并滞留在孔隙中，不参与流动；由于反凝析液量逐渐增加，液锁效应的影响越来越明显，使得渗流阻力加大，启动压力梯度也相应增加；距离采出井越近，液体饱和度越大，直至液体饱和度达到临界流动饱和度，而后再增加的反凝析液为可动流体部分，由于设置的回压为临界流动压力，因此实验所测值为Ⅱ区靠近临界流动压力点处的启动压力梯度，是Ⅱ区该渗透率下最大的启动压力梯度，同时还可以通过设置回压为35.80 MPa和31.70 MPa之间的任何值来测定该压力点下对应渗透率岩石的启动压力梯度。

模拟Ⅰ区的压力介于临界流动压力31.70 MPa和井底压力22.50 MPa之间，孔隙中反凝析液和凝析气共同流动，距离采出井越近，反凝析液聚集越多，含反凝析液饱和度越大。对于气体来说，反凝析液饱和度的增加相应加剧了液锁效应的影响，使气体的有效渗透率大幅降低，这就要求开采过程中保持足够的压差；由于启动压力梯度与渗透率之间存在良好的乘幂关系，启动压力梯度随着渗透率的降低呈递增趋势，当渗透率降低到一定数值后，启动压力梯度呈剧烈变化趋势，由此说明当渗透率降低到一定数值后，启动压力梯度对凝析气藏开发带来较大影响。

对比3个模拟区的启动压力梯度可以发现：Ⅲ区最小，Ⅰ区最大，气液两相启动压力梯度要高于气体单相启动压力梯度；为了找出3个区域启动压力梯度之间的关系，如图4所示，将Ⅱ区、Ⅰ区对Ⅲ区过原点线性回归拟合方程为：

1—过渡区(Ⅱ区)；2—近井区(Ⅰ区)

由式(1)和式(2)可以看出：Ⅰ区启动压力梯度约为Ⅲ区的9.2倍，Ⅱ区启动压力梯度约为Ⅲ区的3.5倍。在以后的室内研究中，可以通过本文的方法测得最容易测定区域的启动压力梯度，再通过上述拟合关系很方便地计算出其他区域的启动压力梯度。

由于岩心长度的限制，本实验只能模拟其中某个区域微段的流动状态，由于实验选取的都是特殊压力点，因此本研究对现场具有参考价值。

3 启动压力梯度影响因素分析

3.1 围压和温度

文献[6−10]研究了围压和温度对气体渗透率的影响，对于实际地层，上覆压力的变化会引起储层有效应力的变化[11−12]，进而影响各相的有效渗透率，温度的增加会引起孔隙中液体和气体黏度的变化以及黏土的膨胀。

图5所示为渗透率0.064 3×10−3μm2岩心启动压力梯度变化曲线。从图5可知：在温度恒定的情况 下，启动压力梯度随着有效围压的增加逐渐增加。启动压力梯度在有效围压为0~10 MPa/m的范围内随有效围压的增加而大幅度增加，当有效围压提高至 10 MPa/m以上，启动压力梯度变化幅度越来越小。在实验温度为60 ℃下，当有效围压从3 MPa提升到 7 MPa和从11 MPa提升到15 MPa变化时，启动压力梯度分别提高了0.008 4 MPa/m和0.001 1 MPa/m，有效围压从11 MPa提升到15 MPa增加的幅度比有效围压从3 MPa提升到7 MPa的增加幅度低。在有效围压恒定的情况下，启动压力梯度随着温度的升高而降低。在有效围压为7 MPa时，实验温度从30 ℃上升到80 ℃，启动压力梯度从0.038 2 MPa/m降到 0.035 2 MPa/m。

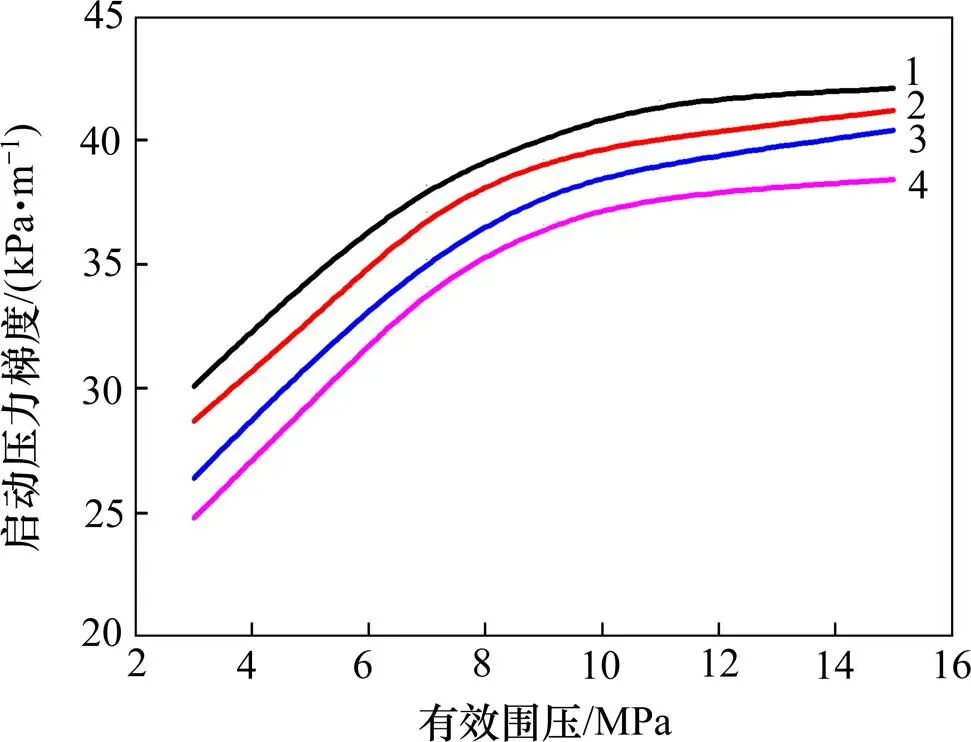
温度/℃：1—30；2—60；3—80；4—100

从图5分析可知：有效围压对启动压力梯度的影响与岩石颗粒受压变形有关，岩石受到有效应力的增加，导致岩石颗粒间受挤压，发生拟塑性变形，孔隙体积和喉道半径随之减小；随着有效应力的继续增大，岩石颗粒受压发生弹性形变，但此时孔喉半径的减小幅度要比拟塑性变形阶段的小。岩石受压发生应力敏感，孔喉减小，渗流阻力增大，渗流效果变差。

研究[9]表明：温度的增加一方面会引起束缚水的蒸发和岩石结晶水的散失；另一方面，引起气体黏度增加；而实际宏观效果是2个方面综合作用的结果，而且这2个方面的作用互相削弱。束缚水的蒸发和岩石结晶水的散失引起的渗流效果的变化要比气体黏度增加产生的变化大，所以，岩石的渗流效果略微变好，渗流阻力有所降低。

实际气藏衰竭开采过程中，孔隙压力逐渐降低，储层有效应力增加，物性变差，因此，应合理控制凝析气藏开采速度。测定启动压力梯度时要严格还原地层条件，即保持上覆压力、回压、温度等条件与实际地层一致，这样测得结果才有实际参考价值。

3.2 润湿性

润湿性的不同会引起岩石束缚水的差异，亲水岩石所含的束缚水偏高，渗流阻力也大，水锁效应相对较明显，启动压力梯度也相应较大。对于凝析气藏，远井区孔隙中含束缚水和可动气体，岩石束缚水饱和度越大，发生水锁效应的可能也越大[13]，有效渗透率下降的也越多，因此，亲水性岩石不利于气体的采出。对于过渡区，孔隙中流动只有气相，但是，反凝析液量逐渐增加，液锁效应越来越明显，渗流阻力变大；因此，在过渡区和远井区，亲水岩石的启动压力梯度要高于疏水岩石启动压力梯度。在近井区，亲水岩石束缚水加残余油饱和度之和与疏水岩石几乎相当，因此，润湿性的影响并不明显。

3.3 含液饱和度

不同岩石含液饱和度下的启动压力梯度如图6所示。从图6可知：启动压力梯度与含液饱和度之间呈现非线性关系，渗透率为0.064 9×10−3μm2的岩心，在含液饱和度从40%上升到55%再上升到70%时，对应启动压力梯度增加幅度分别为0.069 9 MPa/m和0.031 6 MPa/m，含液饱和度从40%上升到55%的启动压力梯度变化幅度大于含液饱和度从55%上升到70%的启动压力梯度，渗透率越低的岩心变化越明显；在渗透率从0.028 4×10−3μm2增加到0.064 9×10−3μm2再增加到0.112 2×10−3μm2情况下，当含液饱和度为50%时，启动压力梯度变化幅分别为0.013 2 MPa/m和0.013 6 MPa/m，当含液饱和度为55%时对应启动压力梯度变化幅度分别为0.021 2 MPa/m和0.015 3 MPa/m。可见，启动压力梯度随含液饱和度的增加而增加，且增加的趋势趋于平缓；在相同含水饱和度情况下，渗透率越高的岩石的启动压力梯度越小(见图6)，曲线间距随着含液饱和度增加而变大。

渗透率/10−3 μm2：1—0.028 4；2—0.064 9；3—0.112 2

熊昕东等[13]分析认为：孔隙所含液体从束缚水开始增加，起初增加的反凝析液不参与流动，但却加剧了液锁效应的危害；孔隙中的含液饱和度与束缚水饱和度加残余油饱和度之和的差值越大，不利的相对渗透率效应就越明显。因此，在较低含液饱和度下，启动压力梯度变化的幅度较大，当含液饱和度超过了束缚水加残余油饱和度之和之后，启动压力梯度的变化就变得相对平缓。在相同的含液情况下，渗透率小的岩石比渗透率高的岩石的可动用流体要少，随着含液饱和度的增加，较低渗透率岩石启动压力梯度增加的幅度也比稍高渗透率的增加幅度大。

3.4 主流喉道半径

岩石主流喉道半径不同，启动压力梯度也不同；启动压力梯度随主流喉道半径的增加先是急剧减小而后降低的速度放缓，如图7所示。从图7可见：对于Ⅰ区，当主流喉道半径从0.211 µm增加到0.642 µm再增加到1.698 µm时，启动压力梯度从2.237 4 MPa/m降到0.235 2 MPa/m再降低到0.036 2 MPa/m，下降幅度分别为2.002 2 MPa/m和0.199 0 MPa/m；对于Ⅱ区，在相同主流喉道半径变化情况下，启动压力梯度下降幅度分别为0.798 8 MPa/m和0.083 7 MPa/m；结果表明：存在可动液相的区域启动压力梯度下降幅度较大。主流喉道半径是储层物性特征的最重要的一个物理参数，因此，主流喉道半径是决定启动压力梯度的重要因素[14]。

1—远井区(Ⅲ区)；2—过渡区(Ⅱ区)；3—近井区(Ⅰ区)

3.5 微裂缝

致密砂岩岩石中常伴有微裂缝发育[15]，裂缝的存在对启动压力梯度存在影响，当存在与流动方向垂直微裂缝情况下，末端效应导致裂缝边界液体饱和度较高，气体在裂缝中由于圈闭作用被封死，后续流体绕流通过，渗流阻力增加，启动压力梯度变大，当存在与流动方向一致的微裂缝时的情况则刚好相反。通过测定渗透率为0.064 9×10−3μm2的岩心在造非贯穿缝前后(0.223 1×10−3μm2)模拟远井区启动压力梯度的数值变化可知：岩心造缝后，启动压力梯度由 0.041 6 MPa/m降低到0.009 1 MPa/m，降低了 0.032 5 MPa/m；在模拟过渡区域时，启动压力梯度由0.084 7 MPa/m降低到0.028 1 MPa/m，降低了 0.059 9 MPa/m，可见，造缝后气体渗流的流通通道变大，渗流阻力降低，启动压力梯度也相应减小。

4 结论

1) 通过增设高线性压差传感器，并给出一定平衡时间来弥补原气泡法的不足，设计了测定致密砂岩凝析气藏启动压力梯度实验流程和方法。

2) 所测3个区域的启动压力梯度都随着渗透率的增加先急剧降低而后降低速度放缓，随着渗透率倒数的增加而线性增加；Ⅰ区启动压力梯度最高，约为Ⅲ区启动压力梯度的9.2倍；Ⅱ区次之，约为Ⅲ区启动压力梯度的3.5倍。

3) 主流喉道半径和含液流体饱和度对启动压力梯度影响较大；其次是微裂缝，润湿性主要影响Ⅱ区和Ⅲ区，对Ⅰ区影响极小；此外，可以通过精确模拟地层条件来消除围压和温度的影响。

[1] 郭红玉, 苏现波. 煤储层启动压力梯度的实验测定及意义[J]. 天然气工业, 2010, 30(6): 52−55. GUO Hongyu, SU Xianbo. An experimental measurement of the threshold pressure gradient of coal reservoirs and its significance[J]. Natural Gas Industry, 2010, 30(6): 52−55.

[2] 王道成, 李闽, 乔国安, 等. 天然气启动压力梯度实验研究[J].钻采工艺, 2007, 30(5): 53−55.WANG Daocheng, LI Min, QIAO Guoan, et al. Experimental study of gas threshold pressure gradient[J]. Drilling & Production Technology, 2007, 30(5): 53−55.

[3] 胡勇. 气体渗流启动压力实验测试及应用[J]. 天然气工业, 2010, 30(11): 48−50. HU Yong. Experiment and application of threshold pressure for gas flow[J]. Natural Gas Industry, 2010, 30(11): 48−50.

[4] 章星, 杨胜来, 张洁, 等. 致密低渗气藏启动压力梯度实验研究[J]. 特种油气藏, 2011, 18(5): 103−104. ZHANG Xing, YANG Shenglai, ZHANG Jie, et al. Experimental study on threshold pressure gradient of tight and low permeability gas reservoirs[J]. Special Oil & Gas Reservoirs, 2011, 18(5): 103−104.

[5] 王瑞飞, 吕新华, 国殿斌. 高压低渗砂岩油藏储层驱替特征及影响因素[J]. 中南大学学报(自然科学版), 2012, 43(3): 1072−1079. WANG Ruifei, LÜ Xinhua, GUO Dianbin. Displacement characteristics and influencing factors in deep section high pressure and low permeability sandstone reservoir[J]. Journal of Central South University (Science and Technology), 2012, 43(3): 1072−1079

[6] 刘均荣, 秦积舜, 吴晓东. 温度对岩石渗透率影响的试验研究[J]. 中国石油大学学报(自然科学版), 2001, 25(4): 51−53. LIU Junrong, QIN Jishun, WU Xiaodong. Experimental study of relation between temperature and rock permeability[J]. Journal of the University of Petroleum China (Natural Science), 2001, 25(4): 51−53.

[7] 贺玉龙, 杨立中. 温度和有效应力对砂岩渗透率的影响机制研究[J]. 岩石力学与工程学报, 2005, 24(14): 2420−2427. HE Yulong, YANG Lizhong. Mechanism of effects of temperature and effective stress on permeability of sandstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(14): 2420−2427.

[8] Schembre J M, Kovscek A R. Mechanism of formation damage at elevated temperature[J]. Journal of Energy Resources Technology, 2005, 127(3): 171−180.

[9] 梁冰, 高红梅, 兰永伟. 岩石渗透率与温度关系的理论分析和试验研究[J]. 岩石力学与工程学报, 2005, 24(12): 2010−2012. LIANG Bing, GAO Hongmei, LAN Yongwei. Theoretical analysis and experimental study on relation between rock permeability and temperature[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(12): 2010−2012.

[10] Amro M M, Benzagouta M S. Pressure and temperature effect on petrophysical characteristics: carbonate reservoir case[J]. Oil Gas-European Magazine, 2009, 35(2): 74−78.

[11] 刘建军, 刘先贵. 有效应力对低渗透多孔介质孔隙度、渗透率的影响[J]. 地质力学学报, 2001, 7(1): 41−44. LIU Jianjun, LIU Xiangui. The effect of effective pressure on porosity and permeability of low permeability porous media[J]. Journal of Geomechanics, 2001, 7(1): 41−44.

[12] 谷达圣, 鲜学福, 周军平, 等. 有效应力和不同气体对煤的渗透性影响分析[J]. 地下空间与工程学报, 2012, 8(6): 1296−1301. GU Dasheng, XIAN Xuefu, ZHOU Junping, et al. Experiment study of the influence of effective stress and different gases on coal permeability[J]. Chinese Journal of Underground Space and Engineering, 2012, 8(6): 1296−1301.

[13] 熊昕东, 王世泽, 张国东, 等. 新场气田上沙溪庙气藏水锁效应研究[J]. 钻采工艺, 2007, 30(4): 95−98. XIONG Xindong, WANG Shize, ZHANG Guodong, et al. Study on water lock effect in Xinchang Shaxi gas reservoir[J]. Drill & Production Technology, 2007, 30(4): 95−98.

[14] 熊伟, 雷群, 刘先贵, 等. 低渗透油藏拟启动压力梯度[J]. 石油勘探与开发, 2009, 36(2): 232−235. XIONG Wei, LEI Qun, LIU Xiangui, et al. Pseudo threshold pressure gradient to flow for low permeability reservoirs[J]. Petroleum Exploration and Development, 2009, 36(2): 232−235.

[15] 付静, 孙宝江, 于世娜, 等. 裂缝性低渗透油藏渗流规律实验研究[J]. 中国石油大学学报(自然科学版), 2007, 31(3): 81−84. FU Jing, SUN Baojiang, YU Shina, et al. Experimental study on seepage flow law of fractured low permeability reservoir[J]. Journal of China University of Petroleum (Edition of Natural Science), 2007, 31(3): 81−84.

(编辑 罗金花)

Condensate gas reservoir threshold pressure gradient for tight sandstone

TIAN Wei1, ZHU Weiyao1, ZHU Huayin2, ZHANG Xueling3, AN Laizhi2, DU Shan4

(1. School of Civil and Environmental Engineering, University of Science & Technology Beijing, Beijing 100083, China;2. Langfang Branch, PetroChina Research Institute of Petroleum Exploration & Development, Langfang 065007, China;3.School of Energy and Power Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002, China;4. Institute of Exploration and Development, North China Oilfield, Renqiu 062552, China)

In order to study threshold pressure gradient for tight sandstone condensate gas reservoir，based on the original process of Bubble method, high linear differential pressure sensor was added. The pressure was tested accurately by keeping the balance time to solve the slow pressure transmission. Moreover, the rate of collapse was controlled by using back pressure. The experimental process of testing condense gas reservoirs threshold pressure gradient was designed, and the research was carried out under the condition of accurate simulation formation in laboratory. The results show that the condensate gas reservoirs threshold pressure gradients of three areas firstly reduce quickly along with the increase of permeability, and then reduce slowly, and increase linearly with the increase of the reciprocal of permeability. The threshold pressure gradient of area Ⅰ is the highest of the three areas, and that is about 9.2 times of that of area Ⅲ.By contrast, the threshold pressure gradient of area Ⅱ is 3.5 times that of area Ⅲ. Besides, among all the various factors influencing the threshold pressure gradient, the influence of fluid saturation and mainstream throat radius is the largest, followed by the micro-fracture. Wettability mainly affects areaⅡ and Ⅲ, and hardly affects area Ⅰ. The influence of confining pressure and temperature can be eliminated by simulating accurately formation conditions.

condensate gas reservoir; threshold pressure gradient; critical flow pressure; dew-point pressure; effective confining pressure; liquid blocking effect; liquid saturation

10.11817/j.issn.1672-7207.2015.09.034

TE37

A

1672−7207(2015)09−3415−07

2014−11−27；

2015−02−15

国家科技重大专项(2011ZX05051)；国家重点基础研究发展计划(973计划)项目(2013CB228002) (Project(2011ZX05051) Supported by National Science and Technology Major Project; Project(2013CB228002) supported by the National Basic Research Development Program (973 Program) of China)

朱维耀，教授，博士生导师，从事渗流流体力学和油气田开发方面的研究；E-mail: Weiyaook@sina.com