多导联癫痫脑电信号高频振荡特征提取与病灶定位算法
2015-12-21王春生黎清清吴敏王东生杜玉晓
王春生,黎清清,吴敏,王东生,杜玉晓
多导联癫痫脑电信号高频振荡特征提取与病灶定位算法
王春生1,黎清清1,吴敏1,王东生2,杜玉晓3
(1. 中南大学信息科学与工程学院,湖南长沙,410083;2. 中南大学湘雅医院,湖南长沙,410008;3. 广东工业大学自动化学院,广东广州,510006)
针对癫痫脑电信号中识别高频振荡节律困难的问题,提出一种基于Teager能量算子和曲线长度的多导联高频振荡节律(high-frequency oscillations,HFOs)特征提取与病灶定位算法。首先,采用陷波器和FIR数字滤波器对癫痫高频振荡信号进行预处理,其次,利用Teager能量算子和曲线长度对高频振荡节律的特征进行提取。最后,以功率谱为手段进行癫痫病灶定位。实际癫痫高频振荡仿真实验结果验证了该方法的有效性。
癫痫脑电;高频振荡;Teager能量算子;特征提取;癫痫病灶定位
全世界癫痫病的年发病率为(50~70)/10 万。据估计,美国人口的1%~2%患有癫痫;而由世界卫生组织在我国组织的大规模调查报告,我国国内的患病率约为8‰,这意味着国内有1千多万癫痫患者[1−2],其中难治性癫痫为250万人左右。癫痫在神经系统类疾病中已经是仅次于脑血管病的疾病[3],研究癫痫发作过程中的各种异常脑电信号对癫痫的诊断和治疗具有重要意义。目前,对于癫痫脑电信号的研究大都集中在100 Hz以下的频率段。而研究表明,在癫痫发作前后,利用颅内电极进行高采样率采集脑电信号可以发现一种频率段更高的信号,称为高频振荡节律HFOs (high-frequency oscillations),与癫痫发作有着密切关系[4],反映了癫痫发作过程中异常脑电信号的重要特征[5−6],其中,在80~200 Hz频率范围内的高频振荡节律被称为“ripples”,可视为一种正常的高频振荡节律;超过200 Hz的高频振荡信号多被认为是一种病理性的高频振荡节律,与癫痫发作过程中生理变化产生的异常脑电信号有着密切联系,主要包括频率范围为200~600 Hz的快速ripples(FRS)和1.0~2.0 kHz频率范围的VHFO(very high frequency oscillations)[7]。病理性的HFOs和正常的HFOs的主要区别是其发生的部位不同,正常的HFOs不可能发生在齿状回结构中。在癫痫发作时,伴随着HFOs的产生和扩散,当影响到大脑的运动皮层区时,表现为患者的局部运动症状即所谓的临床表现形式。在癫痫发作间期,HFOs具有分布的特异性,在癫痫始发区域从外至内,HFOs发生的频率越来越高,特别是FRS,越靠近癫痫病灶的核心区,记录的FRS频率就越高[8]。在时间上,在癫痫发作间期会有一个HFOs从内至外的扩散过程,从空间上,越靠近癫痫的病灶始发区,记录的FRS频率应该越高。对于VHFO,人们对它的研究起步较晚,而且由于它的频率非常高导致采集更加困难,现在对高频振荡信号的研究还主要集中在ripples和FRS这2种信号。国外学者对高频振荡的分析算法进行了探索性研究。加州大学的研究人员[9]使用12位精度的16通道采样系统采集人体脑内颅内宽频带为0.1~5.0 kHz的脑电信号,利用FFT功率频谱分析后用海明窗(FIR)函数法带通滤波器获得80~200 Hz的频率段,再通过非线性拟合洛仑兹分配从运动电子和视觉干扰信号中提取出高频振荡波。Jose等[10]用12位精度的16通道采样系统采集宽频带1~5 kHz的模拟高频波信号,其采样频率为20 kHz,获取高频信号熵之后,用FIR带通滤波器获得频率为250~600 Hz的带通信号,然后结合希尔伯特变换进行宽带相移获取有用的高频信号。Smart等[11]用脑电图来自动检测癫痫患者颅内的高频振荡,采用1个12位的64通道癫痫检测系统,以200 Hz的采用频率采集0.1~100 Hz宽频带的脑电波,采取1 min/数据段的方式对多个数据段进行高通滤波,再对每一段的数据进行特征提取,进而获取癫痫高频信号。目前,对于高频振荡信号的研究还不成熟,国内外仅有10余家单位研究关于癫痫的高频振荡信号的提取,且采用的方法主要是FFT功率谱分析[9]、FIR滤波[9−10]、定量分析[11]、拉普拉斯变换[12]、小波变换熵[13]、支持向量机[14]和MP算法[15]等,研究成果也仍未用于临床诊断。为此,本文作者针对高频振荡节律识别困难的问题,先对原始数据进行50 Hz倍频陷波,消除工频干扰,提出基于FIR带通滤波器和Teager能量算子的算法来提取高频振荡信号,并结合其功率谱密度分析,通过寻找FRS发生频率最高的导联,实现癫痫病灶始发区的定位,以便于癫痫疾病的治疗。
1 高频振荡特征提取与病灶定位算法
癫痫脑电信号处理过程如图1所示。

图1 结构框图
1.1 癫痫脑电信号的预处理
脑电(electroencephalogram, EEG)是大脑组织中大量的神经元群突触后电流在大脑皮层或头皮表面的综合表现,能够很好地反映脑信息[16]。现代脑科学研究表明,多导的脑电信号蕴含着多种生理现象,按照一定标准放置的多个电极处同步采集的电信号,反映更多的动态信息[17]。因为脑电是通过不同位置的电极测量得到的,所以,这些电极不仅记录了脑内神经元电活动,而且记录了各种干扰信号,如工频干扰、眼球运动、呼吸波干扰和肌电干扰等。
预处理过程中最常用的是对信号进行数字滤波,根据HFOs的频率特点,所需信号的频率段为ripples(80~200 Hz)和FRS(200~600 Hz)。设计有限长脉冲响应滤波器(finite impulse response, FIR)截取相应频率段的信号,消除其他无关信号[18]。
利用MATLAB设计50 Hz倍频工频陷波器,采用窗函数法设计FIR带通滤波器。窗口类型采用汉明窗,滤波器的阶数选择150阶,通频带为80~200 Hz和200~600 Hz。
1.2 高频振荡节律的特征提取
为了进一步确定某段信号是否为HFOs,需要对滤波之后的信号进行特征提取。要从背景信号中获得准确的定量信息。选取类别可分的特征是关键,本文采用Teager能量算子和曲线长度法进行特征提取。Teager能量算子原始的表达式为
可将式(1)进一步推导为连续信号表达式(2)和离散信号表达式(3)[19],Teager能量算子的输出值称为TEO(teager energy operator)值(记为TE)。对于任意连续信号,Teager能量算子的定义式为
对于离散信号,每一个瞬时只需计算连续3个样本数据点就可以得到任意时刻处的信号能量,具有很好的瞬时性。
通过计算几个连续TE的曲线长度可以得到TE的1个阈值,用于去除较低的TE,增强TE的分离效果。曲线长度的定义式为
其中:为连续所取的点数。因为在Teager能量信号的任意能量值点处,前后的横坐标之差为1,因此,连续2点之间的曲线长度可以近似用其纵坐标之差来代替,而又能够很好地控制这一串数据曲线长度所选取的点数。
1.3 高频振荡节律的病灶定位
信号通常以波的形式体现,将波的频谱密度乘以1个适当系数后可得到每单位频率波携带的功率,称为信号的功率谱密度(power spectral density, PSD,记为PS)。
对于不同导联上的癫痫信号,越靠近癫痫病灶位,产生的HFOs频率会更加高,含有高频振荡节律的导联比未含有高频振荡节律的导联上的高频成分要多。对于含有高频振荡信号的导联,其所携带的功率要比未含有高频振荡信号的导联携带功率要大,其PS越大。基于此特点,本文提出高频振荡节律的病灶定位算法。
对于直接法的功率谱估计,当数据长度太大时,谱曲线起伏加剧,若太小,谱的分辨率又不高,则可用Bartlett法进行改进。
Bartlett平均周期图方法是将点的有限长序列分段求周期图再平均,将分成段,每段有个样本,因而。第段样本序列可写成(0≤≤−1, 1≤≤),第段的功率谱密度PS的估计值为
谱估计定义为段功率谱密度PS的平均估计值为
利用Welch法对Bartlett法进行2方面修正:一是选择适当的窗函数,并在周期图计算前直接加进去;二是在分段时,使各段之间有重叠,这样会使方差减小。
2 实验结果分析与癫痫定位应用
本文所用的脑电位信号数据来源于国内某医院,采用的是深入电极采集方式,采样频率为2.0 kHz,采集的导联数为64导联。据第1个病人的脑电位,确定其第3导联对应癫痫病灶位。
首先,利用工频陷波器和FIR数字带通滤波器对脑电位进行预处理。采用的数据源是知道含有HFOs的第3导联癫痫病人的脑电位。原始脑电位信号数据和预处理之后数据对比如图2所示,频谱对比图如图3所示。
从图2可以看出有效信号的幅值集中在−300~300 µV,陷波前后脑电位数据差异很大,经过200~600 Hz带通滤波后,可以看到FRS存在,其幅值为−10~10 µV,说明高频振荡节律具有高频率低幅值的特点。由图3也可以说明50 Hz倍频干扰信号在原始数据中大量存在。

(a) 原始脑电信号数据;(b) 陷波后脑电信号数据;(c) 带通滤波后脑电信号数据

(a) 原始脑电信号数据频谱;(b) 陷波后脑电信号数据频谱;(c) 带通滤波后脑电信号数据频谱
事实上,在对本组脑电位数据的全部64个导联进行80~200 Hz和200~600 Hz带通滤波分析之后发现:80~200 Hz的ripples在许多导联上存在,而明显的200~600 Hz的FRS只是在第3导联上存在,说明FRS能够直接反映癫痫的发作,而ripples与癫痫发作的关系还需进一步研究。
其次,利用Teager能量算子和曲线长度法对高频振荡进行特征提取。计算第3导联的Teager能量算子结果图,如图4所示,而未含有FRS节律的第1导联的Teager能量算子结果如图5所示。
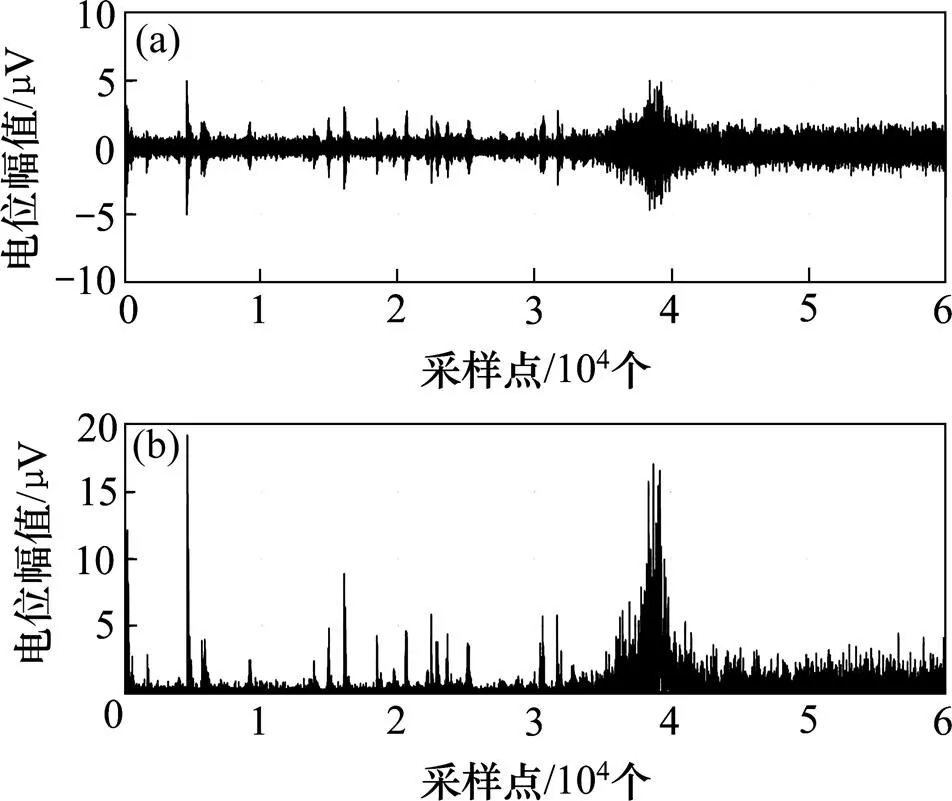
(a) 导联3带通滤波后数据;(b) Teager能量算子数据

(a) 导联1带通滤波后数据;(b) Teager能量算子数据
从图4可以看出:在数据的前4 000个采样点,每个较大的TE对应着原始数据的每个FRS节律,而且FRS表现得越明显,其TE更大;而在4 000以后的采样点的幅值并不比FRS的小,但通过TE计算之后并没有很大TE,说明其频率应该比FRS的低。利用Teager能量算子可以很好地将高频率的FRS特征表现出来。
从图5中也可以看出对于未含有FRS的导联求出的TE分布图与图4中含有FRS导联的TE分布有明显区别,说明Teager能量算子检测FRS存在的有效性。
为了进一步修正TE的空间分离效果,消除低TE对结果的影响,利用曲线长度确定TE阈值,舍弃非FRS的TE。在式(4)中,取为3,计算连续3个点TE的曲线长度,第3导联TE的曲线长度分布如图6所示。
从图6可以看到第3导联的TE主要分布在6以下,加上1个连续3点的曲线长度阈值6,再计算TE,其结果如图7所示。

图6 第3导联电位曲线长度OTE分布图

(a) 导联3带通滤波后脑电数据;(b) 导联3的TE;(c) 导联3加阈值的TE
图7带阈值第3导联Teager能量算子
Fig. 7 Teager energy operator of the 3rd electrode with threshold
从图7可以看出:在结果中加入阈值之后可以更好地增强TEO在特征空间的分离结果,使结果更加清晰、明了。其PSD谱对比图如图8所示。
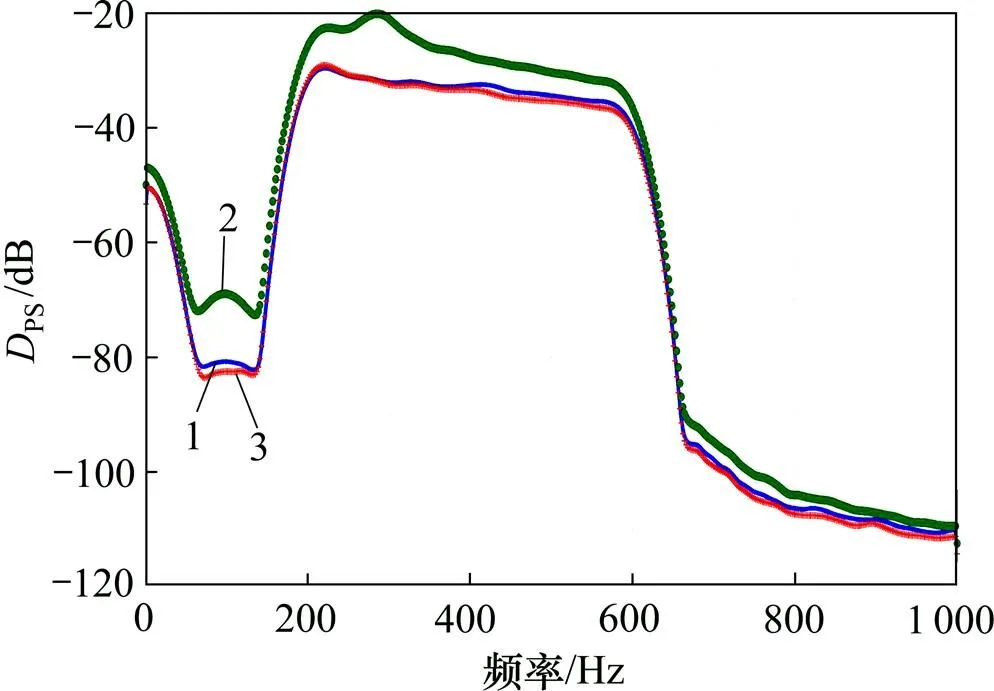
1—导联1;2—导联3;3—导联38
从图8可以看出:含有HFOs导联的PS高频段比其他导联的PS大。根据不同导联的PS进行癫痫病灶位的初步判读原则,PS最大的导联认为是含有大量HFOs的导联,其对应的脑部位置就是癫痫病灶位置,因此,可以认为PS大的导联对应脑部的癫痫病灶位。
为了验证方法的有效性,对第2个病人的癫痫数据进行处理(处理之前不知道癫痫病灶位所对应的导联)。结果表明:第2个病人的疑似癫痫病灶位导联分别为第42导联、第50导联、第55导联、第60导联和第61导联。为了保证结果的清晰度,给出其中3个导联的结果,其带通滤波之后的结果见图9。

(a) 导联42;(b) 导联50;(c) 导联55
从图9可以看出:第2个病人的癫痫数据不像第1个病人的癫痫数据那样好判读,在第2个病人5个导联上同时检测到FRS,说明FRS扩散到某一区域比较快,被几个导联同时检测到。其中细微的差别是第55导联的值更加大。第2个病人癫痫数据对应的TE如图10所示,PS对比图如图11所示。

(a) 导联42 ;(b) 导联50 ;(c) 导联55

1—导联42;2—导联50;3—导联55;4—导联60;5—导联61
从图10可以看出:对于检测到的FRS,对应的第55导联的TE比其他导联的TE要大得多。通过与图11所示PS对比可以看出:第55导联上的高频成分最多,表明第2个病人的癫痫病灶始发区为第55导联。该结果与医生所诊断的结果一致,证明了该方法的有效性。
3 结论
1) 对真实脑电癫痫数据的工频陷波、FIR带通滤波进行预处理,基于HFOs 的能量和频率特征,利用Teager能量算子和曲线长度法对高频振荡节律特征进行提取,并结合功率谱对癫痫病灶进行初步定位。
2) Teager能量算子可以成功地检测到高频振荡节律特别是FRS,在此基础上,选择疑似含有HFOs的导联计算其PSD进行癫痫病灶位判读。
3) 实际癫痫高频振荡数据仿真实验结果验证了该方法的有效性。
[1] 季伟华, 苗玲. 抗癫痫药物与认知障碍[J]. 中国现代神经疾病杂志, 2008, 8(6): 572−576. JI Weihua, MIAO Ling. Antiepileptic drugs and cognitive impairment[J]. Chinese Journal of Contemporary Neurology and Neurosurgery, 2008, 8(6): 572−576.
[2] 韩仲谋, 张晓琴. 癫痫致痫灶、病理灶的定位研究进展[J]. 国际神经病学神经外科学杂志, 2010, 37(5): 461−465. HAN Zhongmou, ZHANG Xiaoqin. The study progress of epilepsy epileptic foci[J]. Journal of International Neurology and Neurosurgery, 2010, 37(5): 461−465.
[3] 娄平阳, 张建国. 难治性癫痫的术前评估及手术治疗[J]. 立体定向和功能性神经外科杂志, 2008, 21(3): 176−181. LOU Pingyang, ZHANG Jianguo. Preoperative assessment of refractory epilepsy and surgery[J]. Chinese Journal of Stereotactic and Functional Neurosurgery, 2008, 21(3): 176−181.
[4] Worrell G A, Parish L, Cranstoun S D, et al. High-frequency oscillations and seizure generation in neocortical epilepsy[J]. Brain, 2004, 127(7): 1496−1506.
[5] Bragin A, Mody I, Wilson C L. Local generation of fast ripples in epileptic brain[J]. The Journal of Neuroscience, 2002, 22(5): 2012−2021.
[6] Bragin A, Wilson C, Engel J. Chronic epileptogenesis requires development of a network of pathologically interconnected neuron clusters: A hypothesis[J]. Epilepsia, 2000, 41(6): 144−152.
[7] 董轩萁, 彭毓莠, 伍炯星. 高频振荡节律的起源、定位及其意义[J]. 生理科学进展, 2012, 43(3): 235−237. DONG Xuanji, PENG Yuxiu, WU Jiongxing. The high-frequency oscillation rhythm's origin, positioning and significance[J]. Progress in Physiological Sciences, 2012, 43(3): 235−237.
[8] Milan B, Jose H, Pavel J, et al. Interictal high-frequency oscillations indicate seizure onset zone in patients with focal cortical dysplasia[J]. Epilepsy Research, 2010, 90(1/2): 28−32.
[9] Staba R J, Wilson C L, Bragin A, et al. Quantitative analysis of high-frequency oscillations (80−500 Hz) recorded in human epileptic hippocampus and entorhinal cortex[J]. Journal of Neurophysiology, 2002, 88(4): 1743−1752.
[10] Jose I, Guglielmo F, Elena C. Emergent dynamics of fast ripples in the epileptic hippocampus[J]. Neuroscience, 2010, 30(48): 16249−16261.
[11] Smart O L, Worrell G A, Vachtsevanos G J, et al. Automatic detection of high frequency epileptiform oscillations from intracranial EEG recordings of patients with neocortical epilepsy[C]// 2005 IEEE Regions and IEEE Denver Section Technical, Professional and Student Development Workshop. Boulder, USA, 2005: 53−58.
[12] Makeyev O, Liu X, Wang L L, et al. Feasibility of recording high frequency oscillations with tripolar concentric ring electrodes during pentylenetetrazole-induced seizures in rats[C]// 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). San Diego, CA, USA, 2012: 4599−4602.
[13] HU Zhikun, XU Fei, GUI Weihua, et al. Wavelet matrix transform for time-series similarity measurement[J]. Journal of Central South University of Technology, 2009, 16(5): 0802−0806.
[14] HE Yongxiu, HE Haiying, WANG Yuejin, et al. Forecasting model of residential load based on general regression neural network and PSO-Bayes least squares support vector machine[J]. Journal of Central South University, 2011, 18(4): 1184−1192.
[15] Chaibi S, Bouet R, Jung J, et al. Development of Matlab-based graphical user interface(GUI) for detection of high frequency oscillations(HFOs) in epileptic patients[C]// 2012 IEEE International Conference on Emerging Signal Processing Applications. Las Vegas, NV, USA, 2012: 56−62.
[16] Yusuf U K, Jean G. High frequency oscillations in intracranial recordings of epileptic patients[C]// International Conference on Multimedia, Signal Processing and Communication Technologies. Aligarh, India, 2011: 126−129.
[17] Boashash B, Carson H, Mesbah M. Detection of seizures in newborns using time-frequency analysis of EEG signals[C]// Proceedings of the Tenth IEEE Workshop on Statistical Signal and Array Processing. Pocono Manor, PA, USA, 2000: 564−568.
[18] Biller S, Simon L, Fiedler P, et al. High frequency oscillations evoked by peripheral magnetic stimulation[C]// Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS). Boston, MA, 2011: 1149−1152.
[19] Kaiser J F. On a simple algorithm to calculate the ‘energy’ of a signal[C]// Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. Albuquerque, New Mexico, USA, 1990: 381−384.
(编辑 陈灿华)
High frequency oscillation feature extraction of multi-lead EEG epilepsy and lesion localization algorithm
WANG Chunsheng1, LI Qingqing1, WU Min1, WANG Dongsheng2, DU Yuxiao3
(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;2. Xiangya Hospital, Central South University, Changsha 410008, China;3. School of Automation, Guangdong University of Technology, Guangzhou 510006, China)
Considering that it is difficult to identify the high frequency oscillation issues in epileptic electroencephalogram (EEG), a multi-lead high frequency oscillation feature extraction and lesion localization algorithm was proposed based on Teager energy operator and curve length. Firstly, a notch filter and FIR digital filters were adopted to preprocess the high frequency oscillation of epilepsy. Secondly, teager energy operator and curve length were used to extract features in high-frequency oscillation. Finally, power spectrum was taken as a means of initial positioning for epileptic foci. The experiment results of actual epilepsy high frequency oscillation data simulation verify the feasibility of the method.
eileptic electroencephalogram; high frequency oscillation; Teager energy operator; feature extraction; epilepsy positioning
10.11817/j.issn.1672-7207.2015.09.020
TP273
A
1672−7207(2015)09−3302−07
2014−10−22;
2014−12−26
国家自然科学基金资助项目(61573381) (Project(61573381) supported by the National Natural Science Foundation of China)
黎清清,博士,从事脑电信号处理研究;E-mail: liqingqing@csu.edu.cn
